Simultaneous imputation and disease classification in incomplete medical datasets using Multigraph Geometric Matrix Completion (MGMC)

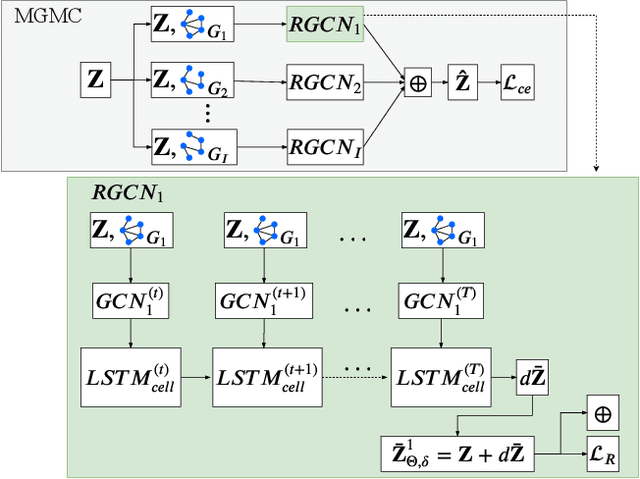
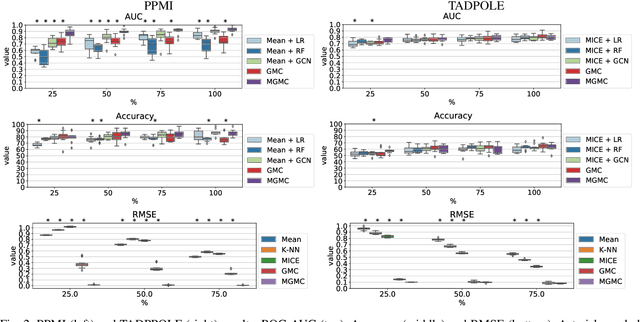
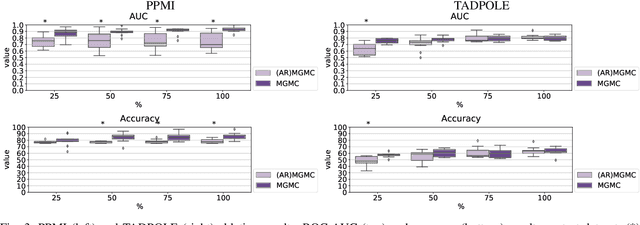
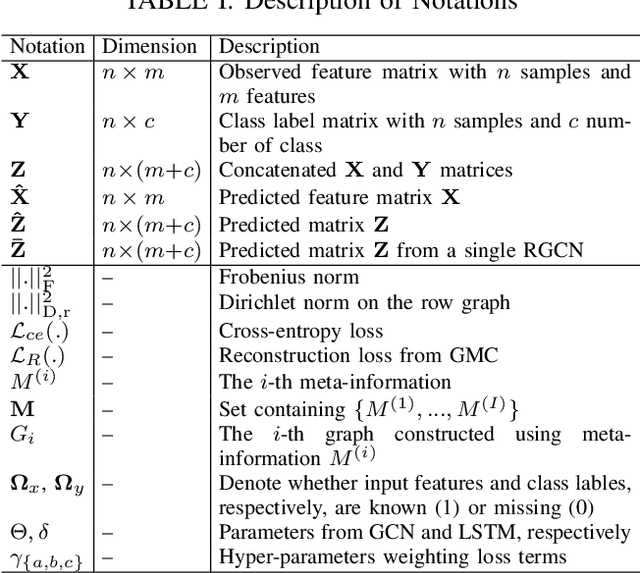
Large-scale population-based studies in medicine are a key resource towards better diagnosis, monitoring, and treatment of diseases. They also serve as enablers of clinical decision support systems, in particular Computer Aided Diagnosis (CADx) using machine learning (ML). Numerous ML approaches for CADx have been proposed in literature. However, these approaches assume full data availability, which is not always feasible in clinical data. To account for missing data, incomplete data samples are either removed or imputed, which could lead to data bias and may negatively affect classification performance. As a solution, we propose an end-to-end learning of imputation and disease prediction of incomplete medical datasets via Multigraph Geometric Matrix Completion (MGMC). MGMC uses multiple recurrent graph convolutional networks, where each graph represents an independent population model based on a key clinical meta-feature like age, sex, or cognitive function. Graph signal aggregation from local patient neighborhoods, combined with multigraph signal fusion via self-attention, has a regularizing effect on both matrix reconstruction and classification performance. Our proposed approach is able to impute class relevant features as well as perform accurate classification on two publicly available medical datasets. We empirically show the superiority of our proposed approach in terms of classification and imputation performance when compared with state-of-the-art approaches. MGMC enables disease prediction in multimodal and incomplete medical datasets. These findings could serve as baseline for future CADx approaches which utilize incomplete datasets.

Peri-Diagnostic Decision Support Through Cost-Efficient Feature Acquisition at Test-Time

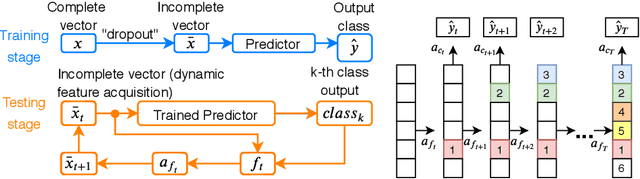
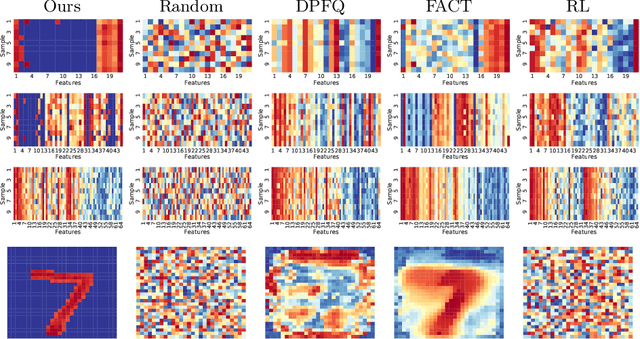
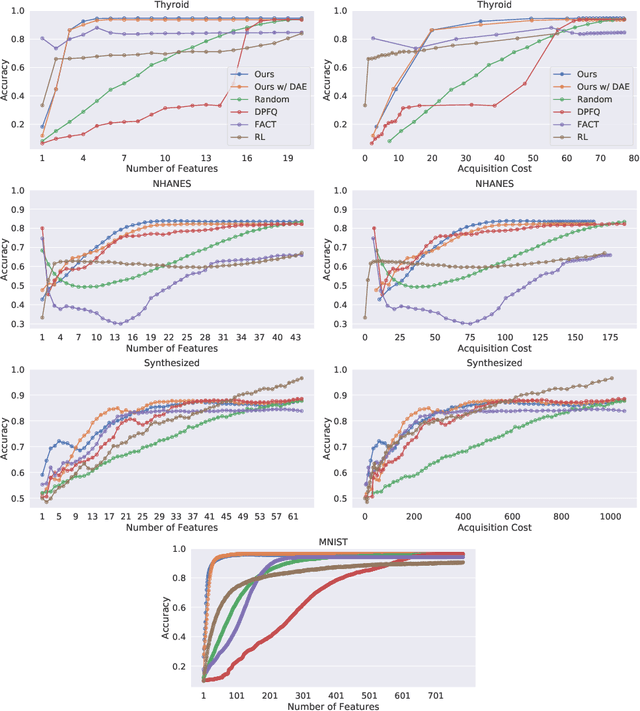
Computer-aided diagnosis (CADx) algorithms in medicine provide patient-specific decision support for physicians. These algorithms are usually applied after full acquisition of high-dimensional multimodal examination data, and often assume feature-completeness. This, however, is rarely the case due to examination costs, invasiveness, or a lack of indication. A sub-problem in CADx, which to our knowledge has received very little attention among the CADx community so far, is to guide the physician during the entire peri-diagnostic workflow, including the acquisition stage. We model the following question, asked from a physician's perspective: ''Given the evidence collected so far, which examination should I perform next, in order to achieve the most accurate and efficient diagnostic prediction?''. In this work, we propose a novel approach which is enticingly simple: use dropout at the input layer, and integrated gradients of the trained network at test-time to attribute feature importance dynamically. We validate and explain the effectiveness of our proposed approach using two public medical and two synthetic datasets. Results show that our proposed approach is more cost- and feature-efficient than prior approaches and achieves a higher overall accuracy. This directly translates to less unnecessary examinations for patients, and a quicker, less costly and more accurate decision support for the physician.

Multi-modal Graph Fusion for Inductive Disease Classification in Incomplete Datasets

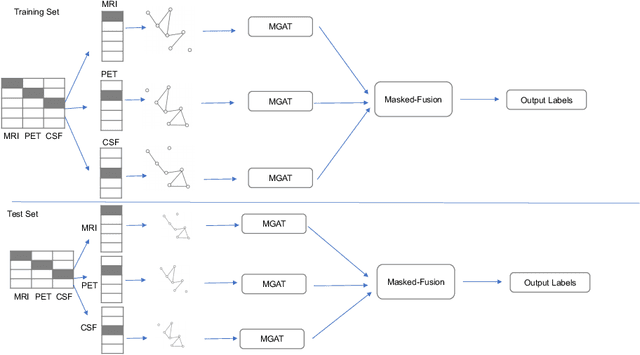
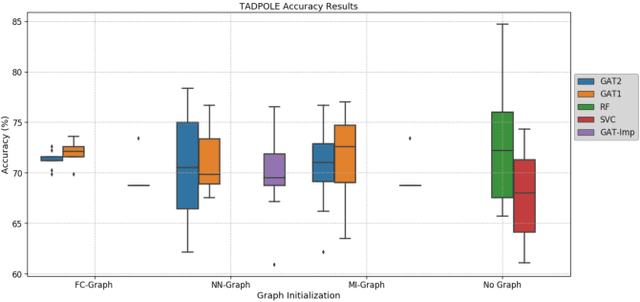
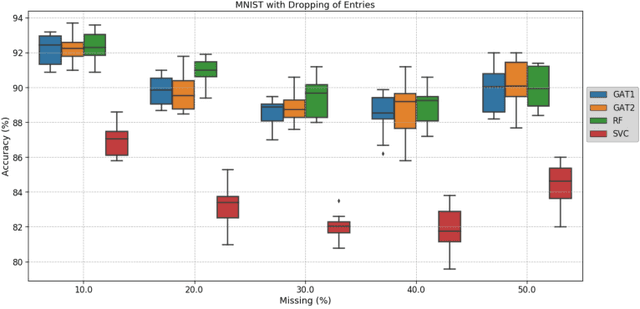
Clinical diagnostic decision making and population-based studies often rely on multi-modal data which is noisy and incomplete. Recently, several works proposed geometric deep learning approaches to solve disease classification, by modeling patients as nodes in a graph, along with graph signal processing of multi-modal features. Many of these approaches are limited by assuming modality- and feature-completeness, and by transductive inference, which requires re-training of the entire model for each new test sample. In this work, we propose a novel inductive graph-based approach that can generalize to out-of-sample patients, despite missing features from entire modalities per patient. We propose multi-modal graph fusion which is trained end-to-end towards node-level classification. We demonstrate the fundamental working principle of this method on a simplified MNIST toy dataset. In experiments on medical data, our method outperforms single static graph approach in multi-modal disease classification.

Adaptive image-feature learning for disease classification using inductive graph networks

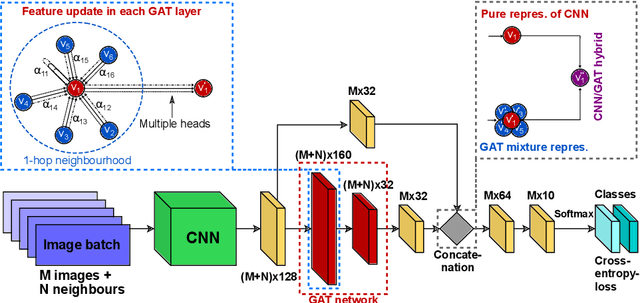
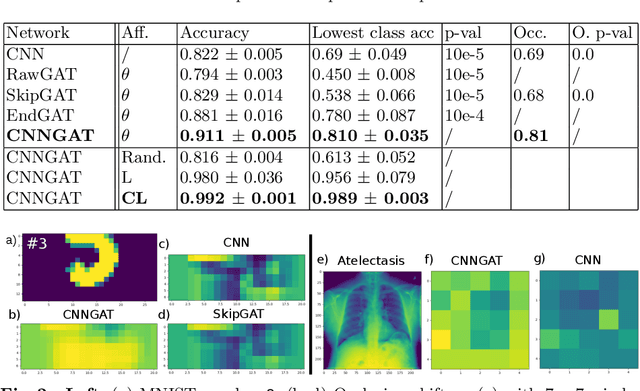
Recently, Geometric Deep Learning (GDL) has been introduced as a novel and versatile framework for computer-aided disease classification. GDL uses patient meta-information such as age and gender to model patient cohort relations in a graph structure. Concepts from graph signal processing are leveraged to learn the optimal mapping of multi-modal features, e.g. from images to disease classes. Related studies so far have considered image features that are extracted in a pre-processing step. We hypothesize that such an approach prevents the network from optimizing feature representations towards achieving the best performance in the graph network. We propose a new network architecture that exploits an inductive end-to-end learning approach for disease classification, where filters from both the CNN and the graph are trained jointly. We validate this architecture against state-of-the-art inductive graph networks and demonstrate significantly improved classification scores on a modified MNIST toy dataset, as well as comparable classification results with higher stability on a chest X-ray image dataset. Additionally, we explain how the structural information of the graph affects both the image filters and the feature learning.

InceptionGCN: Receptive Field Aware Graph Convolutional Network for Disease Prediction

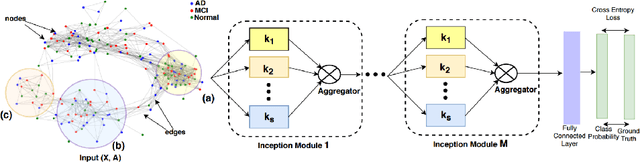
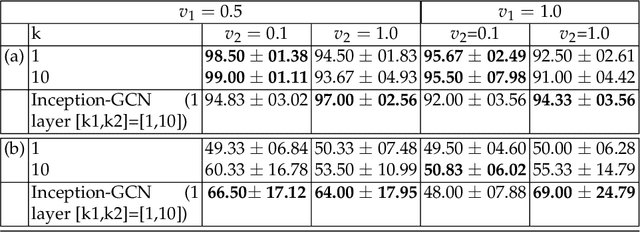
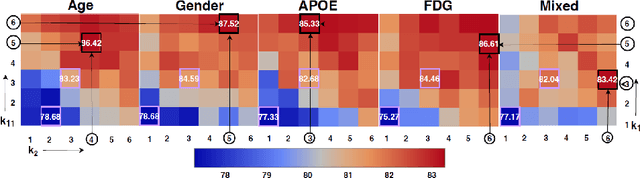
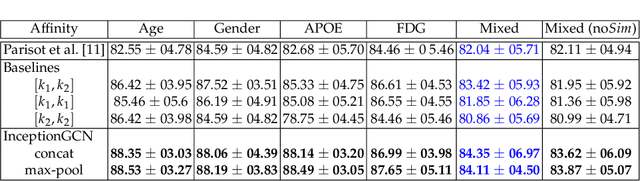
Geometric deep learning provides a principled and versatile manner for the integration of imaging and non-imaging modalities in the medical domain. Graph Convolutional Networks (GCNs) in particular have been explored on a wide variety of problems such as disease prediction, segmentation, and matrix completion by leveraging large, multimodal datasets. In this paper, we introduce a new spectral domain architecture for deep learning on graphs for disease prediction. The novelty lies in defining geometric 'inception modules' which are capable of capturing intra- and inter-graph structural heterogeneity during convolutions. We design filters with different kernel sizes to build our architecture. We show our disease prediction results on two publicly available datasets. Further, we provide insights on the behaviour of regular GCNs and our proposed model under varying input scenarios on simulated data.

Multi-modal Disease Classification in Incomplete Datasets Using Geometric Matrix Completion

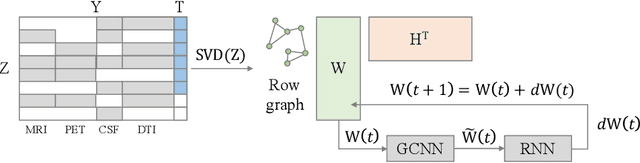
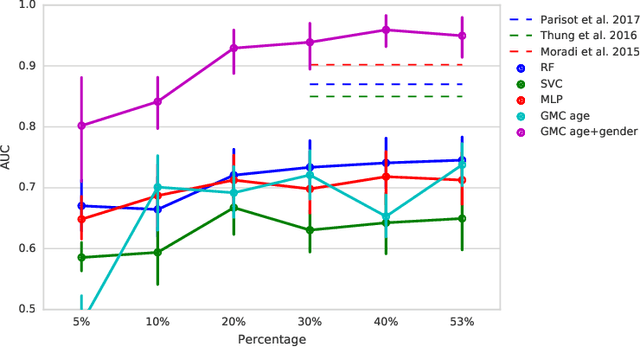
In large population-based studies and in clinical routine, tasks like disease diagnosis and progression prediction are inherently based on a rich set of multi-modal data, including imaging and other sensor data, clinical scores, phenotypes, labels and demographics. However, missing features, rater bias and inaccurate measurements are typical ailments of real-life medical datasets. Recently, it has been shown that deep learning with graph convolution neural networks (GCN) can outperform traditional machine learning in disease classification, but missing features remain an open problem. In this work, we follow up on the idea of modeling multi-modal disease classification as a matrix completion problem, with simultaneous classification and non-linear imputation of features. Compared to methods before, we arrange subjects in a graph-structure and solve classification through geometric matrix completion, which simulates a heat diffusion process that is learned and solved with a recurrent neural network. We demonstrate the potential of this method on the ADNI-based TADPOLE dataset and on the task of predicting the transition from MCI to Alzheimer's disease. With an AUC of 0.950 and classification accuracy of 87%, our approach outperforms standard linear and non-linear classifiers, as well as several state-of-the-art results in related literature, including a recently proposed GCN-based approach.