Georg Krempl
Performative Drift Resistant Classification Using Generative Domain Adversarial Networks
Apr 01, 2025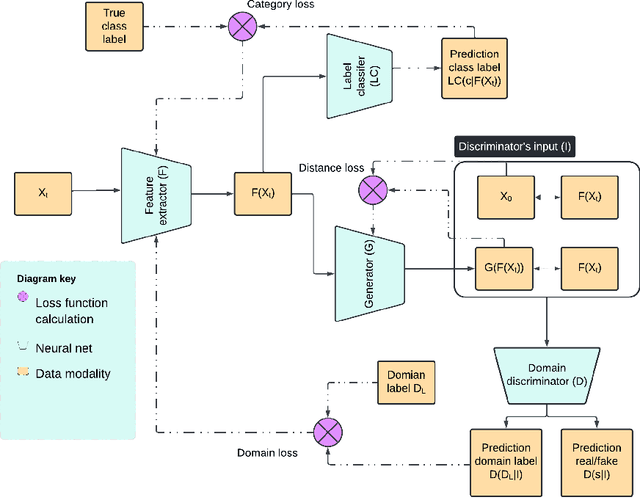
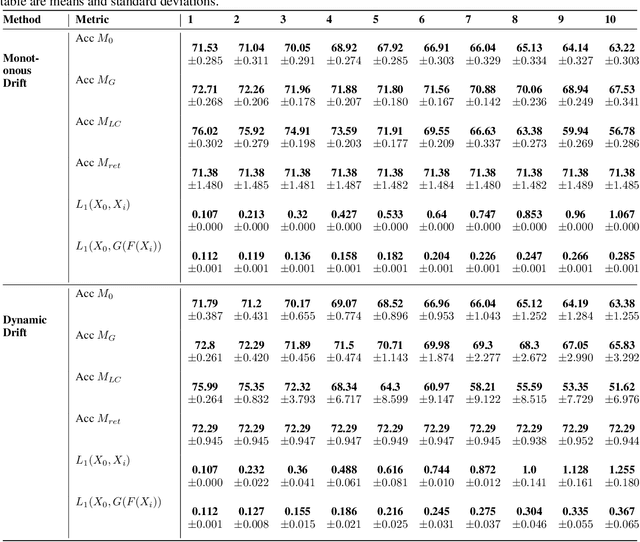
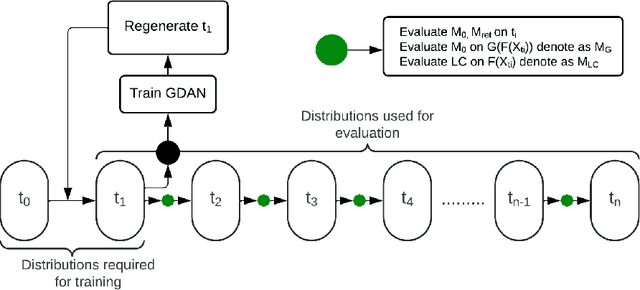
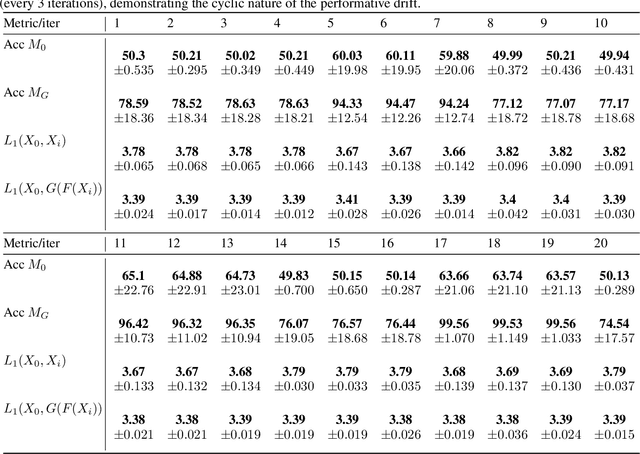
Abstract:Performative Drift is a special type of Concept Drift that occurs when a model's predictions influence the future instances the model will encounter. In these settings, retraining is not always feasible. In this work, we instead focus on drift understanding as a method for creating drift-resistant classifiers. To achieve this, we introduce the Generative Domain Adversarial Network (GDAN) which combines both Domain and Generative Adversarial Networks. Using GDAN, domain-invariant representations of incoming data are created and a generative network is used to reverse the effects of performative drift. Using semi-real and synthetic data generators, we empirically evaluate GDAN's ability to provide drift-resistant classification. Initial results are promising with GDAN limiting performance degradation over several timesteps. Additionally, GDAN's generative network can be used in tandem with other models to limit their performance degradation in the presence of performative drift. Lastly, we highlight the relationship between model retraining and the unpredictability of performative drift, providing deeper insights into the challenges faced when using traditional Concept Drift mitigation strategies in the performative setting.
Identifying Predictions That Influence the Future: Detecting Performative Concept Drift in Data Streams
Dec 13, 2024Abstract:Concept Drift has been extensively studied within the context of Stream Learning. However, it is often assumed that the deployed model's predictions play no role in the concept drift the system experiences. Closer inspection reveals that this is not always the case. Automated trading might be prone to self-fulfilling feedback loops. Likewise, malicious entities might adapt to evade detectors in the adversarial setting resulting in a self-negating feedback loop that requires the deployed models to constantly retrain. Such settings where a model may induce concept drift are called performative. In this work, we investigate this phenomenon. Our contributions are as follows: First, we define performative drift within a stream learning setting and distinguish it from other causes of drift. We introduce a novel type of drift detection task, aimed at identifying potential performative concept drift in data streams. We propose a first such performative drift detection approach, called CheckerBoard Performative Drift Detection (CB-PDD). We apply CB-PDD to both synthetic and semi-synthetic datasets that exhibit varying degrees of self-fulfilling feedback loops. Results are positive with CB-PDD showing high efficacy, low false detection rates, resilience to intrinsic drift, comparability to other drift detection techniques, and an ability to effectively detect performative drift in semi-synthetic datasets. Secondly, we highlight the role intrinsic (traditional) drift plays in obfuscating performative drift and discuss the implications of these findings as well as the limitations of CB-PDD.
Probabilistic Active Learning for Active Class Selection
Aug 09, 2021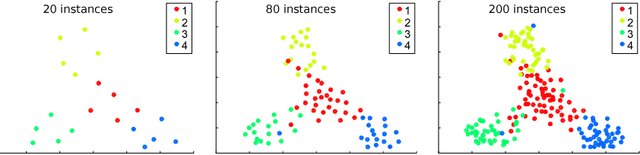
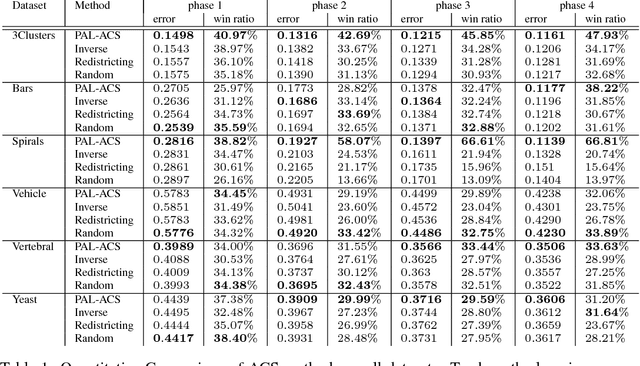
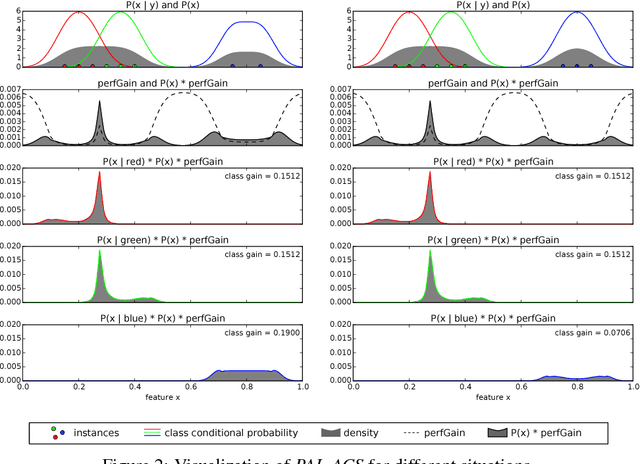
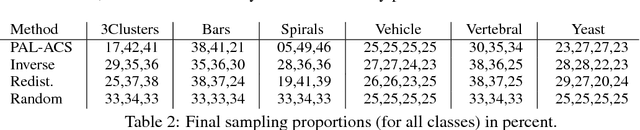
Abstract:In machine learning, active class selection (ACS) algorithms aim to actively select a class and ask the oracle to provide an instance for that class to optimize a classifier's performance while minimizing the number of requests. In this paper, we propose a new algorithm (PAL-ACS) that transforms the ACS problem into an active learning task by introducing pseudo instances. These are used to estimate the usefulness of an upcoming instance for each class using the performance gain model from probabilistic active learning. Our experimental evaluation (on synthetic and real data) shows the advantages of our algorithm compared to state-of-the-art algorithms. It effectively prefers the sampling of difficult classes and thereby improves the classification performance.
Active Selection of Classification Features
Feb 26, 2021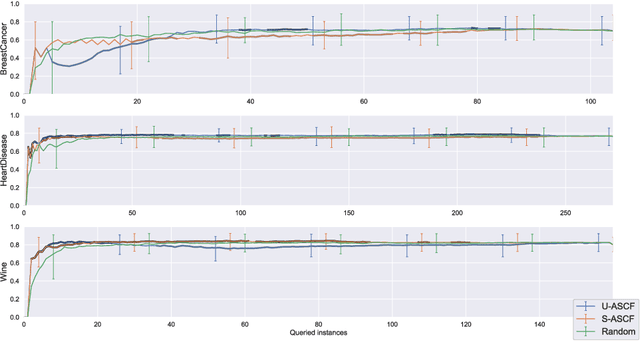
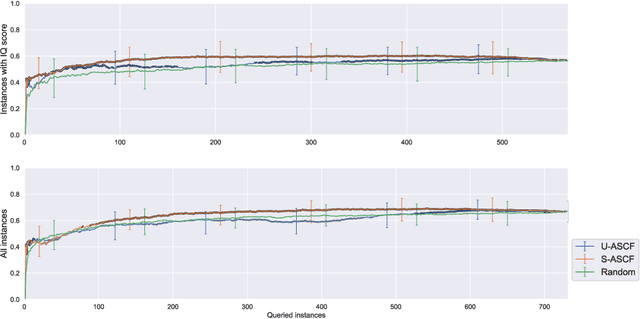
Abstract:Some data analysis applications comprise datasets, where explanatory variables are expensive or tedious to acquire, but auxiliary data are readily available and might help to construct an insightful training set. An example is neuroimaging research on mental disorders, specifically learning a diagnosis/prognosis model based on variables derived from expensive Magnetic Resonance Imaging (MRI) scans, which often requires large sample sizes. Auxiliary data, such as demographics, might help in selecting a smaller sample that comprises the individuals with the most informative MRI scans. In active learning literature, this problem has not yet been studied, despite promising results in related problem settings that concern the selection of instances or instance-feature pairs. Therefore, we formulate this complementary problem of Active Selection of Classification Features (ASCF): Given a primary task, which requires to learn a model f: x-> y to explain/predict the relationship between an expensive-to-acquire set of variables x and a class label y. Then, the ASCF-task is to use a set of readily available selection variables z to select these instances, that will improve the primary task's performance most when acquiring their expensive features z and including them to the primary training set. We propose two utility-based approaches for this problem, and evaluate their performance on three public real-world benchmark datasets. In addition, we illustrate the use of these approaches to efficiently acquire MRI scans in the context of neuroimaging research on mental disorders, based on a simulated study design with real MRI data.
Toward Optimal Probabilistic Active Learning Using a Bayesian Approach
Jun 02, 2020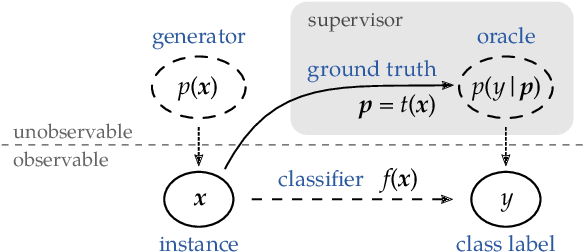
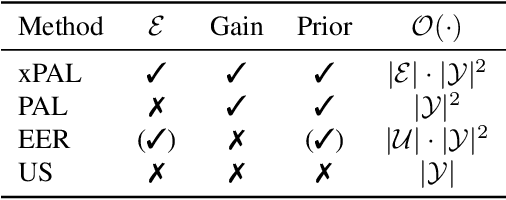
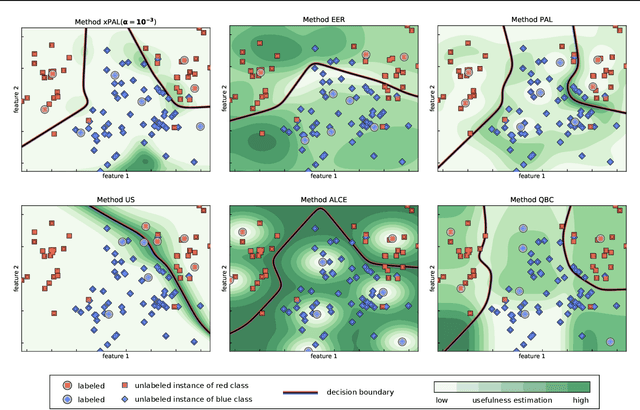
Abstract:Gathering labeled data to train well-performing machine learning models is one of the critical challenges in many applications. Active learning aims at reducing the labeling costs by an efficient and effective allocation of costly labeling resources. In this article, we propose a decision-theoretic selection strategy that (1) directly optimizes the gain in misclassification error, and (2) uses a Bayesian approach by introducing a conjugate prior distribution to determine the class posterior to deal with uncertainties. By reformulating existing selection strategies within our proposed model, we can explain which aspects are not covered in current state-of-the-art and why this leads to the superior performance of our approach. Extensive experiments on a large variety of datasets and different kernels validate our claims.
Temporal Density Extrapolation using a Dynamic Basis Approach
Jun 03, 2019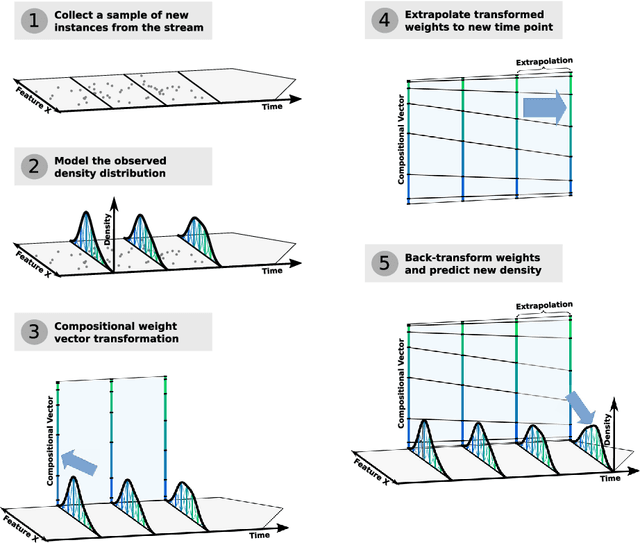

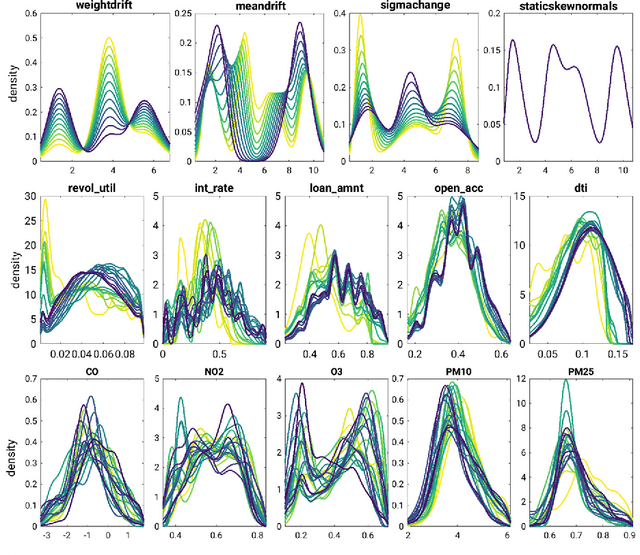
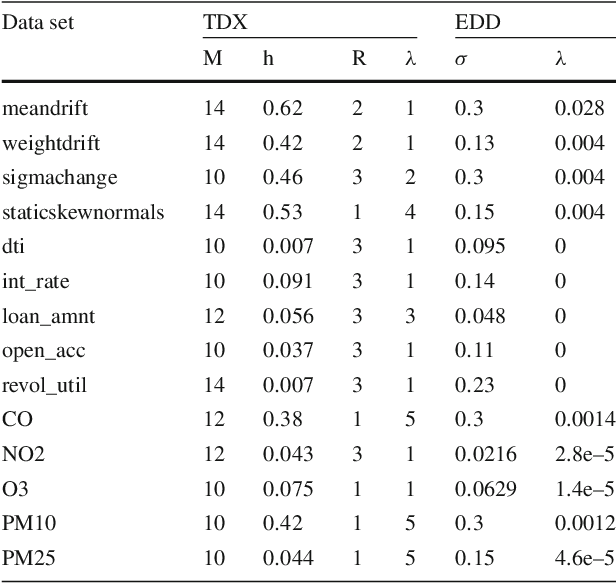
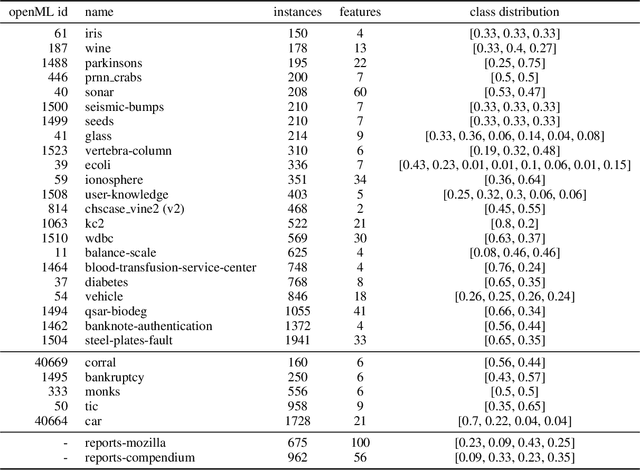
Abstract:Density estimation is a versatile technique underlying many data mining tasks and techniques,ranging from exploration and presentation of static data, to probabilistic classification, or identifying changes or irregularities in streaming data. With the pervasiveness of embedded systems and digitisation, this latter type of streaming and evolving data becomes more important. Nevertheless, research in density estimation has so far focused on stationary data, leaving the task of of extrapolating and predicting density at time points outside a training window an open problem. For this task, Temporal Density Extrapolation (TDX) is proposed. This novel method models and predicts gradual monotonous changes in a distribution. It is based on the expansion of basis functions, whose weights are modelled as functions of compositional data over time by using an isometric log-ratio transformation. Extrapolated density estimates are then obtained by extrapolating the weights to the requested time point, and querying the density from the basis functions with back-transformed weights. Our approach aims for broad applicability by neither being restricted to a specific parametric distribution, nor relying on cluster structure in the data.It requires only two additional extrapolation-specific parameters, for which reasonable defaults exist. Experimental evaluation on various data streams, synthetic as well as from the real-world domains of credit scoring and environmental health, shows that the model manages to capture monotonous drift patterns accurately and better than existing methods. Thereby, it requires not more than 1.5-times the run time of a corresponding static density estimation approach.
* Accepted for publication in Data Mining and Knowledge Discovery, Special issue of the ECML/PKDD 2019 Journal Track, Springer, 2019
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge