FairDeFace: Evaluating the Fairness and Adversarial Robustness of Face Obfuscation Methods

The lack of a common platform and benchmark datasets for evaluating face obfuscation methods has been a challenge, with every method being tested using arbitrary experiments, datasets, and metrics. While prior work has demonstrated that face recognition systems exhibit bias against some demographic groups, there exists a substantial gap in our understanding regarding the fairness of face obfuscation methods. Providing fair face obfuscation methods can ensure equitable protection across diverse demographic groups, especially since they can be used to preserve the privacy of vulnerable populations. To address these gaps, this paper introduces a comprehensive framework, named FairDeFace, designed to assess the adversarial robustness and fairness of face obfuscation methods. The framework introduces a set of modules encompassing data benchmarks, face detection and recognition algorithms, adversarial models, utility detection models, and fairness metrics. FairDeFace serves as a versatile platform where any face obfuscation method can be integrated, allowing for rigorous testing and comparison with other state-of-the-art methods. In its current implementation, FairDeFace incorporates 6 attacks, and several privacy, utility and fairness metrics. Using FairDeFace, and by conducting more than 500 experiments, we evaluated and compared the adversarial robustness of seven face obfuscation methods. This extensive analysis led to many interesting findings both in terms of the degree of robustness of existing methods and their biases against some gender or racial groups. FairDeFace also uses visualization of focused areas for both obfuscation and verification attacks to show not only which areas are mostly changed in the obfuscation process for some demographics, but also why they failed through focus area comparison of obfuscation and verification.

AXOLOTL: Fairness through Assisted Self-Debiasing of Large Language Model Outputs

Pre-trained Large Language Models (LLMs) have significantly advanced natural language processing capabilities but are susceptible to biases present in their training data, leading to unfair outcomes in various applications. While numerous strategies have been proposed to mitigate bias, they often require extensive computational resources and may compromise model performance. In this work, we introduce AXOLOTL, a novel post-processing framework, which operates agnostically across tasks and models, leveraging public APIs to interact with LLMs without direct access to internal parameters. Through a three-step process resembling zero-shot learning, AXOLOTL identifies biases, proposes resolutions, and guides the model to self-debias its outputs. This approach minimizes computational costs and preserves model performance, making AXOLOTL a promising tool for debiasing LLM outputs with broad applicability and ease of use.

Efficient Strongly Polynomial Algorithms for Quantile Regression

Linear Regression is a seminal technique in statistics and machine learning, where the objective is to build linear predictive models between a response (i.e., dependent) variable and one or more predictor (i.e., independent) variables. In this paper, we revisit the classical technique of Quantile Regression (QR), which is statistically a more robust alternative to the other classical technique of Ordinary Least Square Regression (OLS). However, while there exist efficient algorithms for OLS, almost all of the known results for QR are only weakly polynomial. Towards filling this gap, this paper proposes several efficient strongly polynomial algorithms for QR for various settings. For two dimensional QR, making a connection to the geometric concept of $k$-set, we propose an algorithm with a deterministic worst-case time complexity of $\mathcal{O}(n^{4/3} polylog(n))$ and an expected time complexity of $\mathcal{O}(n^{4/3})$ for the randomized version. We also propose a randomized divide-and-conquer algorithm -- RandomizedQR with an expected time complexity of $\mathcal{O}(n\log^2{(n)})$ for two dimensional QR problem. For the general case with more than two dimensions, our RandomizedQR algorithm has an expected time complexity of $\mathcal{O}(n^{d-1}\log^2{(n)})$.

Approximate Query Processing using Deep Generative Models

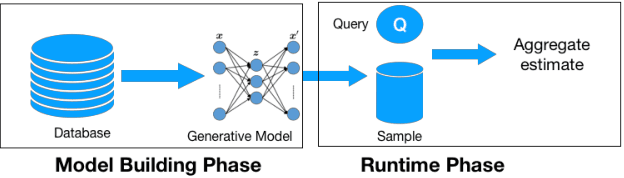
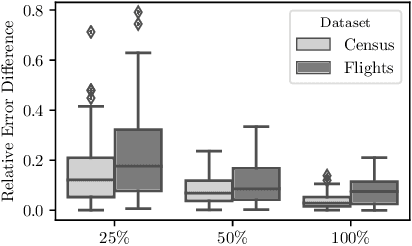
Data is generated at an unprecedented rate surpassing our ability to analyze them. One viable solution that was pioneered by the database community is Approximate Query Processing (AQP). AQP seeks to provide approximate answers to queries in a fraction of time needed for computing exact answers. This is often achieved by running the query on a pre-computed or on-demand derived sample and generating estimates for the entire dataset based on the result. In this work, we explore a novel approach for AQP utilizing deep learning (DL). We use deep generative models, an unsupervised learning based approach, to learn the data distribution faithfully in a compact manner (typically few hundred KBs). Queries could be answered approximately by generating samples from the learned model. This approach eliminates the dependency of AQP to a sample of fixed size and allows us to satisfy arbitrary accuracy requirements by generating as many samples as needed very fast. While we specifically focus on variational autoencoders (VAE), we demonstrate how our approach could also be used for other popular DL models such as generative adversarial networks (GAN) and deep Bayesian networks (DBN). Our other contributions include (a) identifying model bias and minimizing it through a rejection sampling based approach (b) An algorithm to build model ensembles for AQP for improved accuracy and (c) an analysis of VAE latent space to understand its suitability to AQP. Our extensive experiments show that deep learning is a very promising approach for AQP.

Multi-Attribute Selectivity Estimation Using Deep Learning

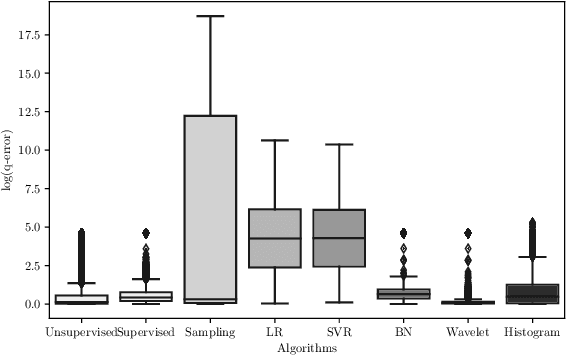
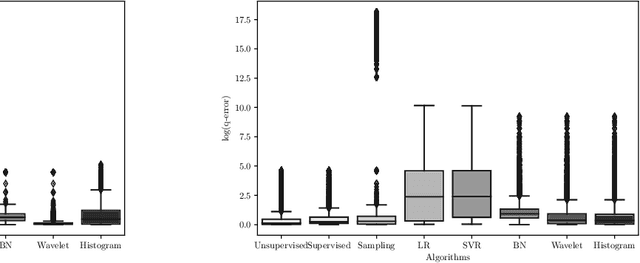
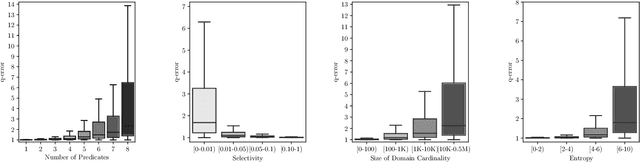
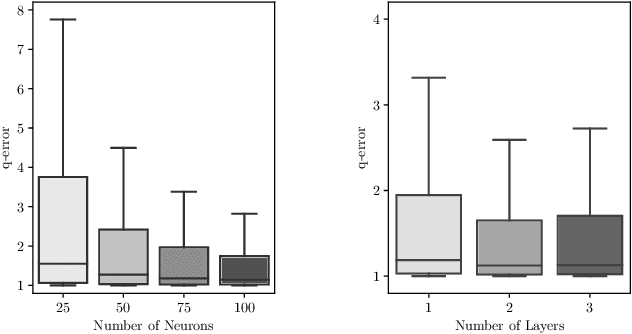
Selectivity estimation - the problem of estimating the result size of queries - is a fundamental yet challenging problem in databases. Accurate estimation of query selectivity involving multiple correlated attributes is especially challenging. Poor cardinality estimates could result in the selection of bad plans by the query optimizer. In this paper, we investigate the feasibility of using deep learning based approaches for challenging scenarios such as queries involving multiple predicates and/or low selectivity. Specifically, we propose two complementary approaches. Our first approach considers selectivity as an unsupervised deep density estimation problem. We successfully introduce techniques from neural density estimation for this purpose. The key idea is to decompose the joint distribution into a set of tractable conditional probability distributions such that they satisfy the autoregressive property. Our second approach formulates selectivity estimation as a supervised deep learning problem that predicts the selectivity of a given query. We also introduce and address a number of practical challenges arising when adapting deep learning for relational data. These include query/data featurization, incorporating query workload information in a deep learning framework and the dynamic scenario where both data and workload queries could be updated. Our extensive experiments with a special emphasis on queries with a large number of predicates and/or small result sizes demonstrates that deep learning based techniques are a promising research avenue for selectivity estimation worthy of further investigation.