WANCO: Weak Adversarial Networks for Constrained Optimization problems

This paper focuses on integrating the networks and adversarial training into constrained optimization problems to develop a framework algorithm for constrained optimization problems. For such problems, we first transform them into minimax problems using the augmented Lagrangian method and then use two (or several) deep neural networks(DNNs) to represent the primal and dual variables respectively. The parameters in the neural networks are then trained by an adversarial process. The proposed architecture is relatively insensitive to the scale of values of different constraints when compared to penalty based deep learning methods. Through this type of training, the constraints are imposed better based on the augmented Lagrangian multipliers. Extensive examples for optimization problems with scalar constraints, nonlinear constraints, partial differential equation constraints, and inequality constraints are considered to show the capability and robustness of the proposed method, with applications ranging from Ginzburg--Landau energy minimization problems, partition problems, fluid-solid topology optimization, to obstacle problems.

VBIM-Net: Variational Born Iterative Network for Inverse Scattering Problems

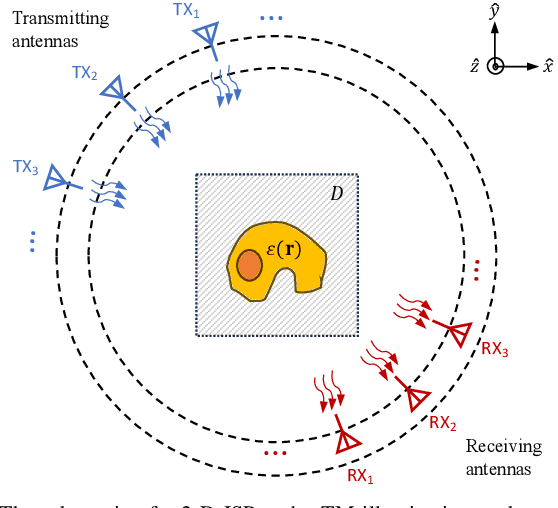
Recently, studies have shown the potential of integrating field-type iterative methods with deep learning (DL) techniques in solving inverse scattering problems (ISPs). In this article, we propose a novel Variational Born Iterative Network, namely, VBIM-Net, to solve the full-wave ISPs with significantly improved flexibility and inversion quality. The proposed VBIM-Net emulates the alternating updates of the total electric field and the contrast in the variational Born iterative method (VBIM) by multiple layers of subnetworks. We embed the calculation of the contrast variation into each of the subnetworks, converting the scattered field residual into an approximate contrast variation and then enhancing it by a U-Net, thus avoiding the requirement of matched measurement dimension and grid resolution as in existing approaches. The total field and contrast of each layer's output is supervised in the loss function of VBIM-Net, which guarantees the physical interpretability of variables of the subnetworks. In addition, we design a training scheme with extra noise to enhance the model's stability. Extensive numerical results on synthetic and experimental data both verify the inversion quality, generalization ability, and robustness of the proposed VBIM-Net. This work may provide some new inspiration for the design of efficient field-type DL schemes.

ParticleWNN: a Novel Neural Networks Framework for Solving Partial Differential Equations

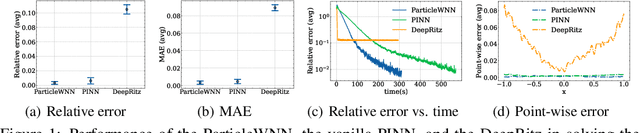
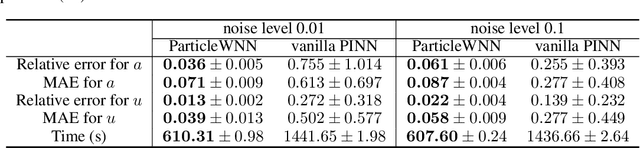
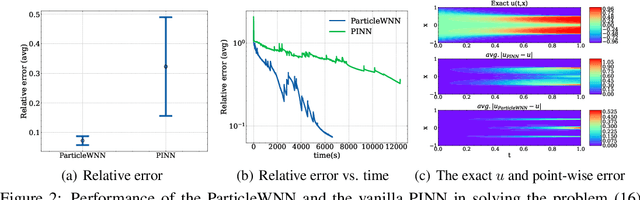
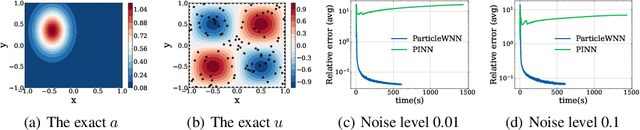
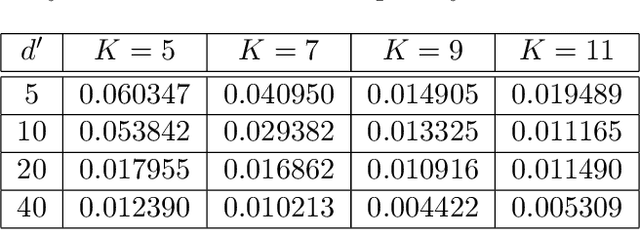
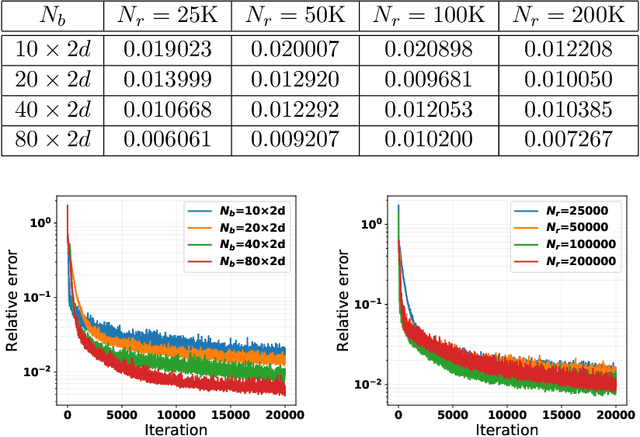
Deep neural networks (DNNs) have been widely used to solve partial differential equations (PDEs) in recent years. In this work, a novel deep learning-based framework named Particle Weak-form based Neural Networks (ParticleWNN) is developed for solving PDEs in the weak form. In this framework, the trial space is chosen as the space of DNNs, and the test space is constructed by functions compactly supported in extremely small regions whose centers are particles. To train the neural networks, an R-adaptive strategy is designed to adaptively modify the radius of regions during training. The ParticleWNN inherits the advantages of weak/variational formulation, such as requiring less regularity of the solution and a small number of quadrature points for computing the integrals. Moreover, due to the special construction of the test functions, the ParticleWNN allows local training of networks, parallel implementation, and integral calculations only in extremely small regions. The framework is particularly desirable for solving problems with high-dimensional and complex domains. The efficiency and accuracy of the ParticleWNN are demonstrated with several numerical examples. The numerical results show clear advantages of the ParticleWNN over the state-of-the-art methods.

Numerical Solution of Inverse Problems by Weak Adversarial Networks

We consider a weak adversarial network approach to numerically solve a class of inverse problems, including electrical impedance tomography and dynamic electrical impedance tomography problems. We leverage the weak formulation of PDE in the given inverse problem, and parameterize the solution and the test function as deep neural networks. The weak formulation and the boundary conditions induce a minimax problem of a saddle function of the network parameters. As the parameters are alternatively updated, the network gradually approximates the solution of the inverse problem. We provide theoretical justifications on the convergence of the proposed algorithm. Our method is completely mesh-free without any spatial discretization, and is particularly suitable for problems with high dimensionality and low regularity on solutions. Numerical experiments on a variety of test inverse problems demonstrate the promising accuracy and efficiency of our approach.