Weak neural variational inference for solving Bayesian inverse problems without forward models: applications in elastography

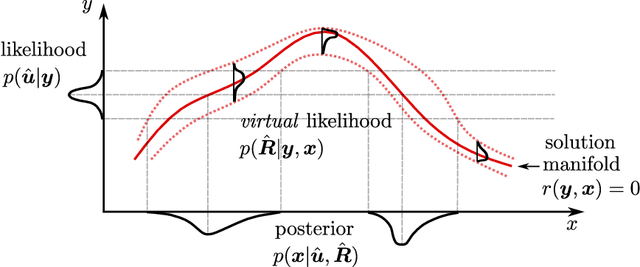
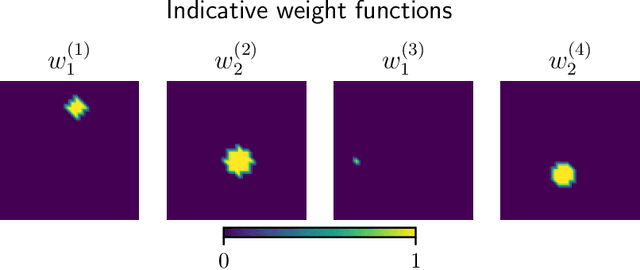
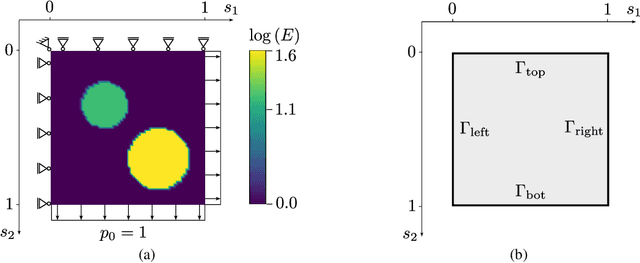
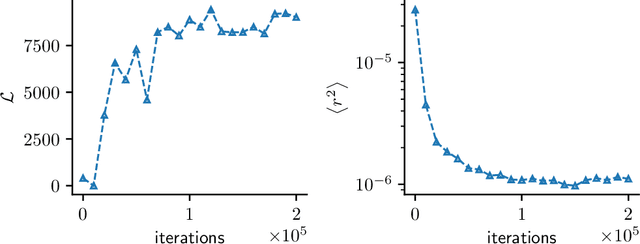
In this paper, we introduce a novel, data-driven approach for solving high-dimensional Bayesian inverse problems based on partial differential equations (PDEs), called Weak Neural Variational Inference (WNVI). The method complements real measurements with virtual observations derived from the physical model. In particular, weighted residuals are employed as probes to the governing PDE in order to formulate and solve a Bayesian inverse problem without ever formulating nor solving a forward model. The formulation treats the state variables of the physical model as latent variables, inferred using Stochastic Variational Inference (SVI), along with the usual unknowns. The approximate posterior employed uses neural networks to approximate the inverse mapping from state variables to the unknowns. We illustrate the proposed method in a biomedical setting where we infer spatially varying material properties from noisy tissue deformation data. We demonstrate that WNVI is not only as accurate and more efficient than traditional methods that rely on repeatedly solving the (non)linear forward problem as a black-box, but it can also handle ill-posed forward problems (e.g., with insufficient boundary conditions).

ParticleWNN: a Novel Neural Networks Framework for Solving Partial Differential Equations

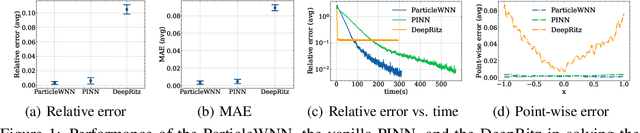
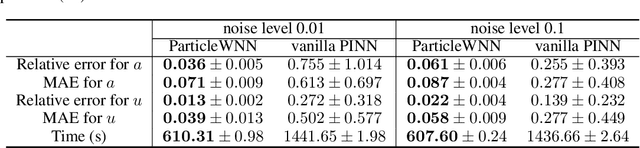
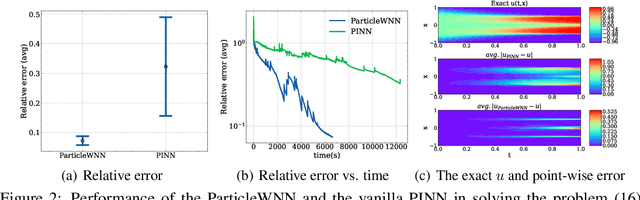
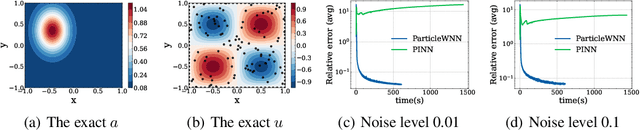
Deep neural networks (DNNs) have been widely used to solve partial differential equations (PDEs) in recent years. In this work, a novel deep learning-based framework named Particle Weak-form based Neural Networks (ParticleWNN) is developed for solving PDEs in the weak form. In this framework, the trial space is chosen as the space of DNNs, and the test space is constructed by functions compactly supported in extremely small regions whose centers are particles. To train the neural networks, an R-adaptive strategy is designed to adaptively modify the radius of regions during training. The ParticleWNN inherits the advantages of weak/variational formulation, such as requiring less regularity of the solution and a small number of quadrature points for computing the integrals. Moreover, due to the special construction of the test functions, the ParticleWNN allows local training of networks, parallel implementation, and integral calculations only in extremely small regions. The framework is particularly desirable for solving problems with high-dimensional and complex domains. The efficiency and accuracy of the ParticleWNN are demonstrated with several numerical examples. The numerical results show clear advantages of the ParticleWNN over the state-of-the-art methods.

Numerical Solution of Inverse Problems by Weak Adversarial Networks

We consider a weak adversarial network approach to numerically solve a class of inverse problems, including electrical impedance tomography and dynamic electrical impedance tomography problems. We leverage the weak formulation of PDE in the given inverse problem, and parameterize the solution and the test function as deep neural networks. The weak formulation and the boundary conditions induce a minimax problem of a saddle function of the network parameters. As the parameters are alternatively updated, the network gradually approximates the solution of the inverse problem. We provide theoretical justifications on the convergence of the proposed algorithm. Our method is completely mesh-free without any spatial discretization, and is particularly suitable for problems with high dimensionality and low regularity on solutions. Numerical experiments on a variety of test inverse problems demonstrate the promising accuracy and efficiency of our approach.