Quantification of model error for inverse problems in the Weak Neural Variational Inference framework

We present a novel extension of the Weak Neural Variational Inference (WNVI) framework for probabilistic material property estimation that explicitly quantifies model errors in PDE-based inverse problems. Traditional approaches assume the correctness of all governing equations, including potentially unreliable constitutive laws, which can lead to biased estimates and misinterpretations. Our proposed framework addresses this limitation by distinguishing between reliable governing equations, such as conservation laws, and uncertain constitutive relationships. By treating all state variables as latent random variables, we enforce these equations through separate sets of residuals, leveraging a virtual likelihood approach with weighted residuals. This formulation not only identifies regions where constitutive laws break down but also improves robustness against model uncertainties without relying on a fully trustworthy forward model. We demonstrate the effectiveness of our approach in the context of elastography, showing that it provides a structured, interpretable, and computationally efficient alternative to traditional model error correction techniques. Our findings suggest that the proposed framework enhances the accuracy and reliability of material property estimation by offering a principled way to incorporate uncertainty in constitutive modeling.

Weak neural variational inference for solving Bayesian inverse problems without forward models: applications in elastography

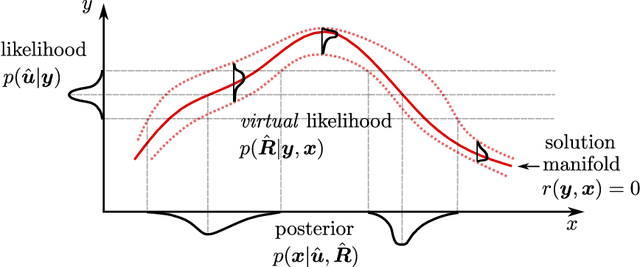
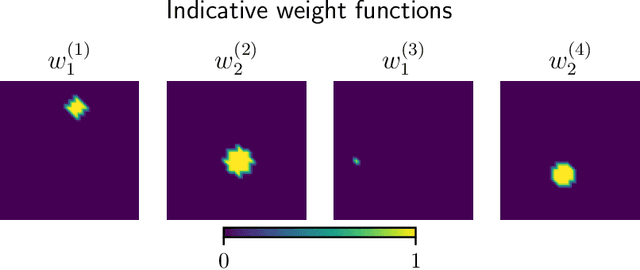
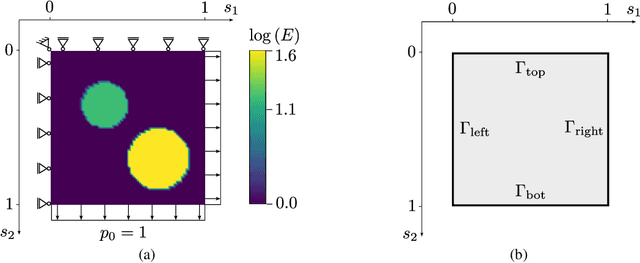
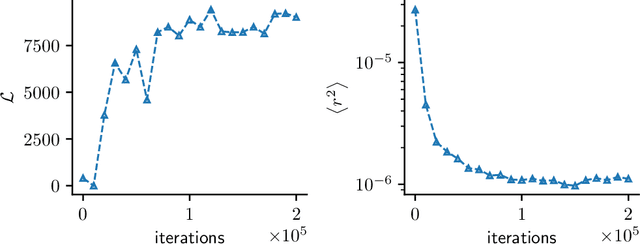
In this paper, we introduce a novel, data-driven approach for solving high-dimensional Bayesian inverse problems based on partial differential equations (PDEs), called Weak Neural Variational Inference (WNVI). The method complements real measurements with virtual observations derived from the physical model. In particular, weighted residuals are employed as probes to the governing PDE in order to formulate and solve a Bayesian inverse problem without ever formulating nor solving a forward model. The formulation treats the state variables of the physical model as latent variables, inferred using Stochastic Variational Inference (SVI), along with the usual unknowns. The approximate posterior employed uses neural networks to approximate the inverse mapping from state variables to the unknowns. We illustrate the proposed method in a biomedical setting where we infer spatially varying material properties from noisy tissue deformation data. We demonstrate that WNVI is not only as accurate and more efficient than traditional methods that rely on repeatedly solving the (non)linear forward problem as a black-box, but it can also handle ill-posed forward problems (e.g., with insufficient boundary conditions).