Energy-Based Coarse-Graining in Molecular Dynamics: A Flow-Based Framework Without Data

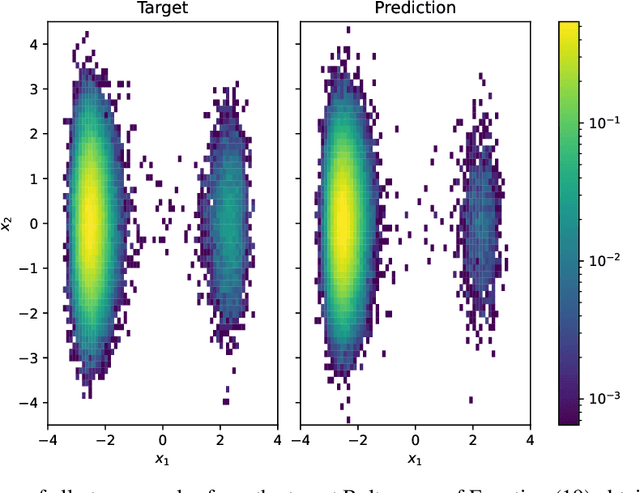
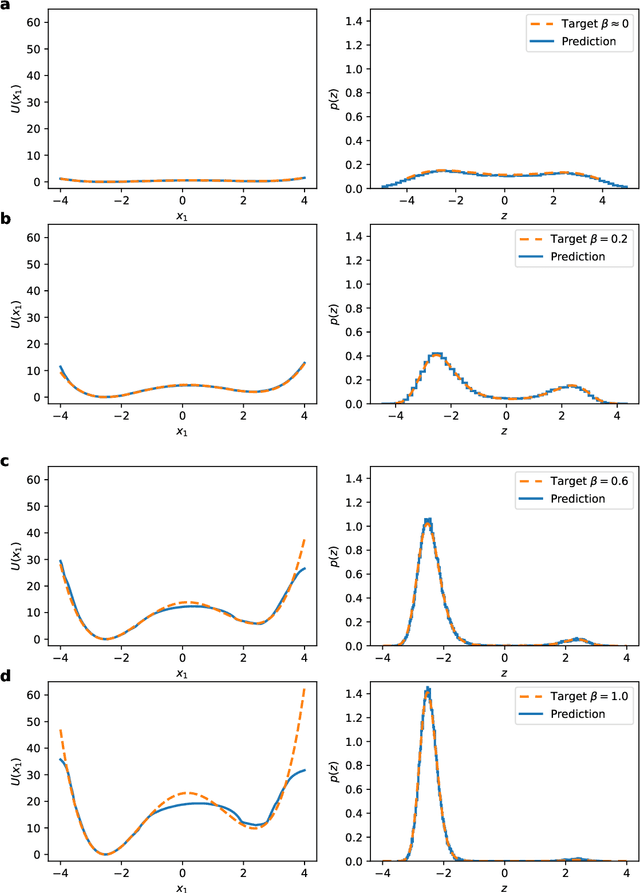
Coarse-grained (CG) models offer an effective route to reducing the complexity of molecular simulations, yet conventional approaches depend heavily on long all-atom molecular dynamics (MD) trajectories to adequately sample configurational space. This data-driven dependence limits their accuracy and generalizability, as unvisited configurations remain excluded from the resulting CG model. We introduce a data-free generative framework for coarse-graining that directly targets the all-atom Boltzmann distribution. Our model defines a structured latent space comprising slow collective variables, which are statistically associated with multimodal marginal densities capturing metastable states, and fast variables, which represent the remaining degrees of freedom with simple, unimodal conditional distributions. A potentially learnable, bijective map from the full latent space to the all-atom configuration space enables automatic and accurate reconstruction of molecular structures. The model is trained using an energy-based objective that minimizes the reverse Kullback-Leibler divergence, relying solely on the interatomic potential rather than sampled trajectories. A tempering scheme is used to stabilize training and promote exploration of diverse configurations. Once trained, the model can generate unbiased, one-shot equilibrium all-atom samples. We validate the method on two synthetic systems-a double-well potential and a Gaussian mixture-as well as on the benchmark alanine dipeptide. The model captures all relevant modes of the Boltzmann distribution, accurately reconstructs atomic configurations, and learns physically meaningful coarse-grained representations, all without any simulation data.

Quantification of model error for inverse problems in the Weak Neural Variational Inference framework

We present a novel extension of the Weak Neural Variational Inference (WNVI) framework for probabilistic material property estimation that explicitly quantifies model errors in PDE-based inverse problems. Traditional approaches assume the correctness of all governing equations, including potentially unreliable constitutive laws, which can lead to biased estimates and misinterpretations. Our proposed framework addresses this limitation by distinguishing between reliable governing equations, such as conservation laws, and uncertain constitutive relationships. By treating all state variables as latent random variables, we enforce these equations through separate sets of residuals, leveraging a virtual likelihood approach with weighted residuals. This formulation not only identifies regions where constitutive laws break down but also improves robustness against model uncertainties without relying on a fully trustworthy forward model. We demonstrate the effectiveness of our approach in the context of elastography, showing that it provides a structured, interpretable, and computationally efficient alternative to traditional model error correction techniques. Our findings suggest that the proposed framework enhances the accuracy and reliability of material property estimation by offering a principled way to incorporate uncertainty in constitutive modeling.

Physics-constrained, data-driven discovery of coarse-grained dynamics

The combination of high-dimensionality and disparity of time scales encountered in many problems in computational physics has motivated the development of coarse-grained (CG) models. In this paper, we advocate the paradigm of data-driven discovery for extract- ing governing equations by employing fine-scale simulation data. In particular, we cast the coarse-graining process under a probabilistic state-space model where the transition law dic- tates the evolution of the CG state variables and the emission law the coarse-to-fine map. The directed probabilistic graphical model implied, suggests that given values for the fine- grained (FG) variables, probabilistic inference tools must be employed to identify the cor- responding values for the CG states and to that end, we employ Stochastic Variational In- ference. We advocate a sparse Bayesian learning perspective which avoids overfitting and reveals the most salient features in the CG evolution law. The formulation adopted enables the quantification of a crucial, and often neglected, component in the CG process, i.e. the pre- dictive uncertainty due to information loss. Furthermore, it is capable of reconstructing the evolution of the full, fine-scale system. We demonstrate the efficacy of the proposed frame- work in high-dimensional systems of random walkers.

Multimodal, high-dimensional, model-based, Bayesian inverse problems with applications in biomechanics

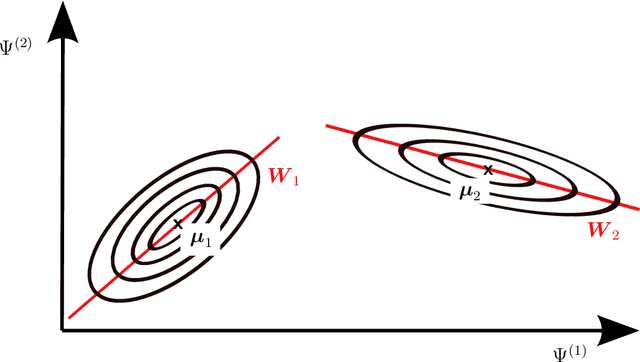
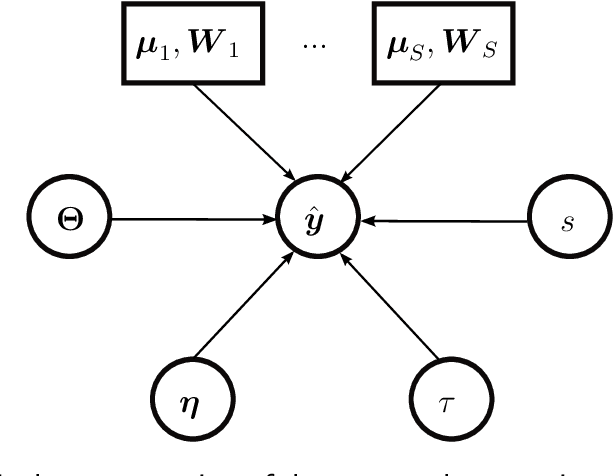
This paper is concerned with the numerical solution of model-based, Bayesian inverse problems. We are particularly interested in cases where the cost of each likelihood evaluation (forward-model call) is expensive and the number of un- known (latent) variables is high. This is the setting in many problems in com- putational physics where forward models with nonlinear PDEs are used and the parameters to be calibrated involve spatio-temporarily varying coefficients, which upon discretization give rise to a high-dimensional vector of unknowns. One of the consequences of the well-documented ill-posedness of inverse prob- lems is the possibility of multiple solutions. While such information is contained in the posterior density in Bayesian formulations, the discovery of a single mode, let alone multiple, is a formidable task. The goal of the present paper is two- fold. On one hand, we propose approximate, adaptive inference strategies using mixture densities to capture multi-modal posteriors, and on the other, to ex- tend our work in [1] with regards to effective dimensionality reduction techniques that reveal low-dimensional subspaces where the posterior variance is mostly concentrated. We validate the model proposed by employing Importance Sam- pling which confirms that the bias introduced is small and can be efficiently corrected if the analyst wishes to do so. We demonstrate the performance of the proposed strategy in nonlinear elastography where the identification of the mechanical properties of biological materials can inform non-invasive, medical di- agnosis. The discovery of multiple modes (solutions) in such problems is critical in achieving the diagnostic objectives.

Sparse Variational Bayesian Approximations for Nonlinear Inverse Problems: applications in nonlinear elastography

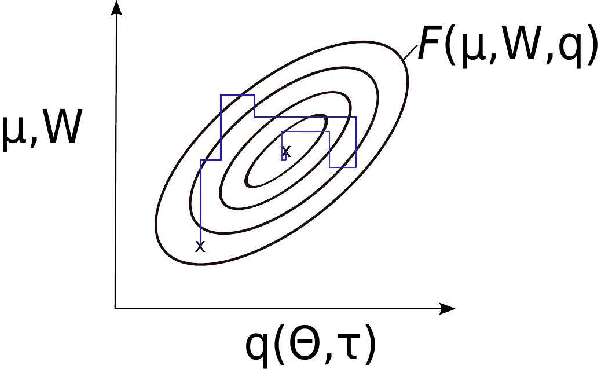
This paper presents an efficient Bayesian framework for solving nonlinear, high-dimensional model calibration problems. It is based on a Variational Bayesian formulation that aims at approximating the exact posterior by means of solving an optimization problem over an appropriately selected family of distributions. The goal is two-fold. Firstly, to find lower-dimensional representations of the unknown parameter vector that capture as much as possible of the associated posterior density, and secondly to enable the computation of the approximate posterior density with as few forward calls as possible. We discuss how these objectives can be achieved by using a fully Bayesian argumentation and employing the marginal likelihood or evidence as the ultimate model validation metric for any proposed dimensionality reduction. We demonstrate the performance of the proposed methodology for problems in nonlinear elastography where the identification of the mechanical properties of biological materials can inform non-invasive, medical diagnosis. An Importance Sampling scheme is finally employed in order to validate the results and assess the efficacy of the approximations provided.

Scalable Bayesian reduced-order models for high-dimensional multiscale dynamical systems

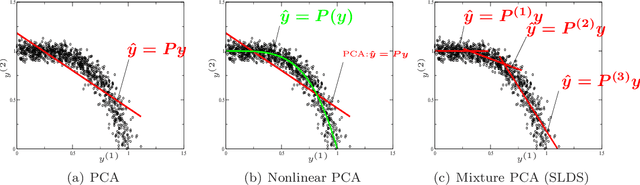
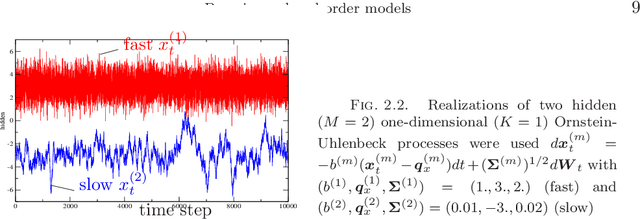
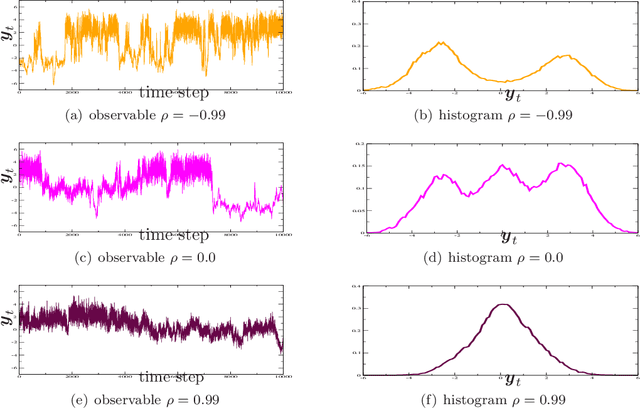
While existing mathematical descriptions can accurately account for phenomena at microscopic scales (e.g. molecular dynamics), these are often high-dimensional, stochastic and their applicability over macroscopic time scales of physical interest is computationally infeasible or impractical. In complex systems, with limited physical insight on the coherent behavior of their constituents, the only available information is data obtained from simulations of the trajectories of huge numbers of degrees of freedom over microscopic time scales. This paper discusses a Bayesian approach to deriving probabilistic coarse-grained models that simultaneously address the problems of identifying appropriate reduced coordinates and the effective dynamics in this lower-dimensional representation. At the core of the models proposed lie simple, low-dimensional dynamical systems which serve as the building blocks of the global model. These approximate the latent, generating sources and parameterize the reduced-order dynamics. We discuss parallelizable, online inference and learning algorithms that employ Sequential Monte Carlo samplers and scale linearly with the dimensionality of the observed dynamics. We propose a Bayesian adaptive time-integration scheme that utilizes probabilistic predictive estimates and enables rigorous concurrent s imulation over macroscopic time scales. The data-driven perspective advocated assimilates computational and experimental data and thus can materialize data-model fusion. It can deal with applications that lack a mathematical description and where only observational data is available. Furthermore, it makes non-intrusive use of existing computational models.