Multimodal, high-dimensional, model-based, Bayesian inverse problems with applications in biomechanics

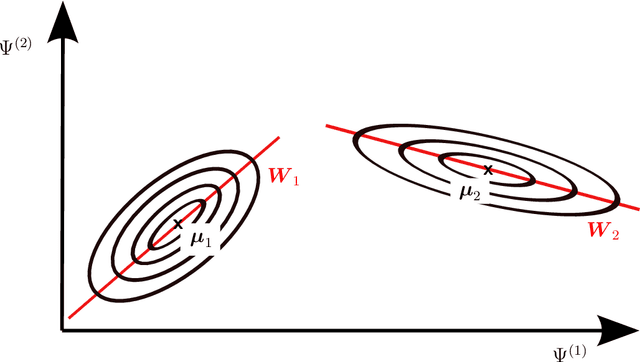
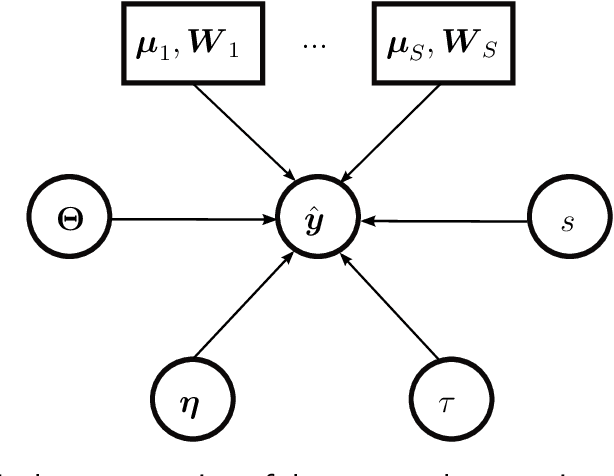
This paper is concerned with the numerical solution of model-based, Bayesian inverse problems. We are particularly interested in cases where the cost of each likelihood evaluation (forward-model call) is expensive and the number of un- known (latent) variables is high. This is the setting in many problems in com- putational physics where forward models with nonlinear PDEs are used and the parameters to be calibrated involve spatio-temporarily varying coefficients, which upon discretization give rise to a high-dimensional vector of unknowns. One of the consequences of the well-documented ill-posedness of inverse prob- lems is the possibility of multiple solutions. While such information is contained in the posterior density in Bayesian formulations, the discovery of a single mode, let alone multiple, is a formidable task. The goal of the present paper is two- fold. On one hand, we propose approximate, adaptive inference strategies using mixture densities to capture multi-modal posteriors, and on the other, to ex- tend our work in [1] with regards to effective dimensionality reduction techniques that reveal low-dimensional subspaces where the posterior variance is mostly concentrated. We validate the model proposed by employing Importance Sam- pling which confirms that the bias introduced is small and can be efficiently corrected if the analyst wishes to do so. We demonstrate the performance of the proposed strategy in nonlinear elastography where the identification of the mechanical properties of biological materials can inform non-invasive, medical di- agnosis. The discovery of multiple modes (solutions) in such problems is critical in achieving the diagnostic objectives.

Sparse Variational Bayesian Approximations for Nonlinear Inverse Problems: applications in nonlinear elastography

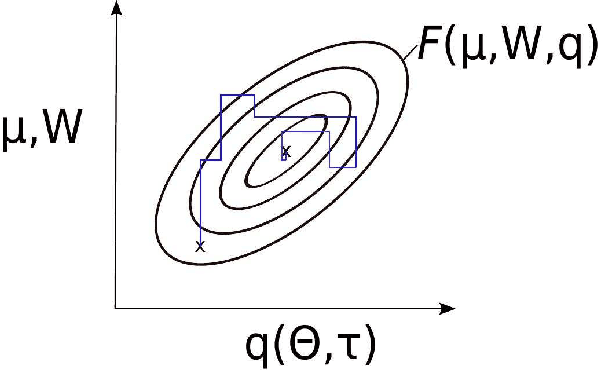
This paper presents an efficient Bayesian framework for solving nonlinear, high-dimensional model calibration problems. It is based on a Variational Bayesian formulation that aims at approximating the exact posterior by means of solving an optimization problem over an appropriately selected family of distributions. The goal is two-fold. Firstly, to find lower-dimensional representations of the unknown parameter vector that capture as much as possible of the associated posterior density, and secondly to enable the computation of the approximate posterior density with as few forward calls as possible. We discuss how these objectives can be achieved by using a fully Bayesian argumentation and employing the marginal likelihood or evidence as the ultimate model validation metric for any proposed dimensionality reduction. We demonstrate the performance of the proposed methodology for problems in nonlinear elastography where the identification of the mechanical properties of biological materials can inform non-invasive, medical diagnosis. An Importance Sampling scheme is finally employed in order to validate the results and assess the efficacy of the approximations provided.