Weak neural variational inference for solving Bayesian inverse problems without forward models: applications in elastography
Paper and Code
Jul 30, 2024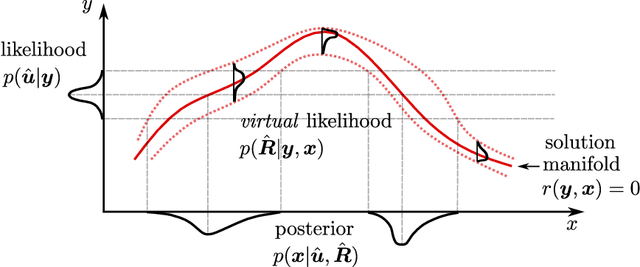
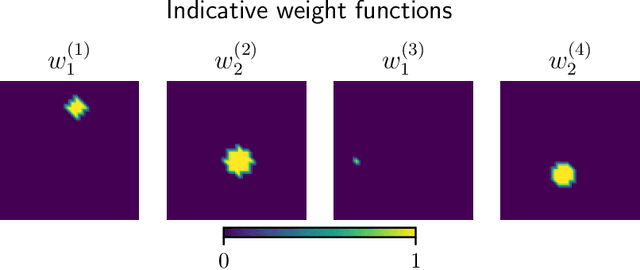
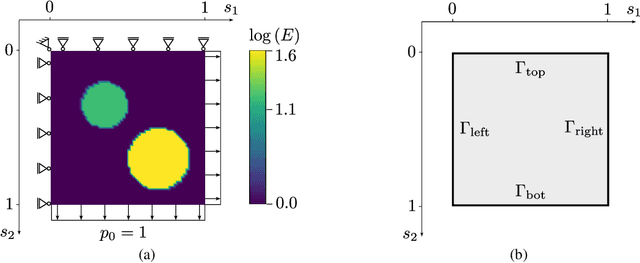
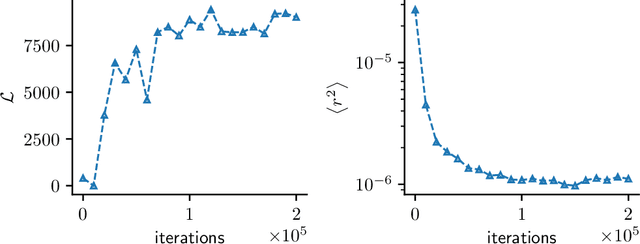
In this paper, we introduce a novel, data-driven approach for solving high-dimensional Bayesian inverse problems based on partial differential equations (PDEs), called Weak Neural Variational Inference (WNVI). The method complements real measurements with virtual observations derived from the physical model. In particular, weighted residuals are employed as probes to the governing PDE in order to formulate and solve a Bayesian inverse problem without ever formulating nor solving a forward model. The formulation treats the state variables of the physical model as latent variables, inferred using Stochastic Variational Inference (SVI), along with the usual unknowns. The approximate posterior employed uses neural networks to approximate the inverse mapping from state variables to the unknowns. We illustrate the proposed method in a biomedical setting where we infer spatially varying material properties from noisy tissue deformation data. We demonstrate that WNVI is not only as accurate and more efficient than traditional methods that rely on repeatedly solving the (non)linear forward problem as a black-box, but it can also handle ill-posed forward problems (e.g., with insufficient boundary conditions).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge