Quantum Maximum Entropy Inference and Hamiltonian Learning

Maximum entropy inference and learning of graphical models are pivotal tasks in learning theory and optimization. This work extends algorithms for these problems, including generalized iterative scaling (GIS) and gradient descent (GD), to the quantum realm. While the generalization, known as quantum iterative scaling (QIS), is straightforward, the key challenge lies in the non-commutative nature of quantum problem instances, rendering the convergence rate analysis significantly more challenging than the classical case. Our principal technical contribution centers on a rigorous analysis of the convergence rates, involving the establishment of both lower and upper bounds on the spectral radius of the Jacobian matrix for each iteration of these algorithms. Furthermore, we explore quasi-Newton methods to enhance the performance of QIS and GD. Specifically, we propose using Anderson mixing and the L-BFGS method for QIS and GD, respectively. These quasi-Newton techniques exhibit remarkable efficiency gains, resulting in orders of magnitude improvements in performance. As an application, our algorithms provide a viable approach to designing Hamiltonian learning algorithms.

Delta Tuning: A Comprehensive Study of Parameter Efficient Methods for Pre-trained Language Models

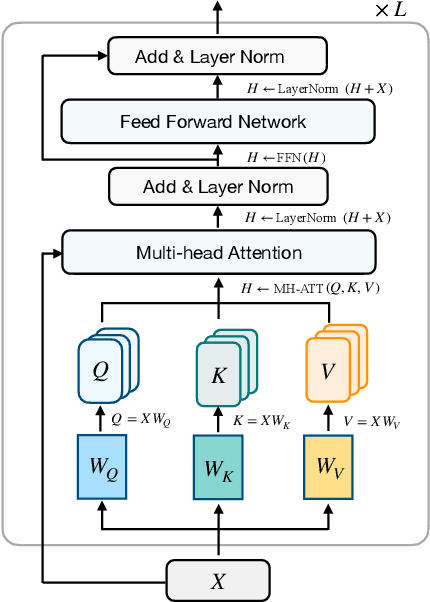
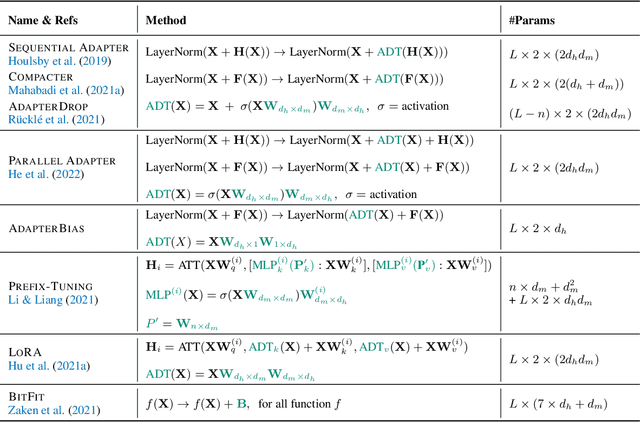
Despite the success, the process of fine-tuning large-scale PLMs brings prohibitive adaptation costs. In fact, fine-tuning all the parameters of a colossal model and retaining separate instances for different tasks are practically infeasible. This necessitates a new branch of research focusing on the parameter-efficient adaptation of PLMs, dubbed as delta tuning in this paper. In contrast with the standard fine-tuning, delta tuning only fine-tunes a small portion of the model parameters while keeping the rest untouched, largely reducing both the computation and storage costs. Recent studies have demonstrated that a series of delta tuning methods with distinct tuned parameter selection could achieve performance on a par with full-parameter fine-tuning, suggesting a new promising way of stimulating large-scale PLMs. In this paper, we first formally describe the problem of delta tuning and then comprehensively review recent delta tuning approaches. We also propose a unified categorization criterion that divide existing delta tuning methods into three groups: addition-based, specification-based, and reparameterization-based methods. Though initially proposed as an efficient method to steer large models, we believe that some of the fascinating evidence discovered along with delta tuning could help further reveal the mechanisms of PLMs and even deep neural networks. To this end, we discuss the theoretical principles underlying the effectiveness of delta tuning and propose frameworks to interpret delta tuning from the perspective of optimization and optimal control, respectively. Furthermore, we provide a holistic empirical study of representative methods, where results on over 100 NLP tasks demonstrate a comprehensive performance comparison of different approaches. The experimental results also cover the analysis of combinatorial, scaling and transferable properties of delta tuning.

Stochastic Anderson Mixing for Nonconvex Stochastic Optimization

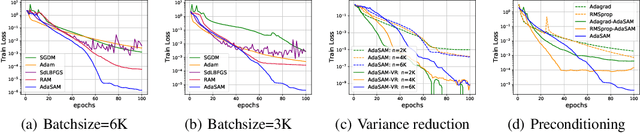
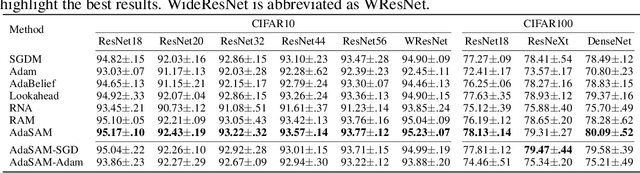
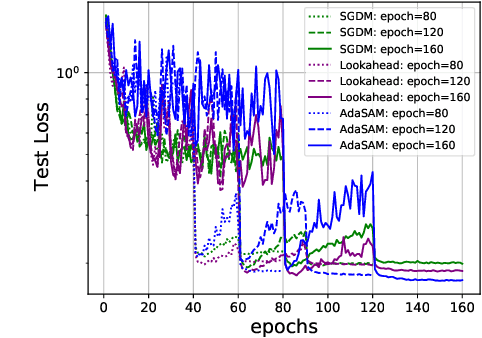
Anderson mixing (AM) is an acceleration method for fixed-point iterations. Despite its success and wide usage in scientific computing, the convergence theory of AM remains unclear, and its applications to machine learning problems are not well explored. In this paper, by introducing damped projection and adaptive regularization to classical AM, we propose a Stochastic Anderson Mixing (SAM) scheme to solve nonconvex stochastic optimization problems. Under mild assumptions, we establish the convergence theory of SAM, including the almost sure convergence to stationary points and the worst-case iteration complexity. Moreover, the complexity bound can be improved when randomly choosing an iterate as the output. To further accelerate the convergence, we incorporate a variance reduction technique into the proposed SAM. We also propose a preconditioned mixing strategy for SAM which can empirically achieve faster convergence or better generalization ability. Finally, we apply the SAM method to train various neural networks including the vanilla CNN, ResNets, WideResNet, ResNeXt, DenseNet and RNN. Experimental results on image classification and language model demonstrate the advantages of our method.