Improved Convex Decomposition with Ensembling and Boolean Primitives

Describing a scene in terms of primitives -- geometrically simple shapes that offer a parsimonious but accurate abstraction of structure -- is an established vision problem. This is a good model of a difficult fitting problem: different scenes require different numbers of primitives and primitives interact strongly, but any proposed solution can be evaluated at inference time. The state of the art method involves a learned regression procedure to predict a start point consisting of a fixed number of primitives, followed by a descent method to refine the geometry and remove redundant primitives. Methods are evaluated by accuracy in depth and normal prediction and in scene segmentation. This paper shows that very significant improvements in accuracy can be obtained by (a) incorporating a small number of negative primitives and (b) ensembling over a number of different regression procedures. Ensembling is by refining each predicted start point, then choosing the best by fitting loss. Extensive experiments on a standard dataset confirm that negative primitives are useful in a large fraction of images, and that our refine-then-choose strategy outperforms choose-then-refine, confirming that the fitting problem is very difficult.

Robust Shape Fitting for 3D Scene Abstraction

Humans perceive and construct the world as an arrangement of simple parametric models. In particular, we can often describe man-made environments using volumetric primitives such as cuboids or cylinders. Inferring these primitives is important for attaining high-level, abstract scene descriptions. Previous approaches for primitive-based abstraction estimate shape parameters directly and are only able to reproduce simple objects. In contrast, we propose a robust estimator for primitive fitting, which meaningfully abstracts complex real-world environments using cuboids. A RANSAC estimator guided by a neural network fits these primitives to a depth map. We condition the network on previously detected parts of the scene, parsing it one-by-one. To obtain cuboids from single RGB images, we additionally optimise a depth estimation CNN end-to-end. Naively minimising point-to-primitive distances leads to large or spurious cuboids occluding parts of the scene. We thus propose an improved occlusion-aware distance metric correctly handling opaque scenes. Furthermore, we present a neural network based cuboid solver which provides more parsimonious scene abstractions while also reducing inference time. The proposed algorithm does not require labour-intensive labels, such as cuboid annotations, for training. Results on the NYU Depth v2 dataset demonstrate that the proposed algorithm successfully abstracts cluttered real-world 3D scene layouts.

PARSAC: Accelerating Robust Multi-Model Fitting with Parallel Sample Consensus

We present a real-time method for robust estimation of multiple instances of geometric models from noisy data. Geometric models such as vanishing points, planar homographies or fundamental matrices are essential for 3D scene analysis. Previous approaches discover distinct model instances in an iterative manner, thus limiting their potential for speedup via parallel computation. In contrast, our method detects all model instances independently and in parallel. A neural network segments the input data into clusters representing potential model instances by predicting multiple sets of sample and inlier weights. Using the predicted weights, we determine the model parameters for each potential instance separately in a RANSAC-like fashion. We train the neural network via task-specific loss functions, i.e. we do not require a ground-truth segmentation of the input data. As suitable training data for homography and fundamental matrix fitting is scarce, we additionally present two new synthetic datasets. We demonstrate state-of-the-art performance on these as well as multiple established datasets, with inference times as small as five milliseconds per image.

Cuboids Revisited: Learning Robust 3D Shape Fitting to Single RGB Images

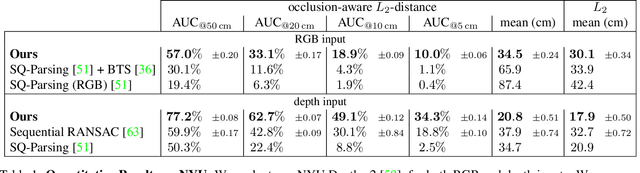
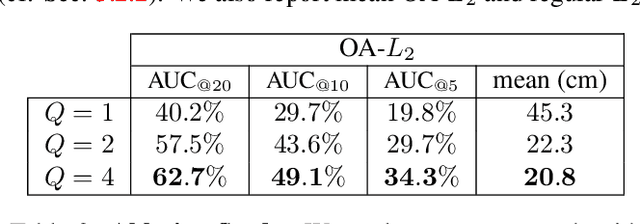
Humans perceive and construct the surrounding world as an arrangement of simple parametric models. In particular, man-made environments commonly consist of volumetric primitives such as cuboids or cylinders. Inferring these primitives is an important step to attain high-level, abstract scene descriptions. Previous approaches directly estimate shape parameters from a 2D or 3D input, and are only able to reproduce simple objects, yet unable to accurately parse more complex 3D scenes. In contrast, we propose a robust estimator for primitive fitting, which can meaningfully abstract real-world environments using cuboids. A RANSAC estimator guided by a neural network fits these primitives to 3D features, such as a depth map. We condition the network on previously detected parts of the scene, thus parsing it one-by-one. To obtain 3D features from a single RGB image, we additionally optimise a feature extraction CNN in an end-to-end manner. However, naively minimising point-to-primitive distances leads to large or spurious cuboids occluding parts of the scene behind. We thus propose an occlusion-aware distance metric correctly handling opaque scenes. The proposed algorithm does not require labour-intensive labels, such as cuboid annotations, for training. Results on the challenging NYU Depth v2 dataset demonstrate that the proposed algorithm successfully abstracts cluttered real-world 3D scene layouts.

CONSAC: Robust Multi-Model Fitting by Conditional Sample Consensus

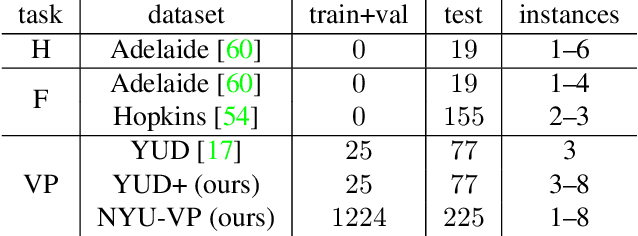
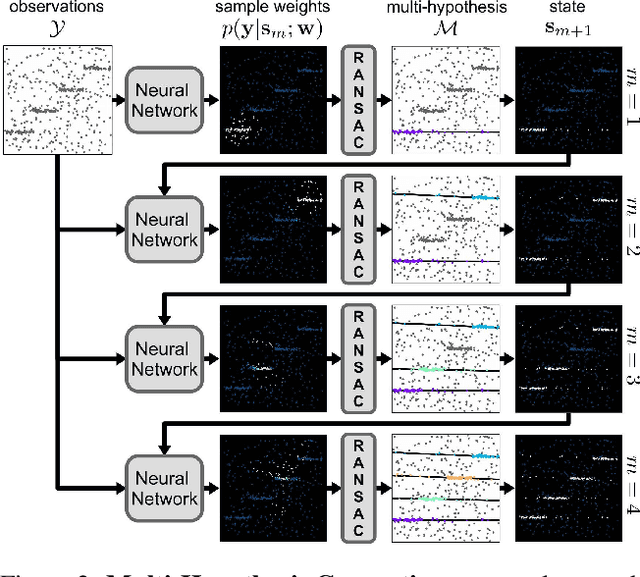
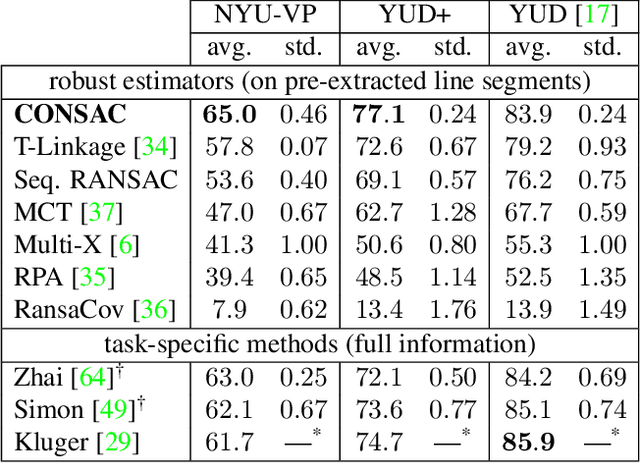
We present a robust estimator for fitting multiple parametric models of the same form to noisy measurements. Applications include finding multiple vanishing points in man-made scenes, fitting planes to architectural imagery, or estimating multiple rigid motions within the same sequence. In contrast to previous works, which resorted to hand-crafted search strategies for multiple model detection, we learn the search strategy from data. A neural network conditioned on previously detected models guides a RANSAC estimator to different subsets of all measurements, thereby finding model instances one after another. We train our method supervised as well as self-supervised. For supervised training of the search strategy, we contribute a new dataset for vanishing point estimation. Leveraging this dataset, the proposed algorithm is superior with respect to other robust estimators as well as to designated vanishing point estimation algorithms. For self-supervised learning of the search, we evaluate the proposed algorithm on multi-homography estimation and demonstrate an accuracy that is superior to state-of-the-art methods.

Temporally Consistent Horizon Lines

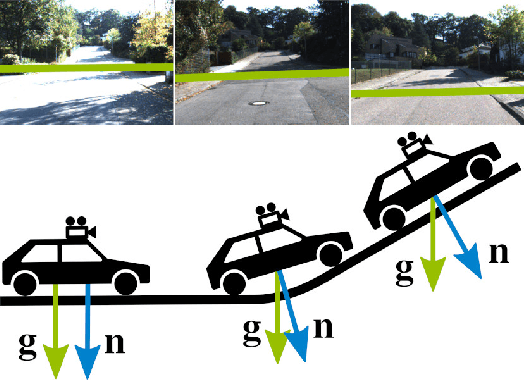
The horizon line is an important geometric feature for many image processing and scene understanding tasks in computer vision. For instance, in navigation of autonomous vehicles or driver assistance, it can be used to improve 3D reconstruction as well as for semantic interpretation of dynamic environments. While both algorithms and datasets exist for single images, the problem of horizon line estimation from video sequences has not gained attention. In this paper, we show how convolutional neural networks are able to utilise the temporal consistency imposed by video sequences in order to increase the accuracy and reduce the variance of horizon line estimates. A novel CNN architecture with an improved residual convolutional LSTM is presented for temporally consistent horizon line estimation. We propose an adaptive loss function that ensures stable training as well as accurate results. Furthermore, we introduce an extension of the KITTI dataset which contains precise horizon line labels for 43699 images across 72 video sequences. A comprehensive evaluation shows that the proposed approach consistently achieves superior performance compared with existing methods.

Deep Learning for Vanishing Point Detection Using an Inverse Gnomonic Projection

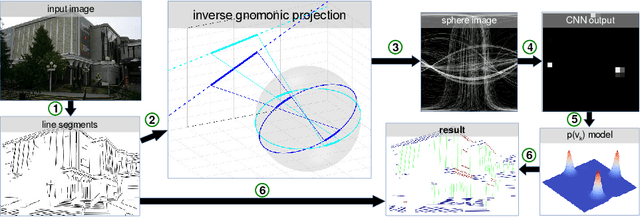
We present a novel approach for vanishing point detection from uncalibrated monocular images. In contrast to state-of-the-art, we make no a priori assumptions about the observed scene. Our method is based on a convolutional neural network (CNN) which does not use natural images, but a Gaussian sphere representation arising from an inverse gnomonic projection of lines detected in an image. This allows us to rely on synthetic data for training, eliminating the need for labelled images. Our method achieves competitive performance on three horizon estimation benchmark datasets. We further highlight some additional use cases for which our vanishing point detection algorithm can be used.