Component-based Sketching for Deep ReLU Nets

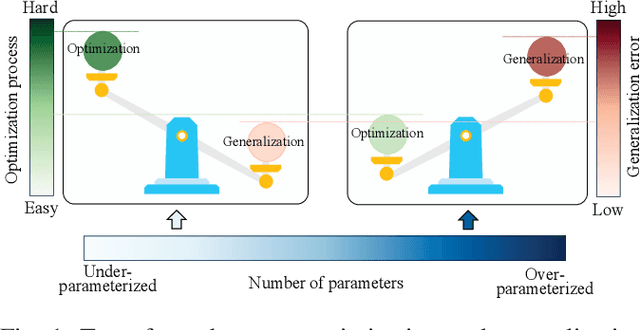
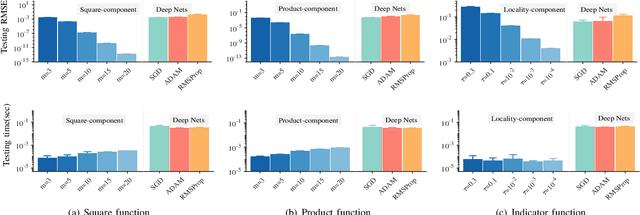
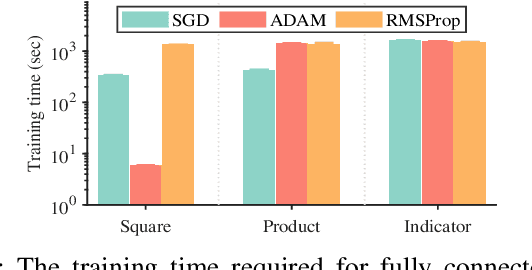
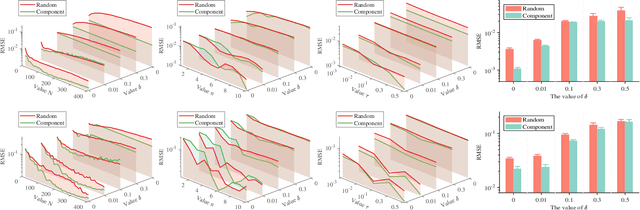
Deep learning has made profound impacts in the domains of data mining and AI, distinguished by the groundbreaking achievements in numerous real-world applications and the innovative algorithm design philosophy. However, it suffers from the inconsistency issue between optimization and generalization, as achieving good generalization, guided by the bias-variance trade-off principle, favors under-parameterized networks, whereas ensuring effective convergence of gradient-based algorithms demands over-parameterized networks. To address this issue, we develop a novel sketching scheme based on deep net components for various tasks. Specifically, we use deep net components with specific efficacy to build a sketching basis that embodies the advantages of deep networks. Subsequently, we transform deep net training into a linear empirical risk minimization problem based on the constructed basis, successfully avoiding the complicated convergence analysis of iterative algorithms. The efficacy of the proposed component-based sketching is validated through both theoretical analysis and numerical experiments. Theoretically, we show that the proposed component-based sketching provides almost optimal rates in approximating saturated functions for shallow nets and also achieves almost optimal generalization error bounds. Numerically, we demonstrate that, compared with the existing gradient-based training methods, component-based sketching possesses superior generalization performance with reduced training costs.

On the Approximation Lower Bound for Neural Nets with Random Weights

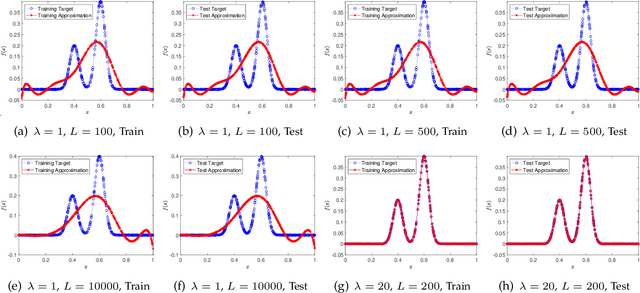
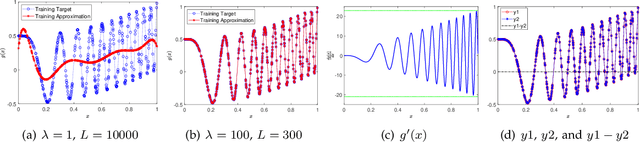
A random net is a shallow neural network where the hidden layer is frozen with random assignment and the output layer is trained by convex optimization. Using random weights for a hidden layer is an effective method to avoid the inevitable non-convexity in standard gradient descent learning. It has recently been adopted in the study of deep learning theory. Here, we investigate the expressive power of random nets. We show that, despite the well-known fact that a shallow neural network is a universal approximator, a random net cannot achieve zero approximation error even for smooth functions. In particular, we prove that for a class of smooth functions, if the proposal distribution is compactly supported, then a lower bound is positive. Based on the ridgelet analysis and harmonic analysis for neural networks, the proof uses the Plancherel theorem and an estimate for the truncated tail of the parameter distribution. We corroborate our theoretical results with various simulation studies, and generally two main take-home messages are offered: (i) Not any distribution for selecting random weights is feasible to build a universal approximator; (ii) A suitable assignment of random weights exists but to some degree is associated with the complexity of the target function.

A study on effectiveness of extreme learning machine

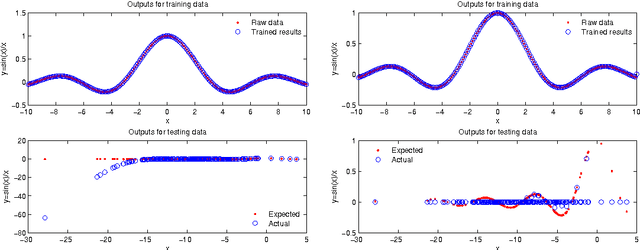
Extreme learning machine (ELM), proposed by Huang et al., has been shown a promising learning algorithm for single-hidden layer feedforward neural networks (SLFNs). Nevertheless, because of the random choice of input weights and biases, the ELM algorithm sometimes makes the hidden layer output matrix H of SLFN not full column rank, which lowers the effectiveness of ELM. This paper discusses the effectiveness of ELM and proposes an improved algorithm called EELM that makes a proper selection of the input weights and bias before calculating the output weights, which ensures the full column rank of H in theory. This improves to some extend the learning rate (testing accuracy, prediction accuracy, learning time) and the robustness property of the networks. The experimental results based on both the benchmark function approximation and real-world problems including classification and regression applications show the good performances of EELM.