Variance-Reduced Model Predictive Path Integral via Quadratic Model Approximation

Sampling-based controllers, such as Model Predictive Path Integral (MPPI) methods, offer substantial flexibility but often suffer from high variance and low sample efficiency. To address these challenges, we introduce a hybrid variance-reduced MPPI framework that integrates a prior model into the sampling process. Our key insight is to decompose the objective function into a known approximate model and a residual term. Since the residual captures only the discrepancy between the model and the objective, it typically exhibits a smaller magnitude and lower variance than the original objective. Although this principle applies to general modeling choices, we demonstrate that adopting a quadratic approximation enables the derivation of a closed-form, model-guided prior that effectively concentrates samples in informative regions. Crucially, the framework is agnostic to the source of geometric information, allowing the quadratic model to be constructed from exact derivatives, structural approximations (e.g., Gauss- or Quasi-Newton), or gradient-free randomized smoothing. We validate the approach on standard optimization benchmarks, a nonlinear, underactuated cart-pole control task, and a contact-rich manipulation problem with non-smooth dynamics. Across these domains, we achieve faster convergence and superior performance in low-sample regimes compared to standard MPPI. These results suggest that the method can make sample-based control strategies more practical in scenarios where obtaining samples is expensive or limited.

KernelSOS for Global Sampling-Based Optimal Control and Estimation via Semidefinite Programming

Global optimization has gained attraction over the past decades, thanks to the development of both theoretical foundations and efficient numerical routines to cope with optimization problems of various complexities. Among recent methods, Kernel Sum of Squares (KernelSOS) appears as a powerful framework, leveraging the potential of sum of squares methods from the polynomial optimization community with the expressivity of kernel methods widely used in machine learning. This paper applies the kernel sum of squares framework for solving control and estimation problems, which exhibit poor local minima. We demonstrate that KernelSOS performs well on a selection of problems from both domains. In particular, we show that KernelSOS is competitive with other sum of squares approaches on estimation problems, while being applicable to non-polynomial and non-parametric formulations. The sample-based nature of KernelSOS allows us to apply it to trajectory optimization problems with an integrated simulator treated as a black box, both as a standalone method and as a powerful initialization method for local solvers, facilitating the discovery of better solutions.

Reactive Stepping for Humanoid Robots using Reinforcement Learning: Application to Standing Push Recovery on the Exoskeleton Atalante

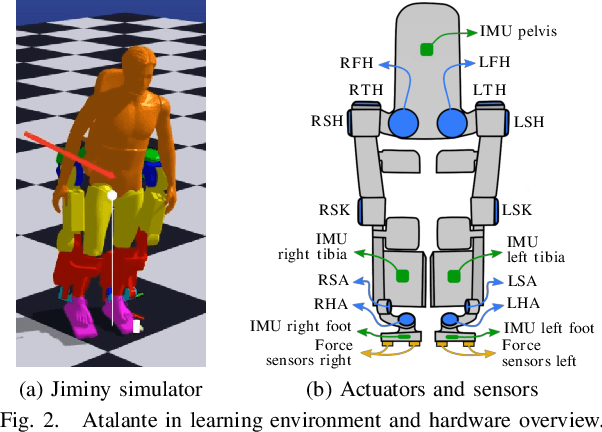
State-of-the-art reinforcement learning is now able to learn versatile locomotion, balancing and push-recovery capabilities for bipedal robots in simulation. Yet, the reality gap has mostly been overlooked and the simulated results hardly transfer to real hardware. Either it is unsuccessful in practice because the physics is over-simplified and hardware limitations are ignored, or regularity is not guaranteed and unexpected hazardous motions can occur. This paper presents a reinforcement learning framework capable of learning robust standing push recovery for bipedal robots with a smooth out-of-the-box transfer to reality, requiring only instantaneous proprioceptive observations. By combining original termination conditions and policy smoothness conditioning, we achieve stable learning, sim-to-real transfer and safety using a policy without memory nor observation history. Reward shaping is then used to give insights into how to keep balance. We demonstrate its performance in reality on the lower-limb medical exoskeleton Atalante.