Evan Patterson
Automating Transfer of Robot Task Plans using Functorial Data Migrations
Jun 22, 2024Abstract:This paper introduces a novel approach to ontology-based robot plan transfer using functorial data migrations from category theory. Functors provide structured maps between domain types and predicates which can be used to transfer plans from a source domain to a target domain without the need for replanning. Unlike methods that create models for transferring specific plans, our approach can be applied to any plan within a given domain. We demonstrate this approach by transferring a task plan from the canonical Blocksworld domain to one compatible with the AI2-THOR Kitchen environment. In addition, we discuss practical applications that may enhance the adaptability of robotic task planning in general.
A Categorical Representation Language and Computational System for Knowledge-Based Planning
May 26, 2023Abstract:Classical planning representation languages based on first-order logic have been extensively used to model and solve planning problems, but they struggle to capture implicit preconditions and effects that arise in complex planning scenarios. To address this problem, we propose an alternative approach to representing and transforming world states during planning. Based on the category-theoretic concepts of $\mathsf{C}$-sets and double-pushout rewriting (DPO), our proposed representation can effectively handle structured knowledge about world states that support domain abstractions at all levels. It formalizes the semantics of predicates according to a user-provided ontology and preserves the semantics when transitioning between world states. This method provides a formal semantics for using knowledge graphs and relational databases to model world states and updates in planning. In this paper, we compare our category-theoretic representation with the classical planning representation. We show that our proposed representation has advantages over the classical representation in terms of handling implicit preconditions and effects, and provides a more structured framework in which to model and solve planning problems.
String Diagrams for Assembly Planning
Sep 23, 2019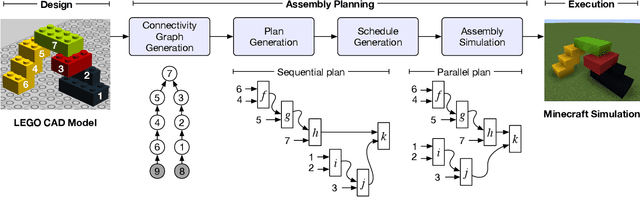
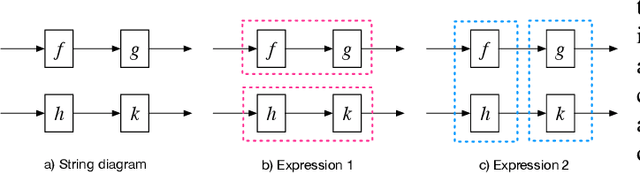
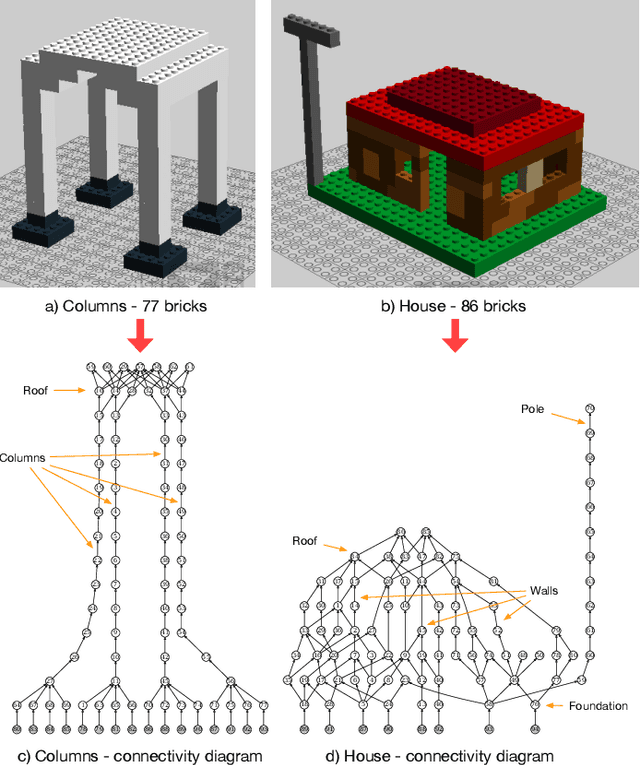
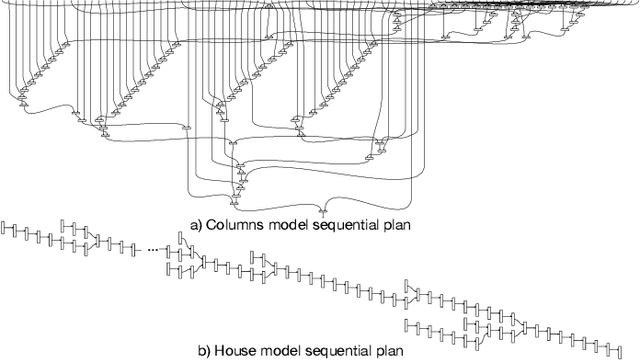
Abstract:Assembly planning is a difficult problem for companies. Many disciplines such as design, planning, scheduling, and manufacturing execution need to be carefully engineered and coordinated to create successful product assembly plans. Recent research in the field of design for assembly has proposed new methodologies to design product structures in such a way that their assembly is easier. However, present assembly planning approaches lack the engineering tool support to capture all the constraints associated to assembly planning in a unified manner. This paper proposes CompositionalPlanning, a string diagram based framework for assembly planning. In the proposed framework, string diagrams and their compositional properties serve as the foundation for an engineering tool where CAD designs interact with planning and scheduling algorithms to automatically create high-quality assembly plans. These assembly plans are then executed in simulation to measure their performance and to visualize their key build characteristics. We demonstrate the versatility of this approach in the LEGO assembly domain. We developed two reference LEGO CAD models that are processed by CompositionalPlanning's algorithmic pipeline. We compare sequential and parallel assembly plans in a Minecraft simulation and show that the time-to-build performance can be optimized by our algorithms.
Graph Representation Ensemble Learning
Sep 12, 2019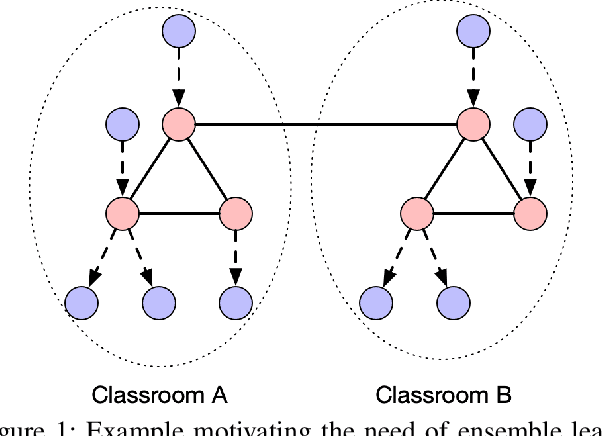
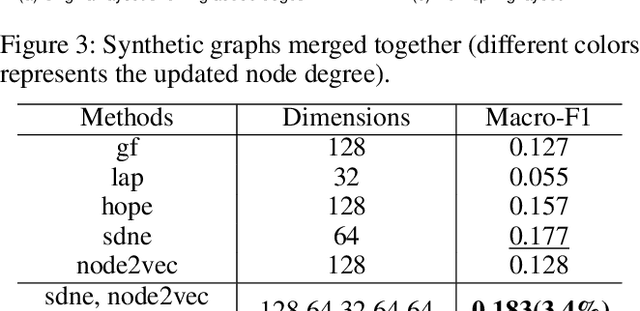
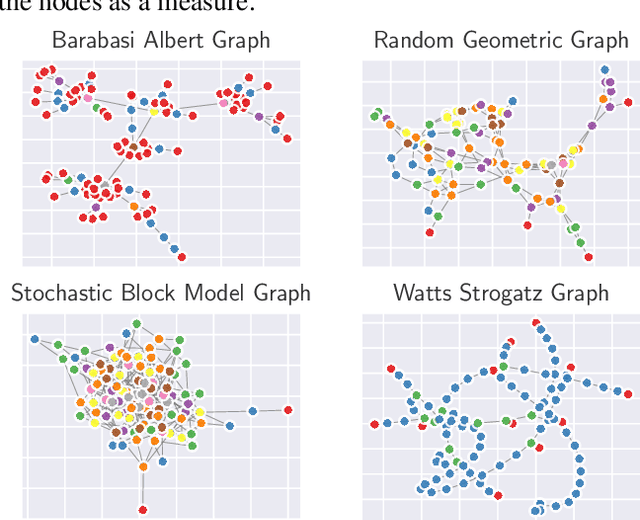
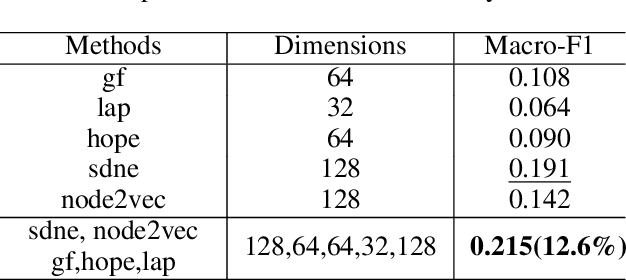
Abstract:Representation learning on graphs has been gaining attention due to its wide applicability in predicting missing links, and classifying and recommending nodes. Most embedding methods aim to preserve certain properties of the original graph in the low dimensional space. However, real world graphs have a combination of several properties which are difficult to characterize and capture by a single approach. In this work, we introduce the problem of graph representation ensemble learning and provide a first of its kind framework to aggregate multiple graph embedding methods efficiently. We provide analysis of our framework and analyze -- theoretically and empirically -- the dependence between state-of-the-art embedding methods. We test our models on the node classification task on four real world graphs and show that proposed ensemble approaches can outperform the state-of-the-art methods by up to 8% on macro-F1. We further show that the approach is even more beneficial for underrepresented classes providing an improvement of up to 12%.
Conformalized Quantile Regression
May 08, 2019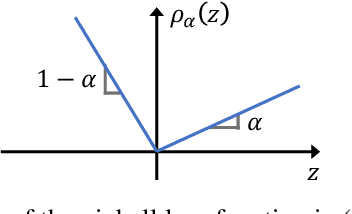
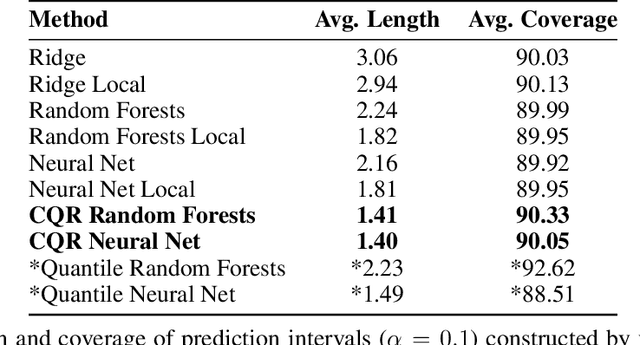
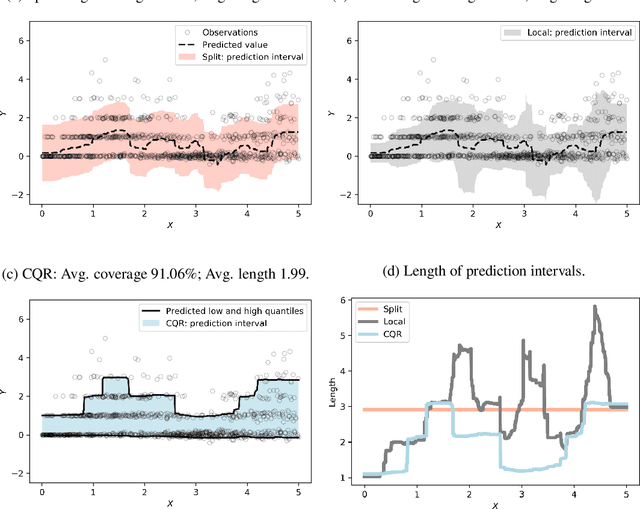
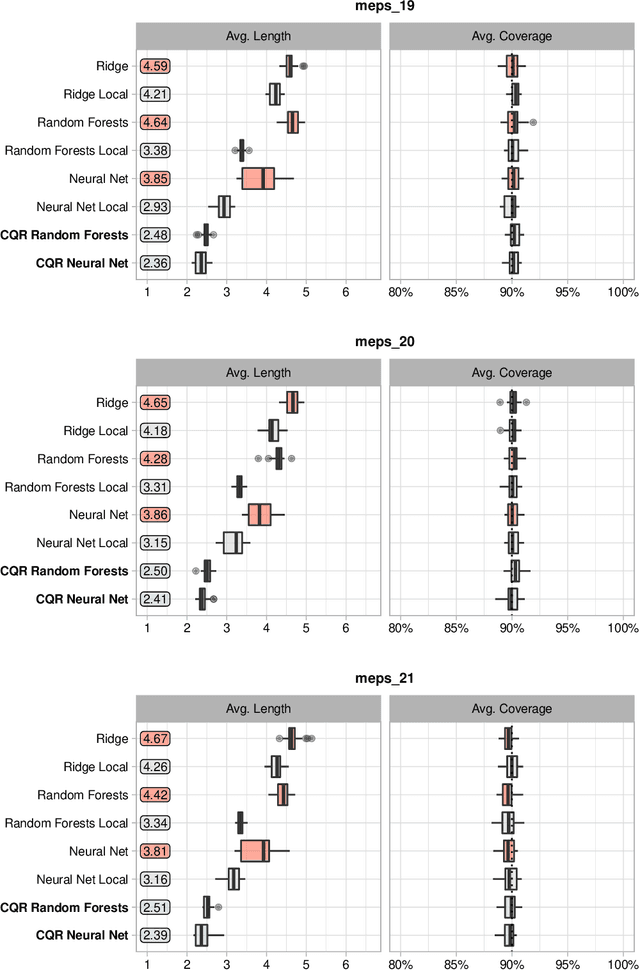
Abstract:Conformal prediction is a technique for constructing prediction intervals that attain valid coverage in finite samples, without making distributional assumptions. Despite this appeal, existing conformal methods can be unnecessarily conservative because they form intervals of constant or weakly varying length across the input space. In this paper we propose a new method that is fully adaptive to heteroscedasticity. It combines conformal prediction with classical quantile regression, inheriting the advantages of both. We establish a theoretical guarantee of valid coverage, supplemented by extensive experiments on popular regression datasets. We compare the efficiency of conformalized quantile regression to other conformal methods, showing that our method tends to produce shorter intervals.
Teaching machines to understand data science code by semantic enrichment of dataflow graphs
Jul 16, 2018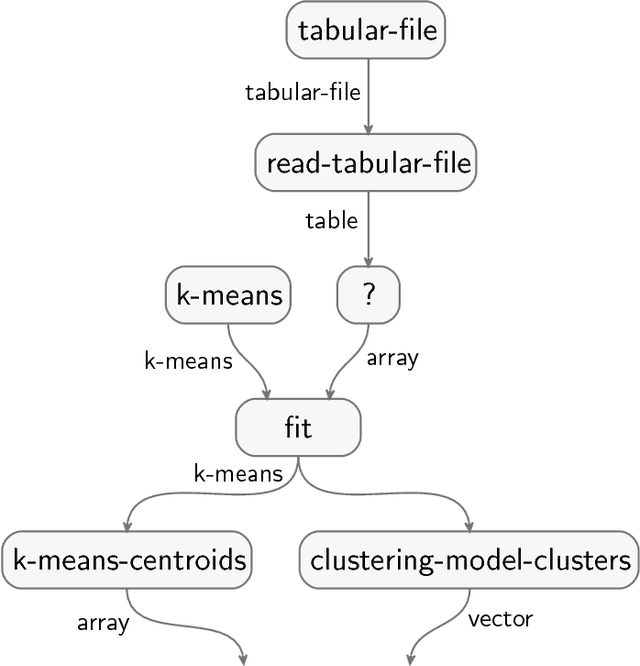

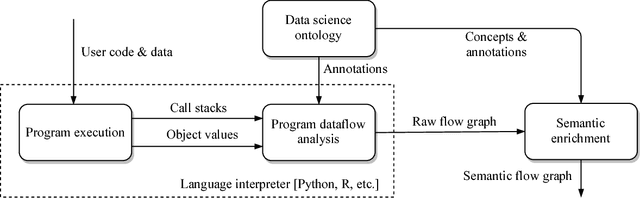
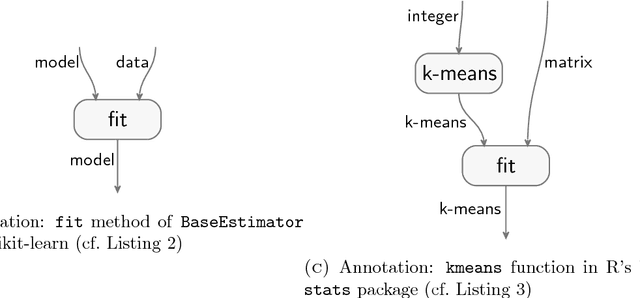
Abstract:Your computer is continuously executing programs, but does it really understand them? Not in any meaningful sense. That burden falls upon human knowledge workers, who are increasingly asked to write and understand code. They would benefit greatly from intelligent tools that reveal the connections between their code and its subject matter. Towards this prospect, we develop an AI system that forms semantic representations of computer programs, using techniques from knowledge representation and program analysis. We focus on code written for data science, although our method is more generally applicable. The semantic representations are created through a novel algorithm for the semantic enrichment of dataflow graphs. This algorithm is undergirded by a new ontology language for modeling computer programs and a new ontology about data science, written in this language.
Knowledge Representation in Bicategories of Relations
Nov 01, 2017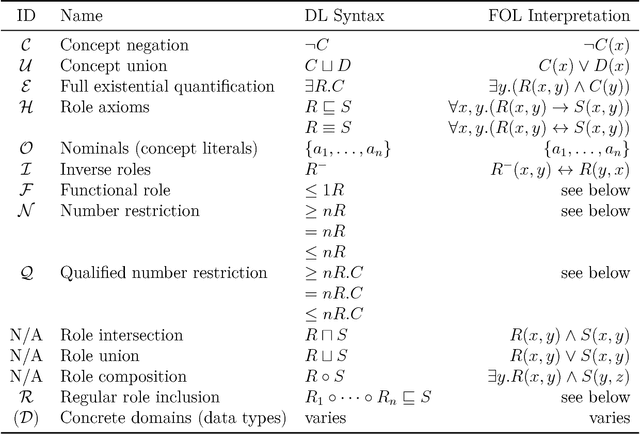


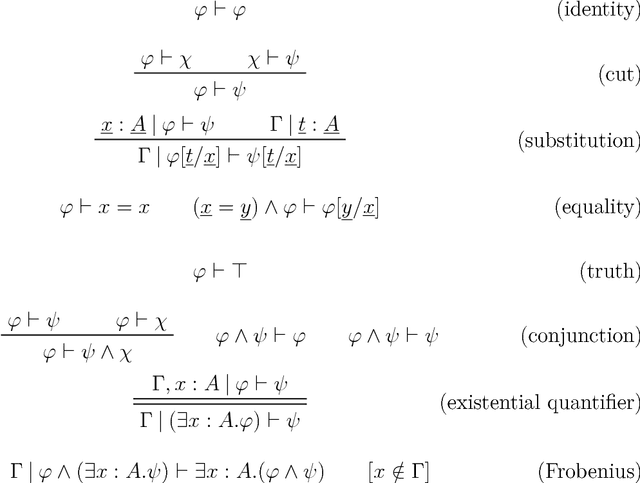
Abstract:We introduce the relational ontology log, or relational olog, a knowledge representation system based on the category of sets and relations. It is inspired by Spivak and Kent's olog, a recent categorical framework for knowledge representation. Relational ologs interpolate between ologs and description logic, the dominant formalism for knowledge representation today. In this paper, we investigate relational ologs both for their own sake and to gain insight into the relationship between the algebraic and logical approaches to knowledge representation. On a practical level, we show by example that relational ologs have a friendly and intuitive--yet fully precise--graphical syntax, derived from the string diagrams of monoidal categories. We explain several other useful features of relational ologs not possessed by most description logics, such as a type system and a rich, flexible notion of instance data. In a more theoretical vein, we draw on categorical logic to show how relational ologs can be translated to and from logical theories in a fragment of first-order logic. Although we make extensive use of categorical language, this paper is designed to be self-contained and has considerable expository content. The only prerequisites are knowledge of first-order logic and the rudiments of category theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge