Automating Transfer of Robot Task Plans using Functorial Data Migrations

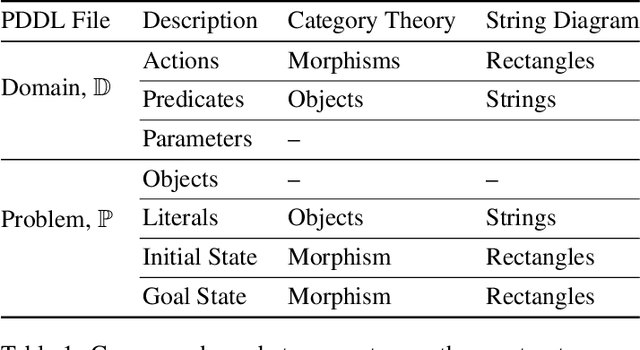
This paper introduces a novel approach to ontology-based robot plan transfer using functorial data migrations from category theory. Functors provide structured maps between domain types and predicates which can be used to transfer plans from a source domain to a target domain without the need for replanning. Unlike methods that create models for transferring specific plans, our approach can be applied to any plan within a given domain. We demonstrate this approach by transferring a task plan from the canonical Blocksworld domain to one compatible with the AI2-THOR Kitchen environment. In addition, we discuss practical applications that may enhance the adaptability of robotic task planning in general.

A Categorical Representation Language and Computational System for Knowledge-Based Planning

Classical planning representation languages based on first-order logic have been extensively used to model and solve planning problems, but they struggle to capture implicit preconditions and effects that arise in complex planning scenarios. To address this problem, we propose an alternative approach to representing and transforming world states during planning. Based on the category-theoretic concepts of $\mathsf{C}$-sets and double-pushout rewriting (DPO), our proposed representation can effectively handle structured knowledge about world states that support domain abstractions at all levels. It formalizes the semantics of predicates according to a user-provided ontology and preserves the semantics when transitioning between world states. This method provides a formal semantics for using knowledge graphs and relational databases to model world states and updates in planning. In this paper, we compare our category-theoretic representation with the classical planning representation. We show that our proposed representation has advantages over the classical representation in terms of handling implicit preconditions and effects, and provides a more structured framework in which to model and solve planning problems.

Encoding Compositionality in Classical Planning Solutions

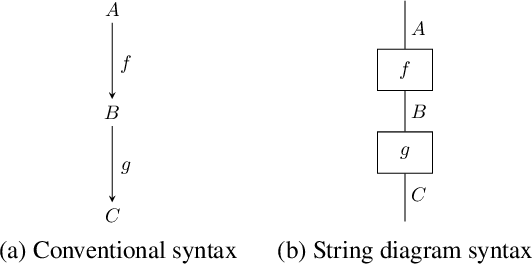
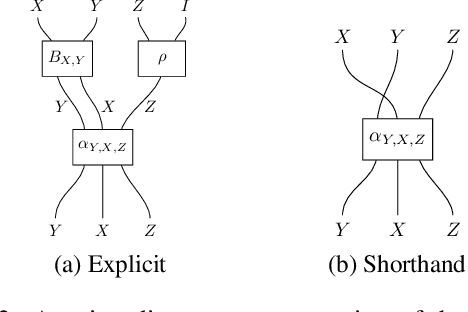
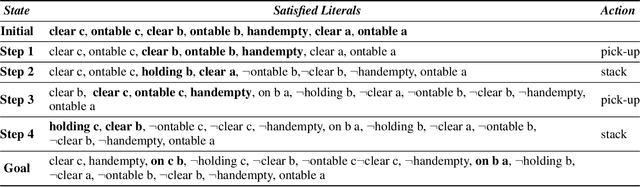
Classical AI planners provide solutions to planning problems in the form of long and opaque text outputs. To aid in the understanding transferability of planning solutions, it is necessary to have a rich and comprehensible representation for both human and computers beyond the current line-by-line text notation. In particular, it is desirable to encode the trace of literals throughout the plan to capture the dependencies between actions selected. The approach of this paper is to view the actions as maps between literals and the selected plan as a composition of those maps. The mathematical theory, called category theory, provides the relevant structures for capturing maps, their compositions, and maps between compositions. We employ this theory to propose an algorithm agnostic, model-based representation for domains, problems, and plans expressed in the commonly used planning description language, PDDL. This category theoretic representation is accompanied by a graphical syntax in addition to a linear notation, similar to algebraic expressions, that can be used to infer literals used at every step of the plan. This provides the appropriate constructive abstraction and facilitates comprehension for human operators. In this paper, we demonstrate this on a plan within the Blocksworld domain.

Compressing GANs using Knowledge Distillation

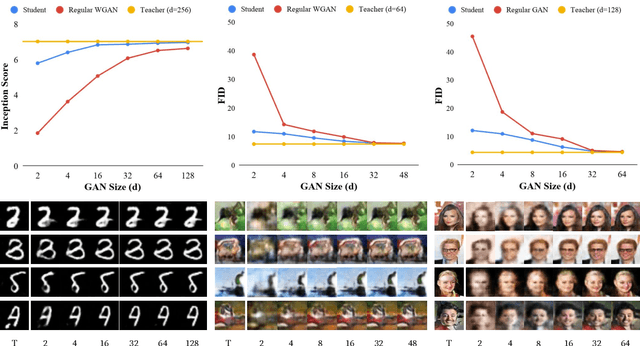
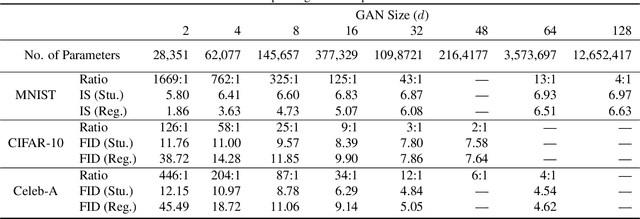
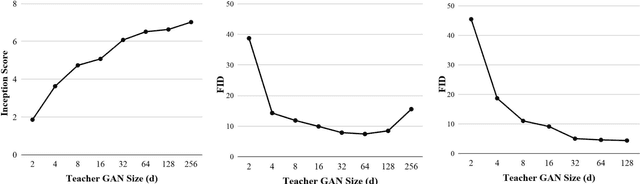
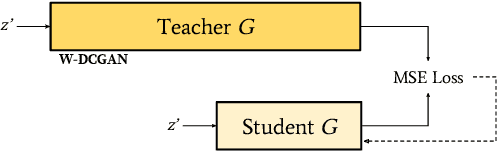
Generative Adversarial Networks (GANs) have been used in several machine learning tasks such as domain transfer, super resolution, and synthetic data generation. State-of-the-art GANs often use tens of millions of parameters, making them expensive to deploy for applications in low SWAP (size, weight, and power) hardware, such as mobile devices, and for applications with real time capabilities. There has been no work found to reduce the number of parameters used in GANs. Therefore, we propose a method to compress GANs using knowledge distillation techniques, in which a smaller "student" GAN learns to mimic a larger "teacher" GAN. We show that the distillation methods used on MNIST, CIFAR-10, and Celeb-A datasets can compress teacher GANs at ratios of 1669:1, 58:1, and 87:1, respectively, while retaining the quality of the generated image. From our experiments, we observe a qualitative limit for GAN's compression. Moreover, we observe that, with a fixed parameter budget, compressed GANs outperform GANs trained using standard training methods. We conjecture that this is partially owing to the optimization landscape of over-parameterized GANs which allows efficient training using alternating gradient descent. Thus, training an over-parameterized GAN followed by our proposed compression scheme provides a high quality generative model with a small number of parameters.