Conditional Sampling from Invertible Generative Models with Applications to Inverse Problems

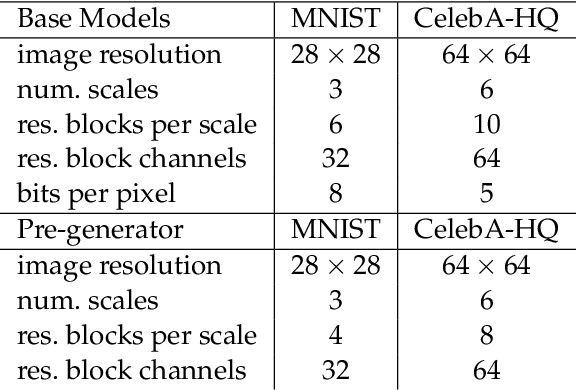
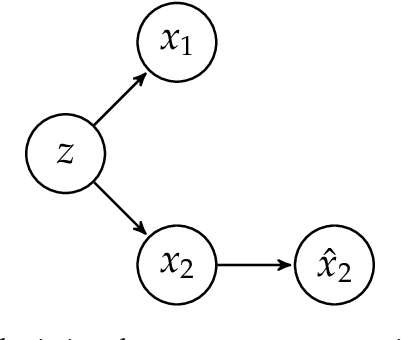
We consider uncertainty aware compressive sensing when the prior distribution is defined by an invertible generative model. In this problem, we receive a set of low dimensional measurements and we want to generate conditional samples of high dimensional objects conditioned on these measurements. We first show that the conditional sampling problem is hard in general, and thus we consider approximations to the problem. We develop a variational approach to conditional sampling that composes a new generative model with the given generative model. This allows us to utilize the sampling ability of the given generative model to quickly generate samples from the conditional distribution.

Experimental Design for Cost-Aware Learning of Causal Graphs

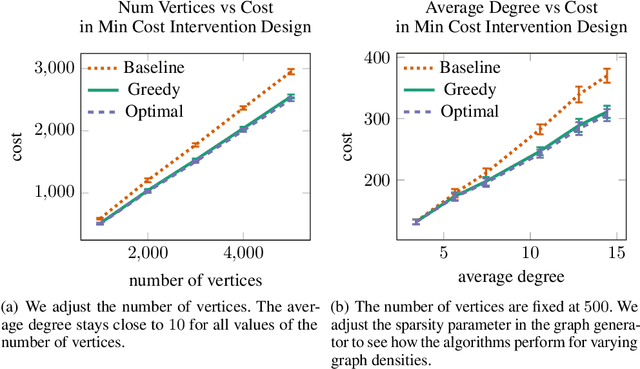
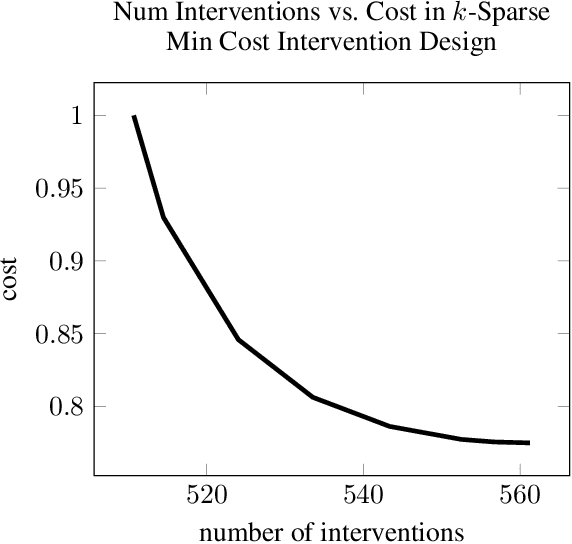
We consider the minimum cost intervention design problem: Given the essential graph of a causal graph and a cost to intervene on a variable, identify the set of interventions with minimum total cost that can learn any causal graph with the given essential graph. We first show that this problem is NP-hard. We then prove that we can achieve a constant factor approximation to this problem with a greedy algorithm. We then constrain the sparsity of each intervention. We develop an algorithm that returns an intervention design that is nearly optimal in terms of size for sparse graphs with sparse interventions and we discuss how to use it when there are costs on the vertices.

Leveraging Sparsity for Efficient Submodular Data Summarization

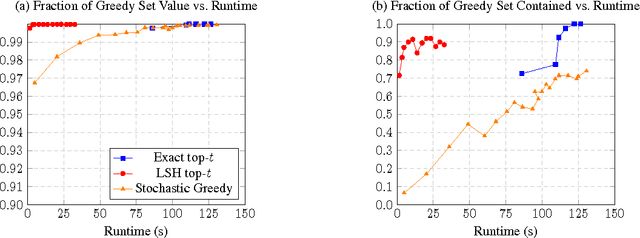
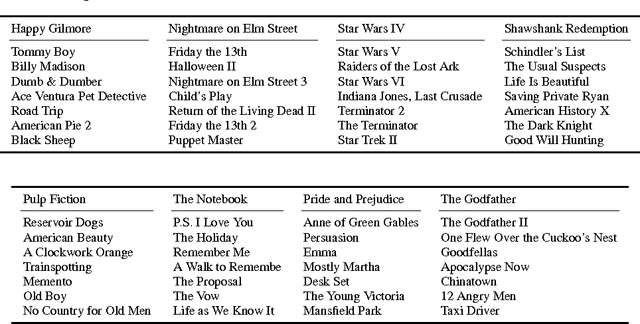
The facility location problem is widely used for summarizing large datasets and has additional applications in sensor placement, image retrieval, and clustering. One difficulty of this problem is that submodular optimization algorithms require the calculation of pairwise benefits for all items in the dataset. This is infeasible for large problems, so recent work proposed to only calculate nearest neighbor benefits. One limitation is that several strong assumptions were invoked to obtain provable approximation guarantees. In this paper we establish that these extra assumptions are not necessary---solving the sparsified problem will be almost optimal under the standard assumptions of the problem. We then analyze a different method of sparsification that is a better model for methods such as Locality Sensitive Hashing to accelerate the nearest neighbor computations and extend the use of the problem to a broader family of similarities. We validate our approach by demonstrating that it rapidly generates interpretable summaries.

Exact MAP Inference by Avoiding Fractional Vertices

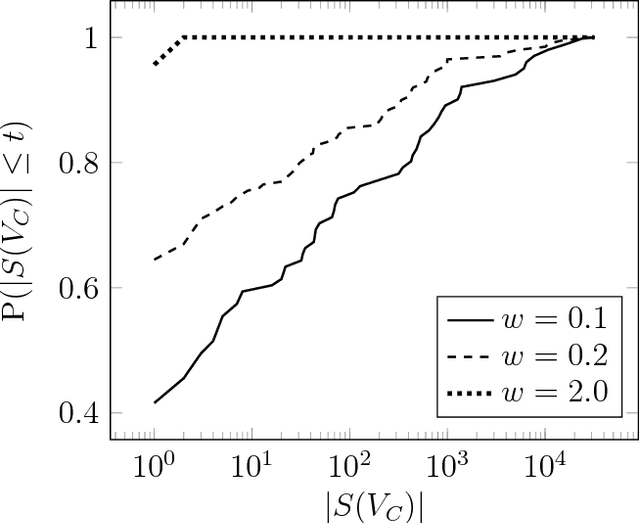
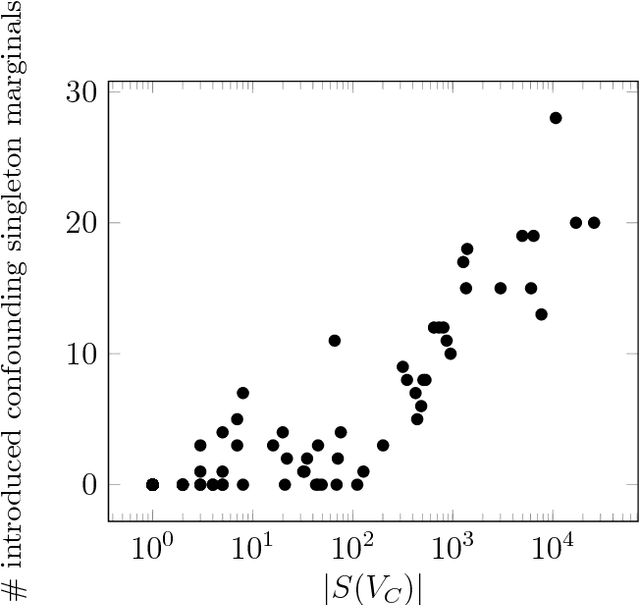
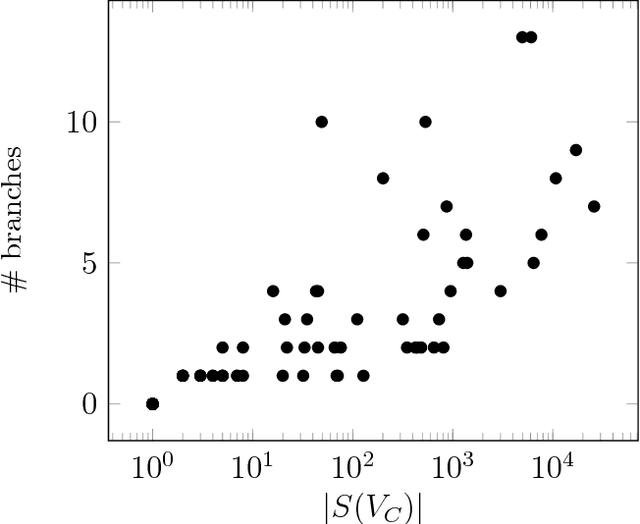
Given a graphical model, one essential problem is MAP inference, that is, finding the most likely configuration of states according to the model. Although this problem is NP-hard, large instances can be solved in practice. A major open question is to explain why this is true. We give a natural condition under which we can provably perform MAP inference in polynomial time. We require that the number of fractional vertices in the LP relaxation exceeding the optimal solution is bounded by a polynomial in the problem size. This resolves an open question by Dimakis, Gohari, and Wainwright. In contrast, for general LP relaxations of integer programs, known techniques can only handle a constant number of fractional vertices whose value exceeds the optimal solution. We experimentally verify this condition and demonstrate how efficient various integer programming methods are at removing fractional solutions.