Exact MAP Inference by Avoiding Fractional Vertices
Paper and Code
Mar 08, 2017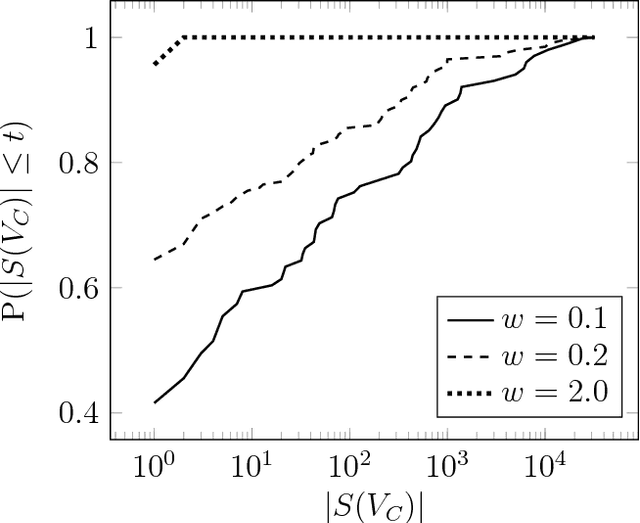
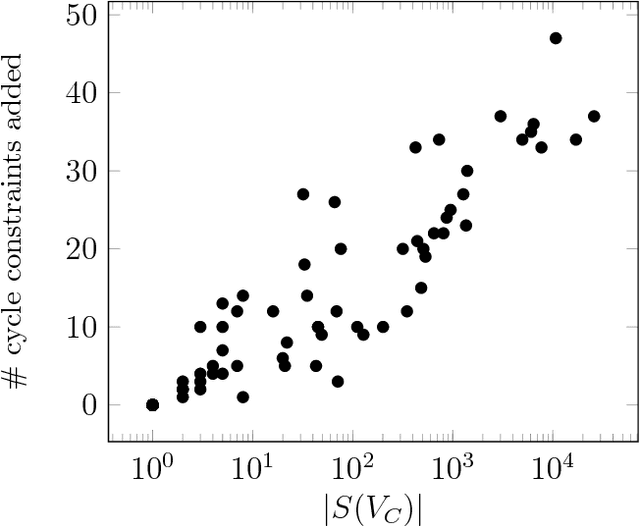
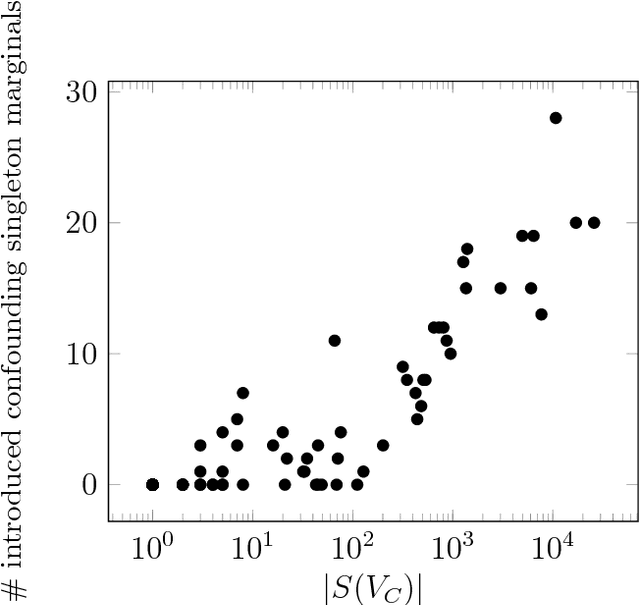
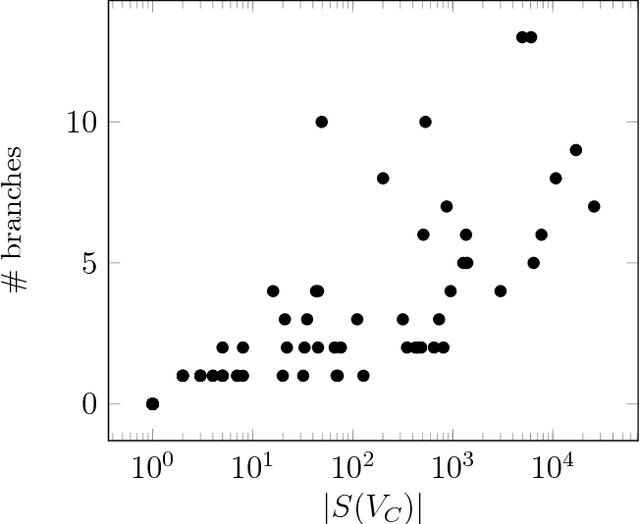
Given a graphical model, one essential problem is MAP inference, that is, finding the most likely configuration of states according to the model. Although this problem is NP-hard, large instances can be solved in practice. A major open question is to explain why this is true. We give a natural condition under which we can provably perform MAP inference in polynomial time. We require that the number of fractional vertices in the LP relaxation exceeding the optimal solution is bounded by a polynomial in the problem size. This resolves an open question by Dimakis, Gohari, and Wainwright. In contrast, for general LP relaxations of integer programs, known techniques can only handle a constant number of fractional vertices whose value exceeds the optimal solution. We experimentally verify this condition and demonstrate how efficient various integer programming methods are at removing fractional solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge