Conditional Sampling from Invertible Generative Models with Applications to Inverse Problems

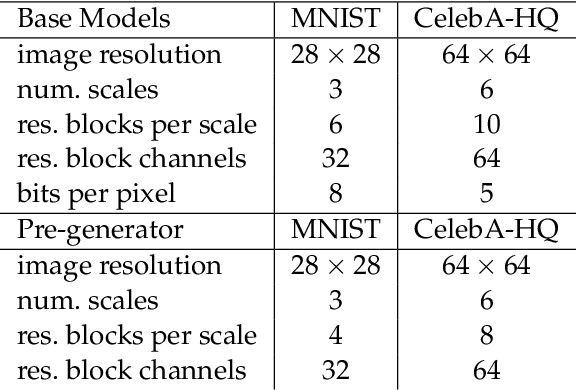
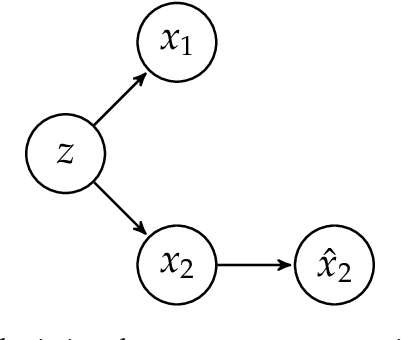
We consider uncertainty aware compressive sensing when the prior distribution is defined by an invertible generative model. In this problem, we receive a set of low dimensional measurements and we want to generate conditional samples of high dimensional objects conditioned on these measurements. We first show that the conditional sampling problem is hard in general, and thus we consider approximations to the problem. We develop a variational approach to conditional sampling that composes a new generative model with the given generative model. This allows us to utilize the sampling ability of the given generative model to quickly generate samples from the conditional distribution.