Spatially Regularized Super-Resolved Constrained Spherical Deconvolution (SR$^2$-CSD) of Diffusion MRI Data

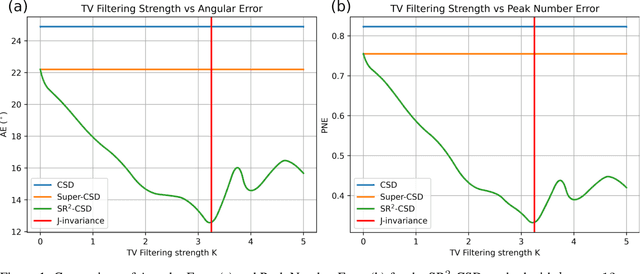
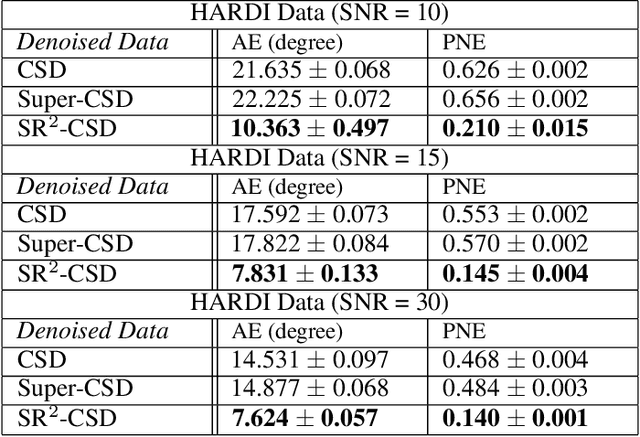
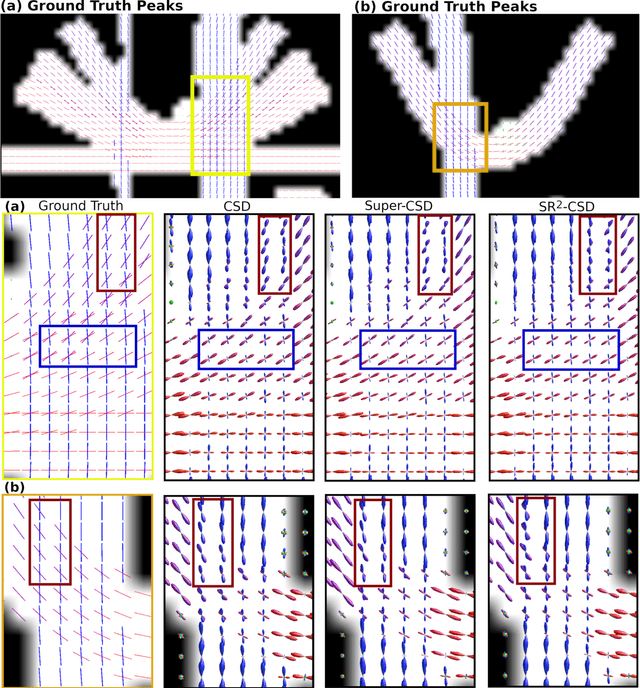
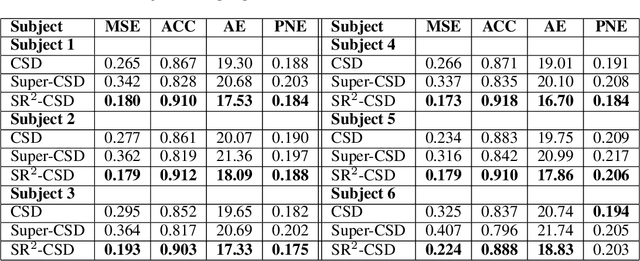
Constrained Spherical Deconvolution (CSD) is crucial for estimating white matter fiber orientations using diffusion MRI data. A relevant parameter in CSD is the maximum order $l_{max}$ used in the spherical harmonics series, influencing the angular resolution of the Fiber Orientation Distributions (FODs). Lower $l_{max}$ values produce smoother and more stable estimates, but result in reduced angular resolution. Conversely, higher $l_{max}$ values, as employed in the Super-Resolved CSD variant, are essential for resolving narrow inter-fiber angles but lead to spurious lobes due to increased noise sensitivity. To address this issue, we propose a novel Spatially Regularized Super-Resolved CSD (SR$^2$-CSD) approach, incorporating spatial priors into the CSD framework. This method leverages spatial information among adjacent voxels, enhancing the stability and noise robustness of FOD estimations. SR$^2$-CSD facilitates the practical use of Super-Resolved CSD by including a J-invariant auto-calibrated total variation FOD denoiser. We evaluated the performance of SR$^2$-CSD against standard CSD and Super-Resolved CSD using phantom numerical data and various real brain datasets, including a test-retest sample of six subjects scanned twice. In phantom data, SR$^2$-CSD outperformed both CSD and Super-Resolved CSD, reducing the angular error (AE) by approximately half and the peak number error (PNE) by a factor of three across all noise levels considered. In real data, SR$^2$-CSD produced more continuous FOD estimates with higher spatial-angular coherency. In the test-retest sample, SR$^2$-CSD consistently yielded more reproducible estimates, with reduced AE, PNE, mean squared error, and increased angular correlation coefficient between the FODs estimated from the two scans for each subject.

Axial and radial axonal diffusivities from single encoding strongly diffusion-weighted MRI

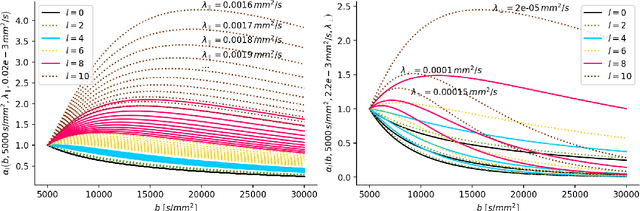
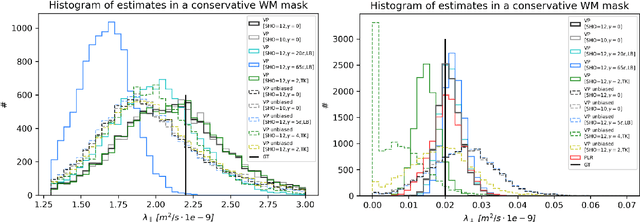
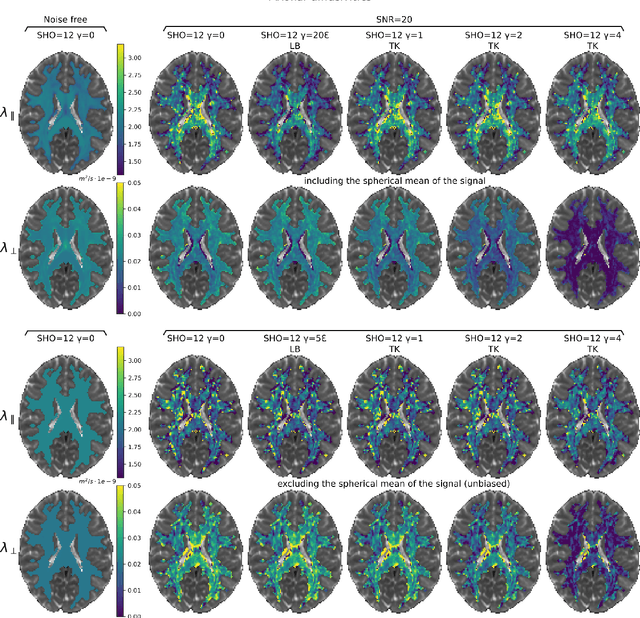
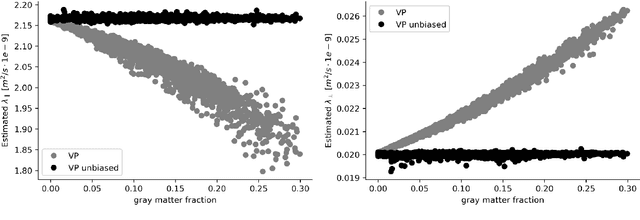
We enable the estimation of the per-axon axial diffusivity from single encoding, strongly diffusion-weighted, pulsed gradient spin echo data. Additionally, we improve the estimation of the per-axon radial diffusivity compared to estimates based on spherical averaging. The use of strong diffusion weightings in magnetic resonance imaging (MRI) allows to approximate the signal in white matter as the sum of the contributions from axons. At the same time, spherical averaging leads to a major simplification of the modeling by removing the need to explicitly account for the unknown orientation distribution of axons. However, the spherically averaged signal acquired at strong diffusion weightings is not sensitive to the axial diffusivity, which cannot therefore be estimated. After revising existing theory, we introduce a new general method for the estimation of both axonal diffusivities at strong diffusion weightings based on zonal harmonics modeling. We additionally show how this could lead to estimates that are free from partial volume bias with, for instance, gray matter. We test the method on publicly available data from the MGH Adult Diffusion Human Connectome project dataset. We report reference values of axonal diffusivities based on 34 subjects, and derive estimates of axonal radii. We address the estimation problem also from the angle of the required data preprocessing, the presence of biases related to modeling assumptions, current limitations, and future possibilities.

Validation and Generalizability of Self-Supervised Image Reconstruction Methods for Undersampled MRI

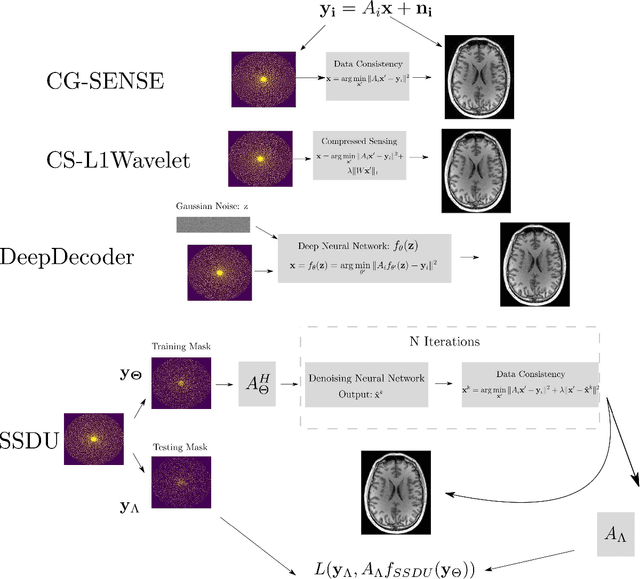
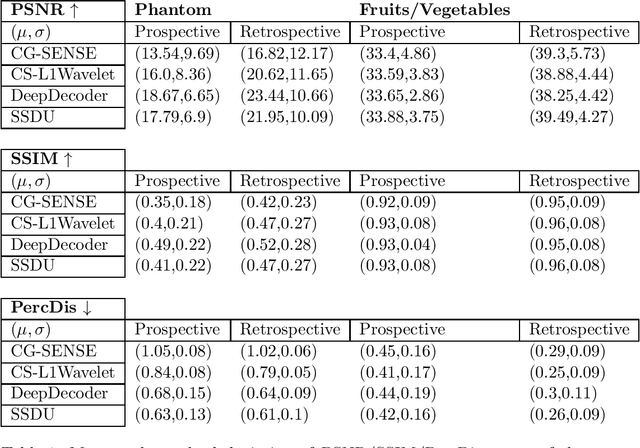
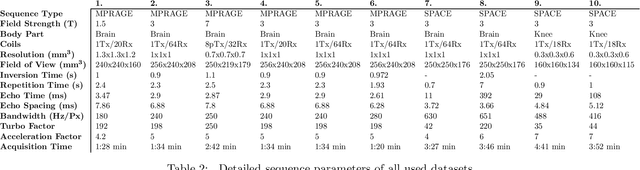
Purpose: To investigate aspects of the validation of self-supervised algorithms for reconstruction of undersampled MR images: quantitative evaluation of prospective reconstructions, potential differences between prospective and retrospective reconstructions, suitability of commonly used quantitative metrics, and generalizability. Theory and Methods: Two self-supervised algorithms based on self-supervised denoising and neural network image priors were investigated. These methods are compared to a least squares fitting and a compressed sensing reconstruction using in-vivo and phantom data. Their generalizability was tested with prospectively under-sampled data from experimental conditions different to the training. Results: Prospective reconstructions can exhibit significant distortion relative to retrospective reconstructions/ground truth. Pixel-wise quantitative metrics may not capture differences in perceptual quality accurately, in contrast to a perceptual metric. All methods showed potential for generalization; generalizability is more affected by changes in anatomy/contrast than other changes. No-reference image metrics correspond well with human rating of image quality for studying generalizability. Compressed Sensing and learned denoising perform similarly well on all data. Conclusion: Self-supervised methods show promising results for accelerating image reconstruction in clinical routines. Nonetheless, more work is required to investigate standardized methods to validate reconstruction algorithms for future clinical use.