Spatially Regularized Super-Resolved Constrained Spherical Deconvolution (SR$^2$-CSD) of Diffusion MRI Data
Paper and Code
Aug 23, 2024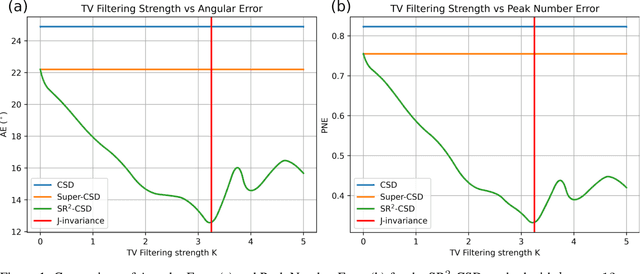
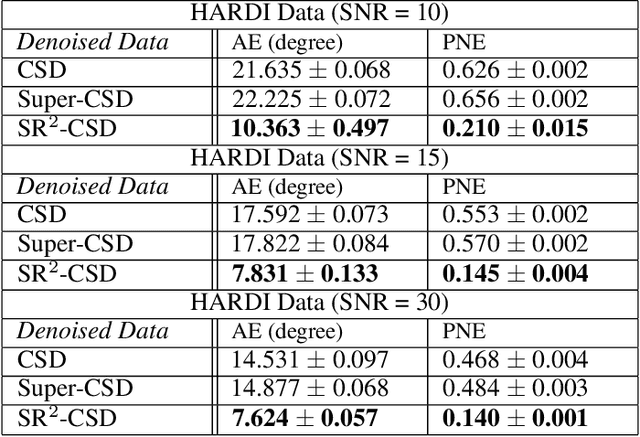
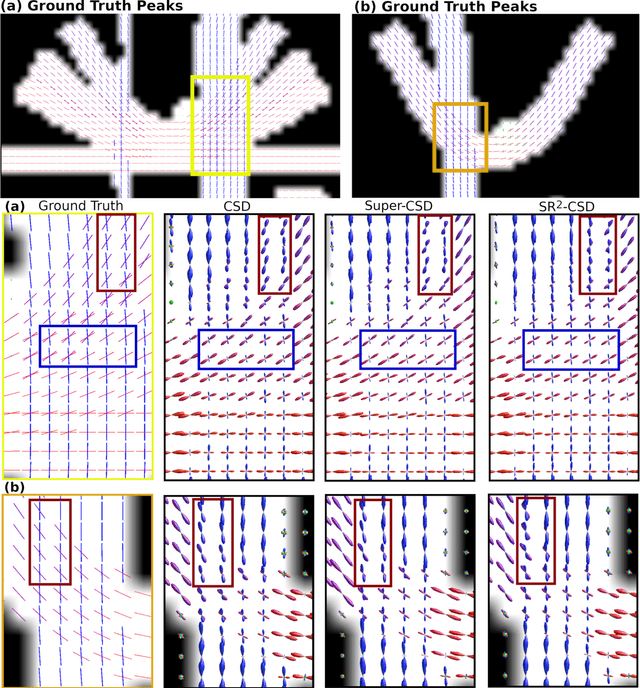
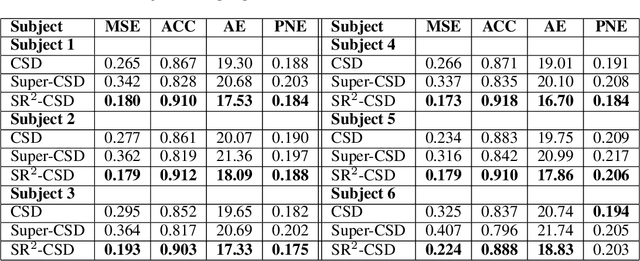
Constrained Spherical Deconvolution (CSD) is crucial for estimating white matter fiber orientations using diffusion MRI data. A relevant parameter in CSD is the maximum order $l_{max}$ used in the spherical harmonics series, influencing the angular resolution of the Fiber Orientation Distributions (FODs). Lower $l_{max}$ values produce smoother and more stable estimates, but result in reduced angular resolution. Conversely, higher $l_{max}$ values, as employed in the Super-Resolved CSD variant, are essential for resolving narrow inter-fiber angles but lead to spurious lobes due to increased noise sensitivity. To address this issue, we propose a novel Spatially Regularized Super-Resolved CSD (SR$^2$-CSD) approach, incorporating spatial priors into the CSD framework. This method leverages spatial information among adjacent voxels, enhancing the stability and noise robustness of FOD estimations. SR$^2$-CSD facilitates the practical use of Super-Resolved CSD by including a J-invariant auto-calibrated total variation FOD denoiser. We evaluated the performance of SR$^2$-CSD against standard CSD and Super-Resolved CSD using phantom numerical data and various real brain datasets, including a test-retest sample of six subjects scanned twice. In phantom data, SR$^2$-CSD outperformed both CSD and Super-Resolved CSD, reducing the angular error (AE) by approximately half and the peak number error (PNE) by a factor of three across all noise levels considered. In real data, SR$^2$-CSD produced more continuous FOD estimates with higher spatial-angular coherency. In the test-retest sample, SR$^2$-CSD consistently yielded more reproducible estimates, with reduced AE, PNE, mean squared error, and increased angular correlation coefficient between the FODs estimated from the two scans for each subject.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge