Maximum Consensus by Weighted Influences of Monotone Boolean Functions

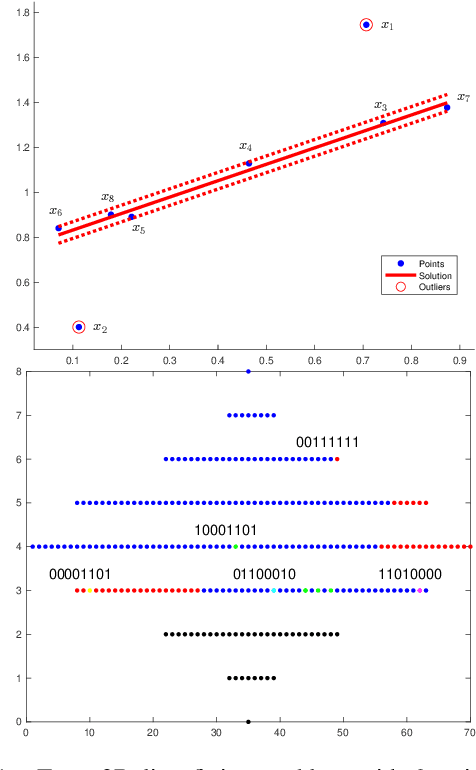
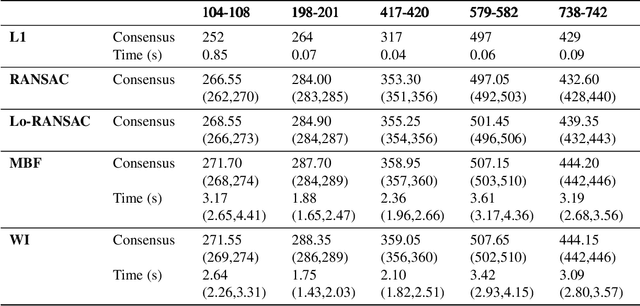
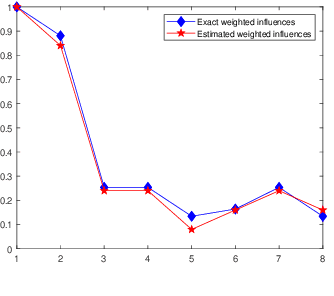
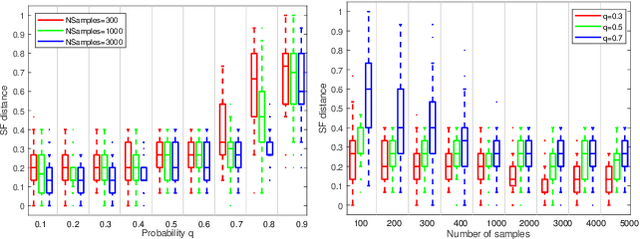
Robust model fitting is a fundamental problem in computer vision: used to pre-process raw data in the presence of outliers. Maximisation of Consensus (MaxCon) is one of the most popular robust criteria and widely used. Recently (Tennakoon et al. CVPR2021), a connection has been made between MaxCon and estimation of influences of a Monotone Boolean function. Equipping the Boolean cube with different measures and adopting different sampling strategies (two sides of the same coin) can have differing effects: which leads to the current study. This paper studies the concept of weighted influences for solving MaxCon. In particular, we study endowing the Boolean cube with the Bernoulli measure and performing biased (as opposed to uniform) sampling. Theoretically, we prove the weighted influences, under this measure, of points belonging to larger structures are smaller than those of points belonging to smaller structures in general. We also consider another "natural" family of sampling/weighting strategies, sampling with uniform measure concentrated on a particular (Hamming) level of the cube. Based on weighted sampling, we modify the algorithm of Tennakoon et al., and test on both synthetic and real datasets. This paper is not promoting a new approach per se, but rather studying the issue of weighted sampling. Accordingly, we are not claiming to have produced a superior algorithm: rather we show some modest gains of Bernoulli sampling, and we illuminate some of the interactions between structure in data and weighted sampling.

Consensus Maximisation Using Influences of Monotone Boolean Functions

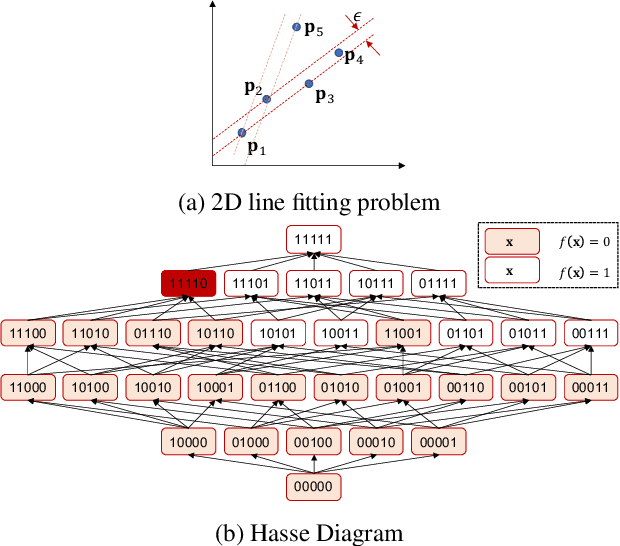
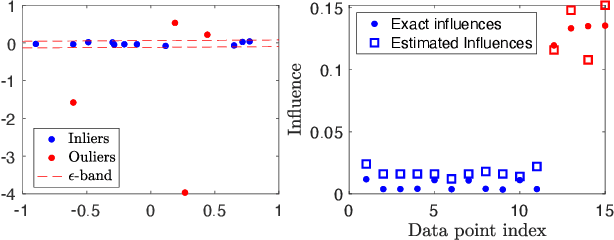
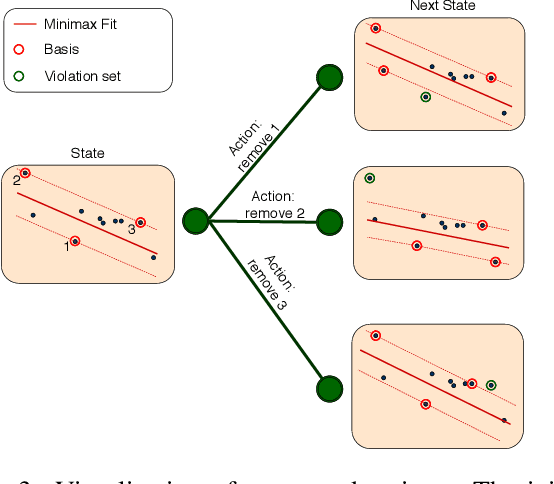
Consensus maximisation (MaxCon), which is widely used for robust fitting in computer vision, aims to find the largest subset of data that fits the model within some tolerance level. In this paper, we outline the connection between MaxCon problem and the abstract problem of finding the maximum upper zero of a Monotone Boolean Function (MBF) defined over the Boolean Cube. Then, we link the concept of influences (in a MBF) to the concept of outlier (in MaxCon) and show that influences of points belonging to the largest structure in data would generally be smaller under certain conditions. Based on this observation, we present an iterative algorithm to perform consensus maximisation. Results for both synthetic and real visual data experiments show that the MBF based algorithm is capable of generating a near optimal solution relatively quickly. This is particularly important where there are large number of outliers (gross or pseudo) in the observed data.

Unsupervised Learning for Robust Fitting:A Reinforcement Learning Approach

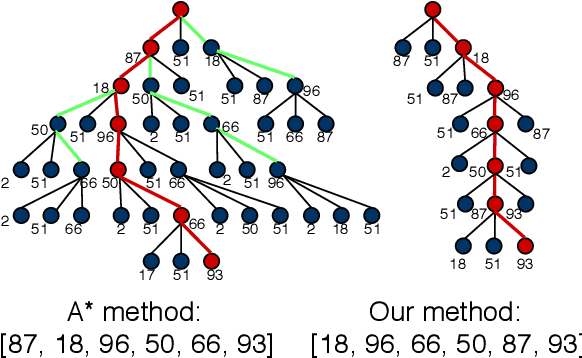
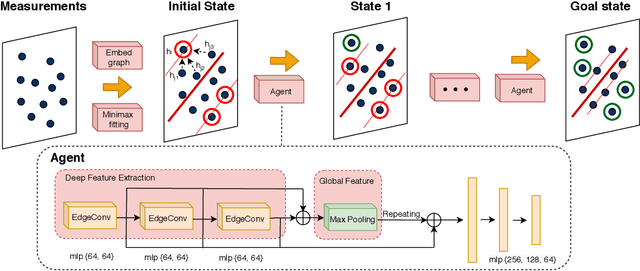
Robust model fitting is a core algorithm in a large number of computer vision applications. Solving this problem efficiently for datasets highly contaminated with outliers is, however, still challenging due to the underlying computational complexity. Recent literature has focused on learning-based algorithms. However, most approaches are supervised which require a large amount of labelled training data. In this paper, we introduce a novel unsupervised learning framework that learns to directly solve robust model fitting. Unlike other methods, our work is agnostic to the underlying input features, and can be easily generalized to a wide variety of LP-type problems with quasi-convex residuals. We empirically show that our method outperforms existing unsupervised learning approaches, and achieves competitive results compared to traditional methods on several important computer vision problems.

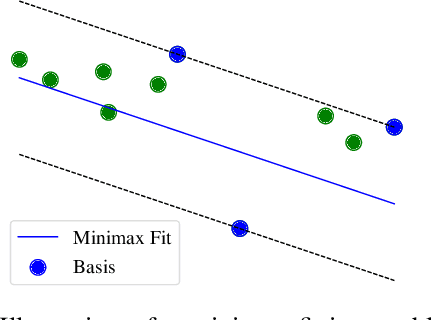
Monotone Boolean Functions, Feasibility/Infeasibility, LP-type problems and MaxCon

This paper outlines connections between Monotone Boolean Functions, LP-Type problems and the Maximum Consensus Problem. The latter refers to a particular type of robust fitting characterisation, popular in Computer Vision (MaxCon). Indeed, this is our main motivation but we believe the results of the study of these connections are more widely applicable to LP-type problems (at least 'thresholded versions', as we describe), and perhaps even more widely. We illustrate, with examples from Computer Vision, how the resulting perspectives suggest new algorithms. Indeed, we focus, in the experimental part, on how the Influence (a property of Boolean Functions that takes on a special form if the function is Monotone) can guide a search for the MaxCon solution.