Consensus Maximisation Using Influences of Monotone Boolean Functions
Paper and Code
Mar 06, 2021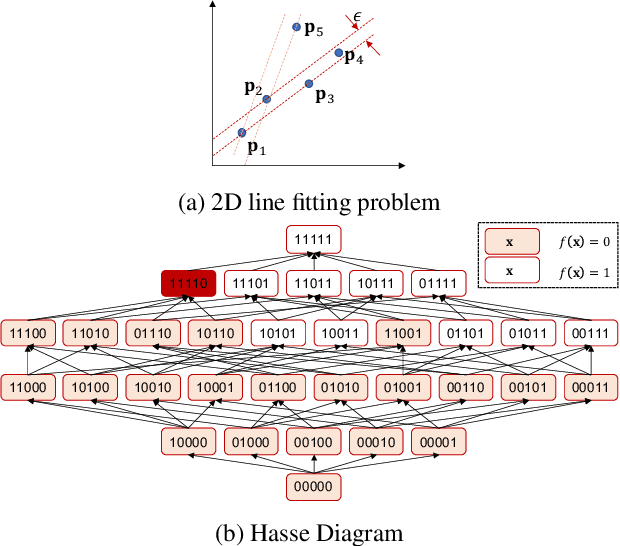

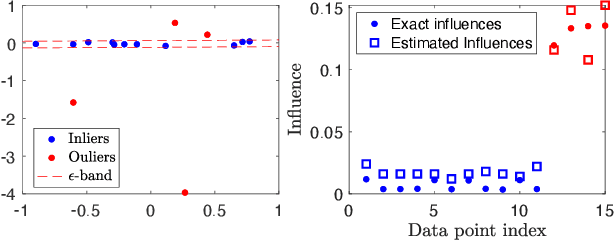

Consensus maximisation (MaxCon), which is widely used for robust fitting in computer vision, aims to find the largest subset of data that fits the model within some tolerance level. In this paper, we outline the connection between MaxCon problem and the abstract problem of finding the maximum upper zero of a Monotone Boolean Function (MBF) defined over the Boolean Cube. Then, we link the concept of influences (in a MBF) to the concept of outlier (in MaxCon) and show that influences of points belonging to the largest structure in data would generally be smaller under certain conditions. Based on this observation, we present an iterative algorithm to perform consensus maximisation. Results for both synthetic and real visual data experiments show that the MBF based algorithm is capable of generating a near optimal solution relatively quickly. This is particularly important where there are large number of outliers (gross or pseudo) in the observed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge