Multilingual and Explainable Text Detoxification with Parallel Corpora

Even with various regulations in place across countries and social media platforms (Government of India, 2021; European Parliament and Council of the European Union, 2022, digital abusive speech remains a significant issue. One potential approach to address this challenge is automatic text detoxification, a text style transfer (TST) approach that transforms toxic language into a more neutral or non-toxic form. To date, the availability of parallel corpora for the text detoxification task (Logachevavet al., 2022; Atwell et al., 2022; Dementievavet al., 2024a) has proven to be crucial for state-of-the-art approaches. With this work, we extend parallel text detoxification corpus to new languages -- German, Chinese, Arabic, Hindi, and Amharic -- testing in the extensive multilingual setup TST baselines. Next, we conduct the first of its kind an automated, explainable analysis of the descriptive features of both toxic and non-toxic sentences, diving deeply into the nuances, similarities, and differences of toxicity and detoxification across 9 languages. Finally, based on the obtained insights, we experiment with a novel text detoxification method inspired by the Chain-of-Thoughts reasoning approach, enhancing the prompting process through clustering on relevant descriptive attributes.

Explainable AI Approach using Near Misses Analysis

This paper introduces a novel XAI approach based on near-misses analysis (NMA). This approach reveals a hierarchy of logical 'concepts' inferred from the latent decision-making process of a Neural Network (NN) without delving into its explicit structure. We examined our proposed XAI approach on different network architectures that vary in size and shape (e.g., ResNet, VGG, EfficientNet, MobileNet) on several datasets (ImageNet and CIFAR100). The results demonstrate its usability to reflect NNs latent process of concepts generation. We generated a new metric for explainability. Moreover, our experiments suggest that efficient architectures, which achieve a similar accuracy level with much less neurons may still pay the price of explainability and robustness in terms of concepts generation. We, thus, pave a promising new path for XAI research to follow.

Using Deepfake Technologies for Word Emphasis Detection

In this work, we consider the task of automated emphasis detection for spoken language. This problem is challenging in that emphasis is affected by the particularities of speech of the subject, for example the subject accent, dialect or voice. To address this task, we propose to utilize deep fake technology to produce an emphasis devoid speech for this speaker. This requires extracting the text of the spoken voice, and then using a voice sample from the same speaker to produce emphasis devoid speech for this task. By comparing the generated speech with the spoken voice, we are able to isolate patterns of emphasis which are relatively easy to detect.

Anomaly Detection for Fraud in Cryptocurrency Time Series

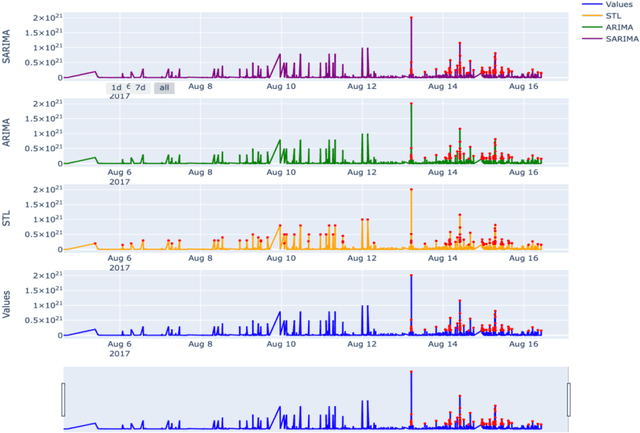
Since the inception of Bitcoin in 2009, the market of cryptocurrencies has grown beyond initial expectations as daily trades exceed $10 billion. As industries become automated, the need for an automated fraud detector becomes very apparent. Detecting anomalies in real time prevents potential accidents and economic losses. Anomaly detection in multivariate time series data poses a particular challenge because it requires simultaneous consideration of temporal dependencies and relationships between variables. Identifying an anomaly in real time is not an easy task specifically because of the exact anomalistic behavior they observe. Some points may present pointwise global or local anomalistic behavior, while others may be anomalistic due to their frequency or seasonal behavior or due to a change in the trend. In this paper we suggested working on real time series of trades of Ethereum from specific accounts and surveyed a large variety of different algorithms traditional and new. We categorized them according to the strategy and the anomalistic behavior which they search and showed that when bundling them together to different groups, they can prove to be a good real-time detector with an alarm time of no longer than a few seconds and with very high confidence.

Nested Barycentric Coordinate System as an Explicit Feature Map

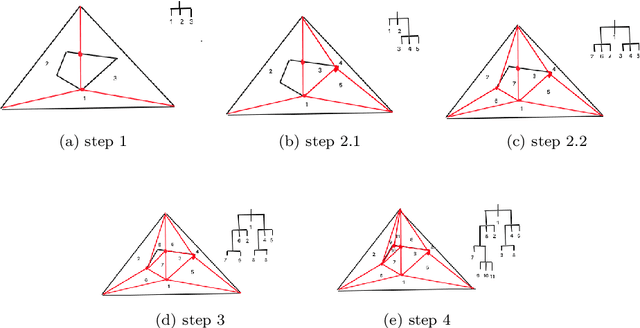
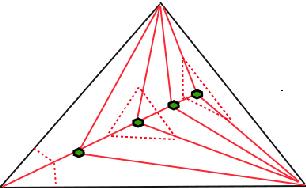
We propose a new embedding method which is particularly well-suited for settings where the sample size greatly exceeds the ambient dimension. Our technique consists of partitioning the space into simplices and then embedding the data points into features corresponding to the simplices' barycentric coordinates. We then train a linear classifier in the rich feature space obtained from the simplices. The decision boundary may be highly non-linear, though it is linear within each simplex (and hence piecewise-linear overall). Further, our method can approximate any convex body. We give generalization bounds based on empirical margin and a novel hybrid sample compression technique. An extensive empirical evaluation shows that our method consistently outperforms a range of popular kernel embedding methods.

Apportioned Margin Approach for Cost Sensitive Large Margin Classifiers

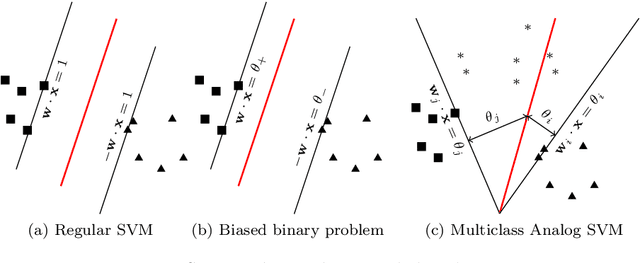
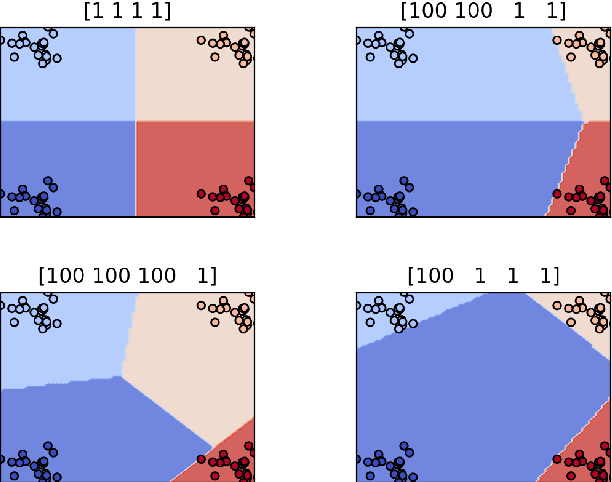
We consider the problem of cost sensitive multiclass classification, where we would like to increase the sensitivity of an important class at the expense of a less important one. We adopt an {\em apportioned margin} framework to address this problem, which enables an efficient margin shift between classes that share the same boundary. The decision boundary between all pairs of classes divides the margin between them in accordance to a given prioritization vector, which yields a tighter error bound for the important classes while also reducing the overall out-of-sample error. In addition to demonstrating an efficient implementation of our framework, we derive generalization bounds, demonstrate Fisher consistency, adapt the framework to Mercer's kernel and to neural networks, and report promising empirical results on all accounts.

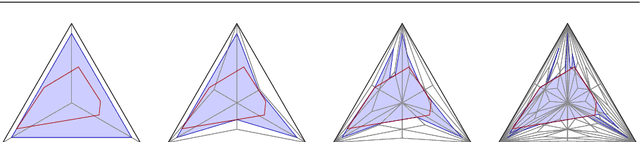
Learning convex polytopes with margin

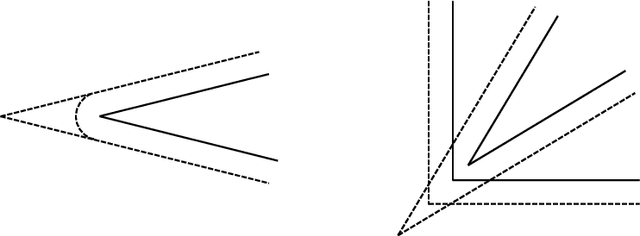
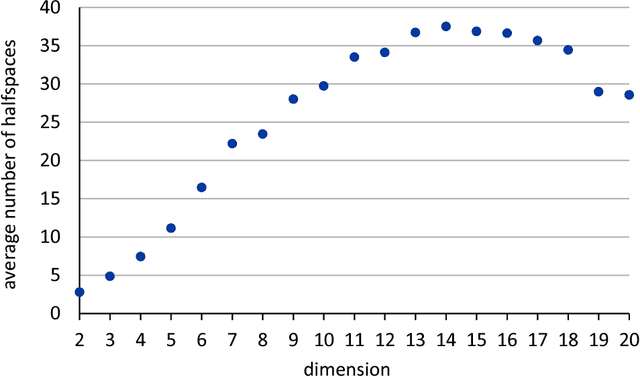
We present a near-optimal algorithm for properly learning convex polytopes in the realizable PAC setting from data with a margin. Our first contribution is to identify distinct generalizations of the notion of {\em margin} from hyperplanes to polytopes and to understand how they relate geometrically; this result may be of interest beyond the learning setting. Our novel learning algorithm constructs a consistent polytope as an intersection of about $t \log t$ halfspaces in time polynomial in $t$ (where $t$ is the number of halfspaces forming an optimal polytope). This is an exponential improvement over the state of the art [Arriaga and Vempala, 2006]. We also improve over the super-polynomial-in-$t$ algorithm of Klivans and Servedio [2008], while achieving a better sample complexity. Finally, we provide the first nearly matching hardness-of-approximation lower bound, whence our claim of near optimality.