Weighted Distance Nearest Neighbor Condensing

The problem of nearest neighbor condensing has enjoyed a long history of study, both in its theoretical and practical aspects. In this paper, we introduce the problem of weighted distance nearest neighbor condensing, where one assigns weights to each point of the condensed set, and then new points are labeled based on their weighted distance nearest neighbor in the condensed set. We study the theoretical properties of this new model, and show that it can produce dramatically better condensing than the standard nearest neighbor rule, yet is characterized by generalization bounds almost identical to the latter. We then suggest a condensing heuristic for our new problem. We demonstrate Bayes consistency for this heuristic, and also show promising empirical results.

Using Deepfake Technologies for Word Emphasis Detection

In this work, we consider the task of automated emphasis detection for spoken language. This problem is challenging in that emphasis is affected by the particularities of speech of the subject, for example the subject accent, dialect or voice. To address this task, we propose to utilize deep fake technology to produce an emphasis devoid speech for this speaker. This requires extracting the text of the spoken voice, and then using a voice sample from the same speaker to produce emphasis devoid speech for this task. By comparing the generated speech with the spoken voice, we are able to isolate patterns of emphasis which are relatively easy to detect.

Functions with average smoothness: structure, algorithms, and learning

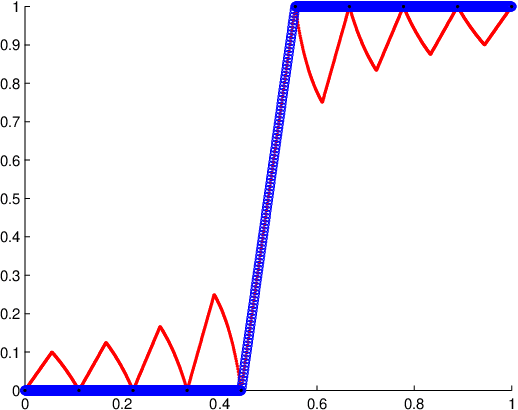
We initiate a program of average-smoothness analysis for efficiently learning real-valued functions on metric spaces. Rather than using the (global) Lipschitz constant as the regularizer, we define a local slope at each point and gauge the function complexity as the average of these values. Since the average is often much smaller than the maximum, this complexity measure can yield considerably sharper generalization bounds --- assuming that these admit a refinement where the global Lipschitz constant is replaced by our average of local slopes. Our first major contribution is to obtain just such distribution-sensitive bounds. This required overcoming a number of technical challenges, perhaps the most significant of which was bounding the {\em empirical} covering numbers, which can be much worse-behaved than the ambient ones. This in turn is based on a novel Lipschitz-type extension, which is a pointwise minimizer of the local slope, and may be of independent interest. Our combinatorial results are accompanied by efficient algorithms for denoising the random sample, as well as guarantees that the extension from the sample to the whole space will continue to be, with high probability, smooth on average. Along the way we discover a surprisingly rich combinatorial and analytic structure in the function class we define.

Nested Barycentric Coordinate System as an Explicit Feature Map

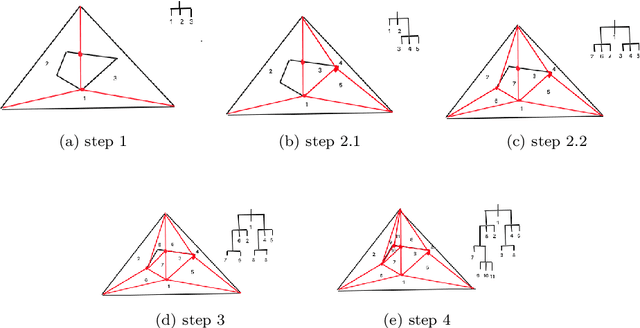
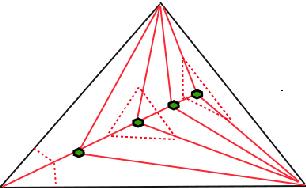
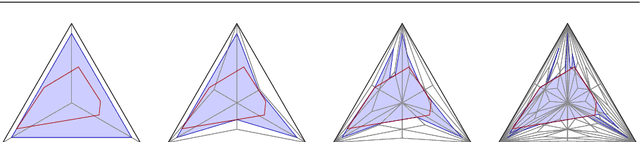
We propose a new embedding method which is particularly well-suited for settings where the sample size greatly exceeds the ambient dimension. Our technique consists of partitioning the space into simplices and then embedding the data points into features corresponding to the simplices' barycentric coordinates. We then train a linear classifier in the rich feature space obtained from the simplices. The decision boundary may be highly non-linear, though it is linear within each simplex (and hence piecewise-linear overall). Further, our method can approximate any convex body. We give generalization bounds based on empirical margin and a novel hybrid sample compression technique. An extensive empirical evaluation shows that our method consistently outperforms a range of popular kernel embedding methods.

Apportioned Margin Approach for Cost Sensitive Large Margin Classifiers

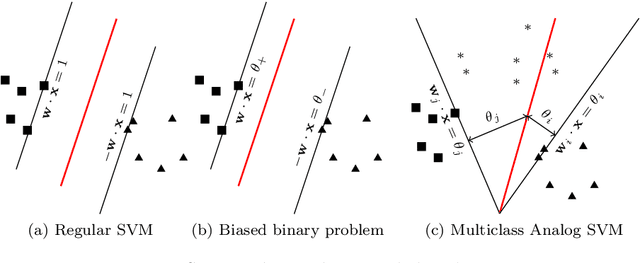
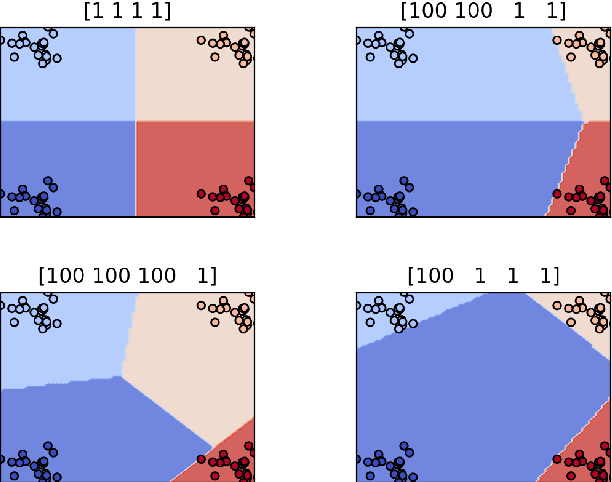
We consider the problem of cost sensitive multiclass classification, where we would like to increase the sensitivity of an important class at the expense of a less important one. We adopt an {\em apportioned margin} framework to address this problem, which enables an efficient margin shift between classes that share the same boundary. The decision boundary between all pairs of classes divides the margin between them in accordance to a given prioritization vector, which yields a tighter error bound for the important classes while also reducing the overall out-of-sample error. In addition to demonstrating an efficient implementation of our framework, we derive generalization bounds, demonstrate Fisher consistency, adapt the framework to Mercer's kernel and to neural networks, and report promising empirical results on all accounts.

Classification in asymmetric spaces via sample compression

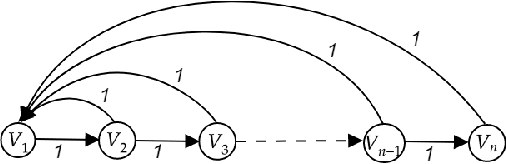
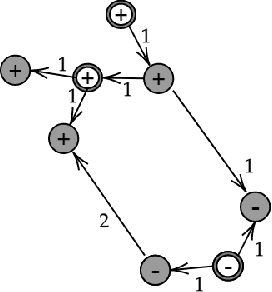
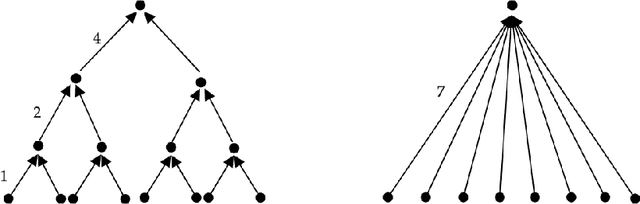
We initiate the rigorous study of classification in quasi-metric spaces. These are point sets endowed with a distance function that is non-negative and also satisfies the triangle inequality, but is asymmetric. We develop and refine a learning algorithm for quasi-metrics based on sample compression and nearest neighbor, and prove that it has favorable statistical properties.

Learning convex polytopes with margin

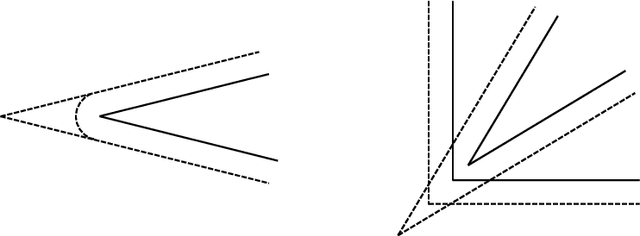
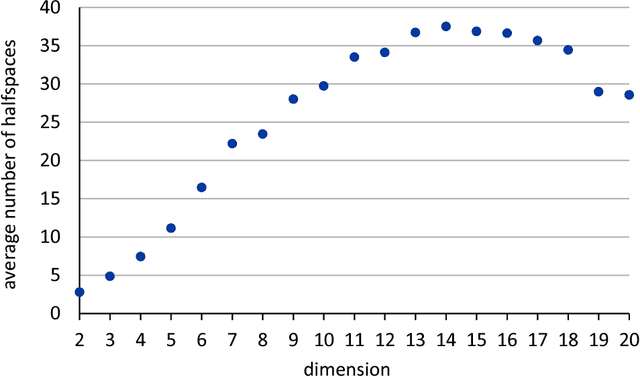
We present a near-optimal algorithm for properly learning convex polytopes in the realizable PAC setting from data with a margin. Our first contribution is to identify distinct generalizations of the notion of {\em margin} from hyperplanes to polytopes and to understand how they relate geometrically; this result may be of interest beyond the learning setting. Our novel learning algorithm constructs a consistent polytope as an intersection of about $t \log t$ halfspaces in time polynomial in $t$ (where $t$ is the number of halfspaces forming an optimal polytope). This is an exponential improvement over the state of the art [Arriaga and Vempala, 2006]. We also improve over the super-polynomial-in-$t$ algorithm of Klivans and Servedio [2008], while achieving a better sample complexity. Finally, we provide the first nearly matching hardness-of-approximation lower bound, whence our claim of near optimality.

Near-optimal sample compression for nearest neighbors

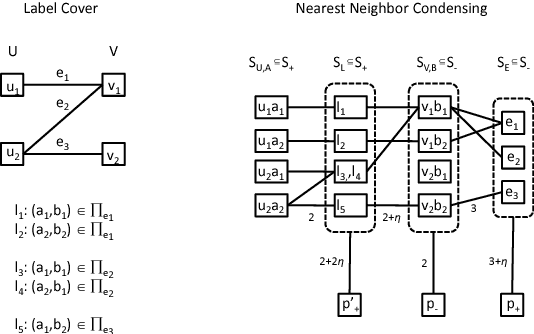
We present the first sample compression algorithm for nearest neighbors with non-trivial performance guarantees. We complement these guarantees by demonstrating almost matching hardness lower bounds, which show that our bound is nearly optimal. Our result yields new insight into margin-based nearest neighbor classification in metric spaces and allows us to significantly sharpen and simplify existing bounds. Some encouraging empirical results are also presented.

Efficient Regression in Metric Spaces via Approximate Lipschitz Extension

We present a framework for performing efficient regression in general metric spaces. Roughly speaking, our regressor predicts the value at a new point by computing a Lipschitz extension --- the smoothest function consistent with the observed data --- after performing structural risk minimization to avoid overfitting. We obtain finite-sample risk bounds with minimal structural and noise assumptions, and a natural speed-precision tradeoff. The offline (learning) and online (prediction) stages can be solved by convex programming, but this naive approach has runtime complexity $O(n^3)$, which is prohibitive for large datasets. We design instead a regression algorithm whose speed and generalization performance depend on the intrinsic dimension of the data, to which the algorithm adapts. While our main innovation is algorithmic, the statistical results may also be of independent interest.

Adaptive Metric Dimensionality Reduction

We study adaptive data-dependent dimensionality reduction in the context of supervised learning in general metric spaces. Our main statistical contribution is a generalization bound for Lipschitz functions in metric spaces that are doubling, or nearly doubling. On the algorithmic front, we describe an analogue of PCA for metric spaces: namely an efficient procedure that approximates the data's intrinsic dimension, which is often much lower than the ambient dimension. Our approach thus leverages the dual benefits of low dimensionality: (1) more efficient algorithms, e.g., for proximity search, and (2) more optimistic generalization bounds.