Nested Barycentric Coordinate System as an Explicit Feature Map
Paper and Code
Feb 05, 2020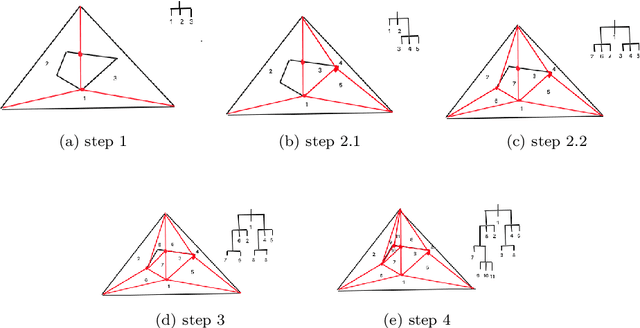

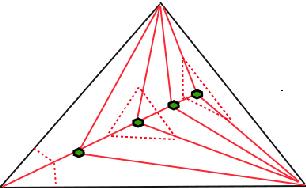
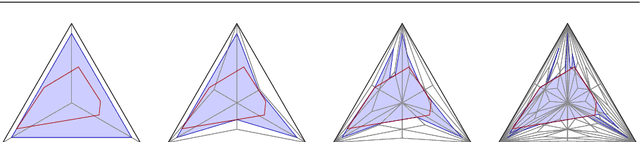
We propose a new embedding method which is particularly well-suited for settings where the sample size greatly exceeds the ambient dimension. Our technique consists of partitioning the space into simplices and then embedding the data points into features corresponding to the simplices' barycentric coordinates. We then train a linear classifier in the rich feature space obtained from the simplices. The decision boundary may be highly non-linear, though it is linear within each simplex (and hence piecewise-linear overall). Further, our method can approximate any convex body. We give generalization bounds based on empirical margin and a novel hybrid sample compression technique. An extensive empirical evaluation shows that our method consistently outperforms a range of popular kernel embedding methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge