Gabriel Nivasch
Nested Barycentric Coordinate System as an Explicit Feature Map
Feb 05, 2020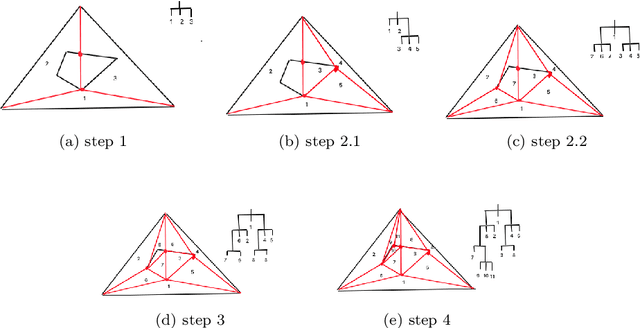

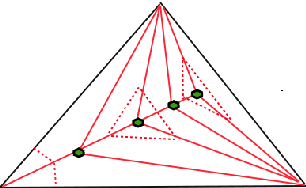
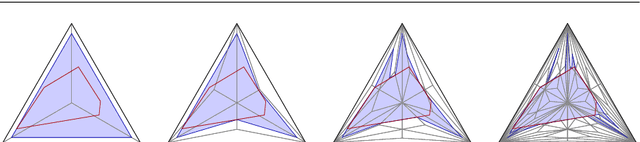
Abstract:We propose a new embedding method which is particularly well-suited for settings where the sample size greatly exceeds the ambient dimension. Our technique consists of partitioning the space into simplices and then embedding the data points into features corresponding to the simplices' barycentric coordinates. We then train a linear classifier in the rich feature space obtained from the simplices. The decision boundary may be highly non-linear, though it is linear within each simplex (and hence piecewise-linear overall). Further, our method can approximate any convex body. We give generalization bounds based on empirical margin and a novel hybrid sample compression technique. An extensive empirical evaluation shows that our method consistently outperforms a range of popular kernel embedding methods.
Learning convex polytopes with margin
May 24, 2018
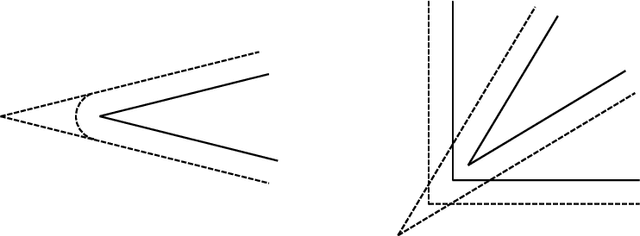
Abstract:We present a near-optimal algorithm for properly learning convex polytopes in the realizable PAC setting from data with a margin. Our first contribution is to identify distinct generalizations of the notion of {\em margin} from hyperplanes to polytopes and to understand how they relate geometrically; this result may be of interest beyond the learning setting. Our novel learning algorithm constructs a consistent polytope as an intersection of about $t \log t$ halfspaces in time polynomial in $t$ (where $t$ is the number of halfspaces forming an optimal polytope). This is an exponential improvement over the state of the art [Arriaga and Vempala, 2006]. We also improve over the super-polynomial-in-$t$ algorithm of Klivans and Servedio [2008], while achieving a better sample complexity. Finally, we provide the first nearly matching hardness-of-approximation lower bound, whence our claim of near optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge