Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Shira Ozeri
Classification in asymmetric spaces via sample compression
Sep 22, 2019Figures and Tables:
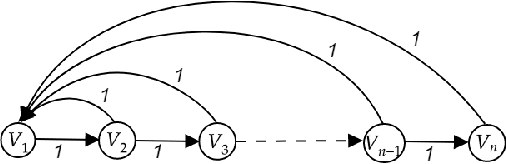
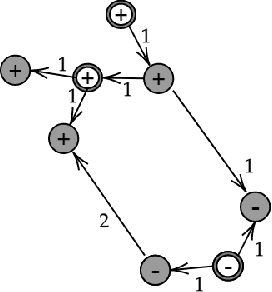
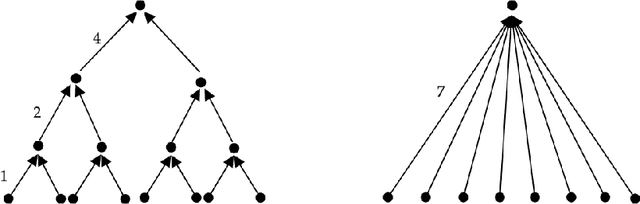




Abstract:We initiate the rigorous study of classification in quasi-metric spaces. These are point sets endowed with a distance function that is non-negative and also satisfies the triangle inequality, but is asymmetric. We develop and refine a learning algorithm for quasi-metrics based on sample compression and nearest neighbor, and prove that it has favorable statistical properties.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge