The Uniformly Rotated Mondrian Kernel

First proposed by Rahimi and Recht, random features are used to decrease the computational cost of kernel machines in large-scale problems. The Mondrian kernel is one such example of a fast random feature approximation of the Laplace kernel, generated by a computationally efficient hierarchical random partition of the input space known as the Mondrian process. In this work, we study a variation of this random feature map by using uniformly randomly rotated Mondrian processes to approximate a kernel that is invariant under rotations. We obtain a closed-form expression for this isotropic kernel, as well as a uniform convergence rate of the uniformly rotated Mondrian kernel to this limit. To this end, we utilize techniques from the theory of stationary random tessellations in stochastic geometry and prove a new result on the geometry of the typical cell of the superposition of uniformly random rotations of Mondrian tessellations. Finally, we test the empirical performance of this random feature map on both synthetic and real-world datasets, demonstrating its improved performance over the Mondrian kernel on a debiased dataset.

The Star Geometry of Critic-Based Regularizer Learning

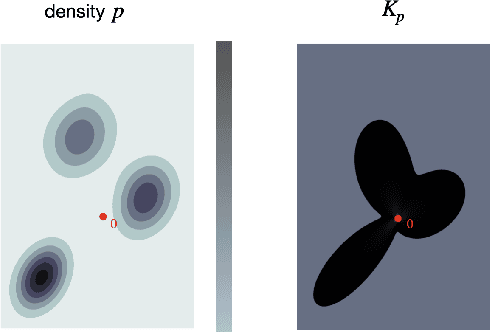
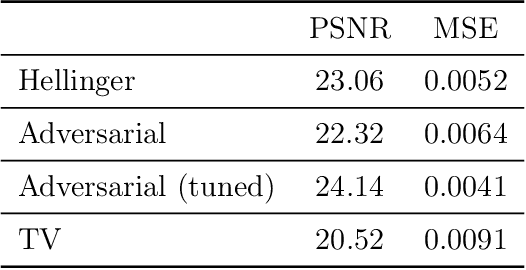
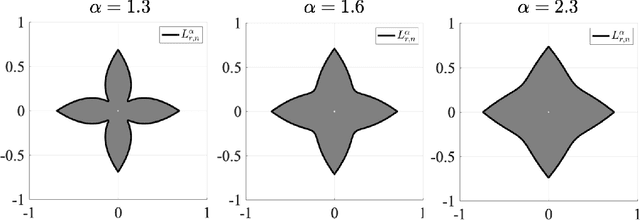
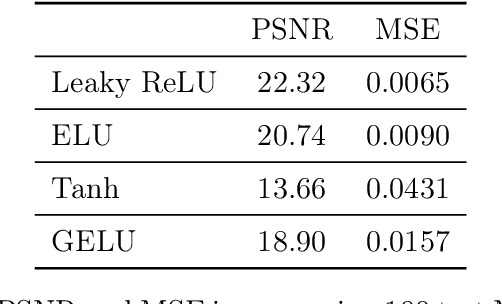
Variational regularization is a classical technique to solve statistical inference tasks and inverse problems, with modern data-driven approaches parameterizing regularizers via deep neural networks showcasing impressive empirical performance. Recent works along these lines learn task-dependent regularizers. This is done by integrating information about the measurements and ground-truth data in an unsupervised, critic-based loss function, where the regularizer attributes low values to likely data and high values to unlikely data. However, there is little theory about the structure of regularizers learned via this process and how it relates to the two data distributions. To make progress on this challenge, we initiate a study of optimizing critic-based loss functions to learn regularizers over a particular family of regularizers: gauges (or Minkowski functionals) of star-shaped bodies. This family contains regularizers that are commonly employed in practice and shares properties with regularizers parameterized by deep neural networks. We specifically investigate critic-based losses derived from variational representations of statistical distances between probability measures. By leveraging tools from star geometry and dual Brunn-Minkowski theory, we illustrate how these losses can be interpreted as dual mixed volumes that depend on the data distribution. This allows us to derive exact expressions for the optimal regularizer in certain cases. Finally, we identify which neural network architectures give rise to such star body gauges and when do such regularizers have favorable properties for optimization. More broadly, this work highlights how the tools of star geometry can aid in understanding the geometry of unsupervised regularizer learning.

TrIM: Transformed Iterative Mondrian Forests for Gradient-based Dimension Reduction and High-Dimensional Regression

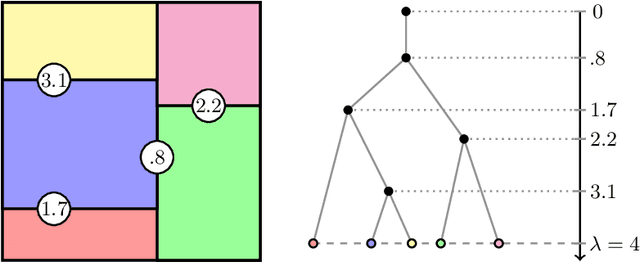
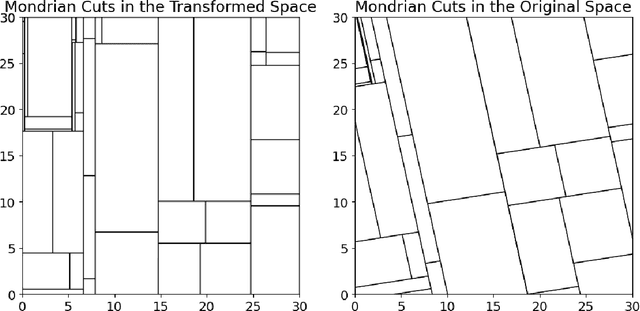
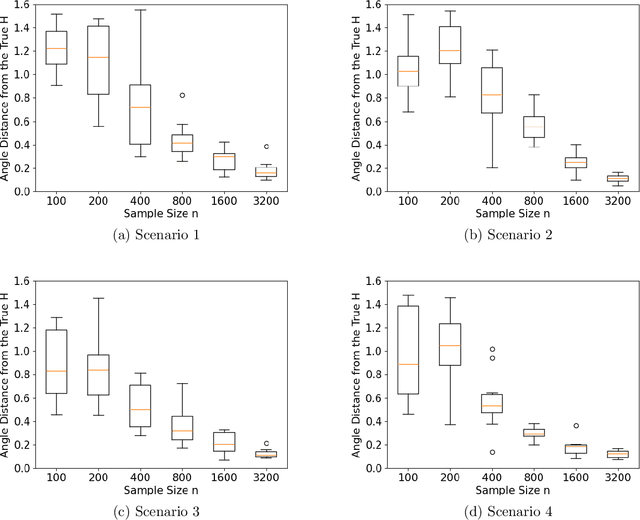
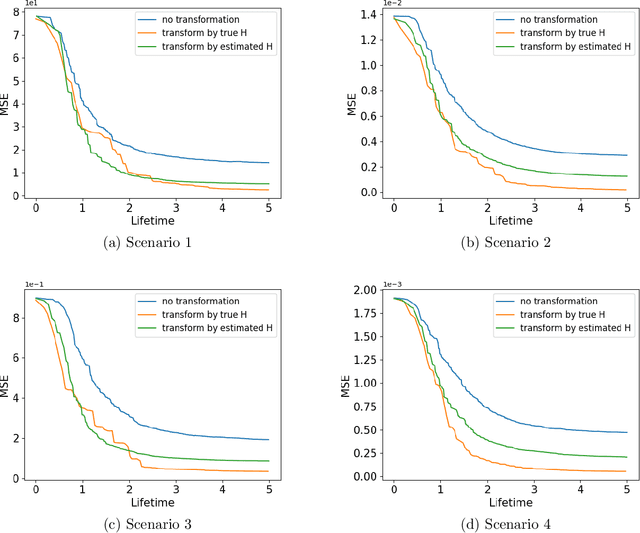
We propose a computationally efficient algorithm for gradient-based linear dimension reduction and high-dimensional regression. The algorithm initially computes a Mondrian forest and uses this estimator to identify a relevant feature subspace of the inputs from an estimate of the expected gradient outer product (EGOP) of the regression function. In addition, we introduce an iterative approach known as Transformed Iterative Mondrian (TrIM) forest to improve the Mondrian forest estimator by using the EGOP estimate to update the set of features and weights used by the Mondrian partitioning mechanism. We obtain consistency guarantees and convergence rates for the estimation of the EGOP matrix and the random forest estimator obtained from one iteration of the TrIM algorithm. Lastly, we demonstrate the effectiveness of our proposed algorithm for learning the relevant feature subspace across a variety of settings with both simulated and real data.

Statistical Advantages of Oblique Randomized Decision Trees and Forests

This work studies the statistical advantages of using features comprised of general linear combinations of covariates to partition the data in randomized decision tree and forest regression algorithms. Using random tessellation theory in stochastic geometry, we provide a theoretical analysis of a class of efficiently generated random tree and forest estimators that allow for oblique splits along such features. We call these estimators oblique Mondrian trees and forests, as the trees are generated by first selecting a set of features from linear combinations of the covariates and then running a Mondrian process that hierarchically partitions the data along these features. Generalization error bounds and convergence rates are obtained for the flexible dimension reduction model class of ridge functions (also known as multi-index models), where the output is assumed to depend on a low dimensional relevant feature subspace of the input domain. The results highlight how the risk of these estimators depends on the choice of features and quantify how robust the risk is with respect to error in the estimation of relevant features. The asymptotic analysis also provides conditions on the selected features along which the data is split for these estimators to obtain minimax optimal rates of convergence with respect to the dimension of the relevant feature subspace. Additionally, a lower bound on the risk of axis-aligned Mondrian trees (where features are restricted to the set of covariates) is obtained proving that these estimators are suboptimal for these linear dimension reduction models in general, no matter how the distribution over the covariates used to divide the data at each tree node is weighted.

Optimal Convex and Nonconvex Regularizers for a Data Source

In optimization-based approaches to inverse problems and to statistical estimation, it is common to augment the objective with a regularizer to address challenges associated with ill-posedness. The choice of a suitable regularizer is typically driven by prior domain information and computational considerations. Convex regularizers are attractive as they are endowed with certificates of optimality as well as the toolkit of convex analysis, but exhibit a computational scaling that makes them ill-suited beyond moderate-sized problem instances. On the other hand, nonconvex regularizers can often be deployed at scale, but do not enjoy the certification properties associated with convex regularizers. In this paper, we seek a systematic understanding of the power and the limitations of convex regularization by investigating the following questions: Given a distribution, what are the optimal regularizers, both convex and nonconvex, for data drawn from the distribution? What properties of a data source govern whether it is amenable to convex regularization? We address these questions for the class of continuous and positively homogenous regularizers for which convex and nonconvex regularizers correspond, respectively, to convex bodies and star bodies. By leveraging dual Brunn-Minkowski theory, we show that a radial function derived from a data distribution is the key quantity for identifying optimal regularizers and for assessing the amenability of a data source to convex regularization. Using tools such as $\Gamma$-convergence, we show that our results are robust in the sense that the optimal regularizers for a sample drawn from a distribution converge to their population counterparts as the sample size grows large. Finally, we give generalization guarantees that recover previous results for polyhedral regularizers (i.e., dictionary learning) and lead to new ones for semidefinite regularizers.

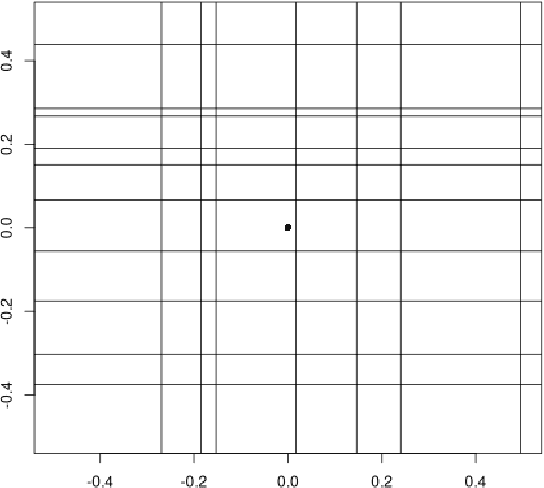
Spectrahedral Regression

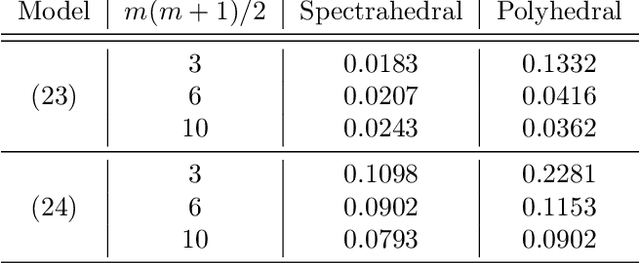
Convex regression is the problem of fitting a convex function to a data set consisting of input-output pairs. We present a new approach to this problem called spectrahedral regression, in which we fit a spectrahedral function to the data, i.e. a function that is the maximum eigenvalue of an affine matrix expression of the input. This method represents a significant generalization of polyhedral (also called max-affine) regression, in which a polyhedral function (a maximum of a fixed number of affine functions) is fit to the data. We prove bounds on how well spectrahedral functions can approximate arbitrary convex functions via statistical risk analysis. We also analyze an alternating minimization algorithm for the non-convex optimization problem of fitting the best spectrahedral function to a given data set. We show that this algorithm converges geometrically with high probability to a small ball around the optimal parameter given a good initialization. Finally, we demonstrate the utility of our approach with experiments on synthetic data sets as well as real data arising in applications such as economics and engineering design.

Minimax Rates for STIT and Poisson Hyperplane Random Forests

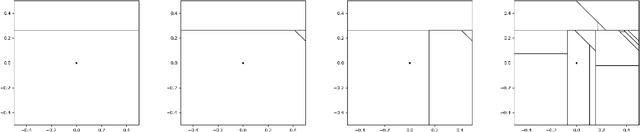
In [12], Mourtada, Ga\"{i}ffas and Scornet showed that, under proper tuning of the complexity parameters, random trees and forests built from the Mondrian process in $\mathbb{R}^d$ achieve the minimax rate for $\beta$-H\"{o}lder continuous functions, and random forests achieve the minimax rate for $(1+\beta)$-H\"{o}lder functions in arbitrary dimension, where $\beta \in (0,1]$. In this work, we show that a much larger class of random forests built from random partitions of $\mathbb{R}^d$ also achieve these minimax rates. This class includes STIT random forests, the most general class of random forests built from a self-similar and stationary partition of $\mathbb{R}^d$ by hyperplane cuts possible, as well as forests derived from Poisson hyperplane tessellations. Our proof technique relies on classical results as well as recent advances on stationary random tessellations in stochastic geometry.

Stochastic geometry to generalize the Mondrian Process

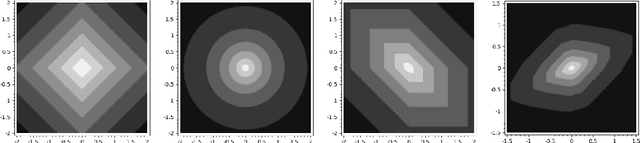
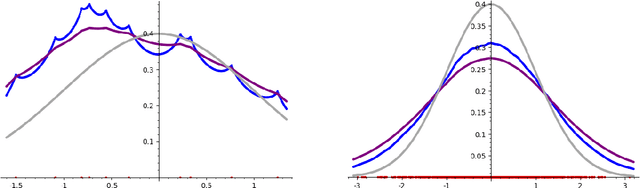
The Mondrian process is a stochastic process that produces a recursive partition of space with random axis-aligned cuts. Random forests and Laplace kernel approximations built from the Mondrian process have led to efficient online learning methods and Bayesian optimization. By viewing the Mondrian process as a special case of the stable under iterated tessellation (STIT) process, we utilize tools from stochastic geometry to resolve three fundamental questions concern generalizability of the Mondrian process in machine learning. First, we show that the Mondrian process with general cut directions can be efficiently simulated, but it is unlikely to give rise to better classification or regression algorithms. Second, we characterize all possible kernels that generalizations of the Mondrian process can approximate. This includes, for instance, various forms of the weighted Laplace kernel and the exponential kernel. Third, we give an explicit formula for the density estimator arising from a Mondrian forest. This allows for precise comparisons between the Mondrian forest, the Mondrian kernel and the Laplace kernel in density estimation. Our paper calls for further developments at the novel intersection of stochastic geometry and machine learning.