TrIM: Transformed Iterative Mondrian Forests for Gradient-based Dimension Reduction and High-Dimensional Regression
Paper and Code
Jul 13, 2024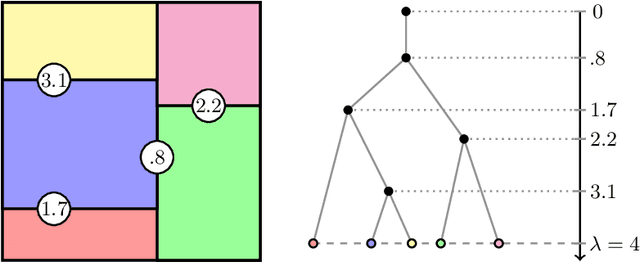
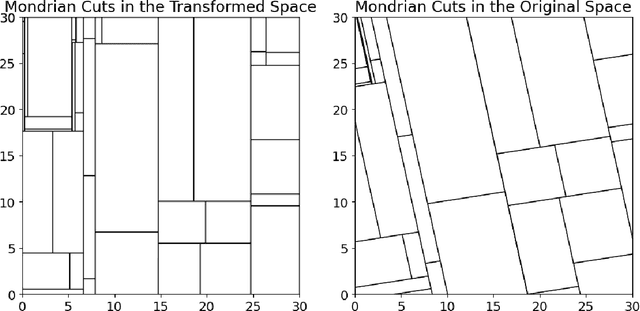
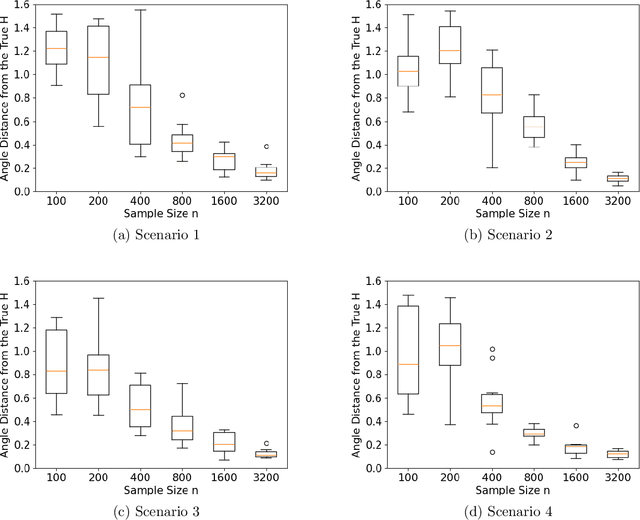
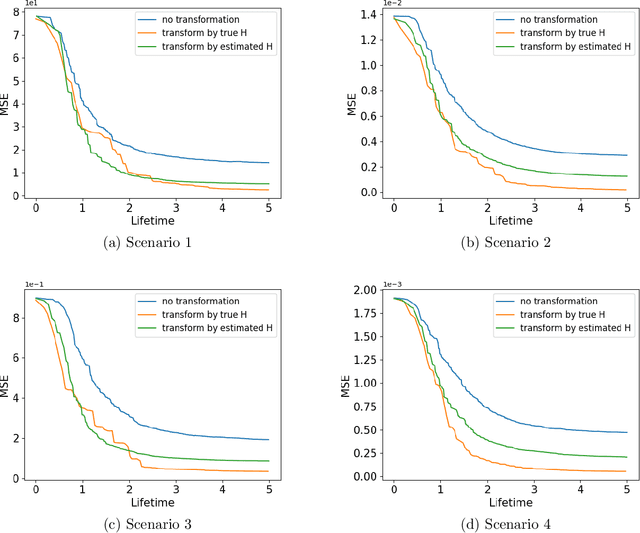
We propose a computationally efficient algorithm for gradient-based linear dimension reduction and high-dimensional regression. The algorithm initially computes a Mondrian forest and uses this estimator to identify a relevant feature subspace of the inputs from an estimate of the expected gradient outer product (EGOP) of the regression function. In addition, we introduce an iterative approach known as Transformed Iterative Mondrian (TrIM) forest to improve the Mondrian forest estimator by using the EGOP estimate to update the set of features and weights used by the Mondrian partitioning mechanism. We obtain consistency guarantees and convergence rates for the estimation of the EGOP matrix and the random forest estimator obtained from one iteration of the TrIM algorithm. Lastly, we demonstrate the effectiveness of our proposed algorithm for learning the relevant feature subspace across a variety of settings with both simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge