Stochastic geometry to generalize the Mondrian Process

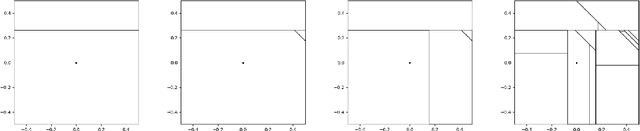
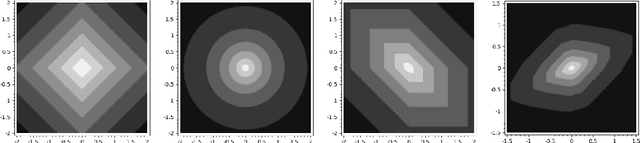
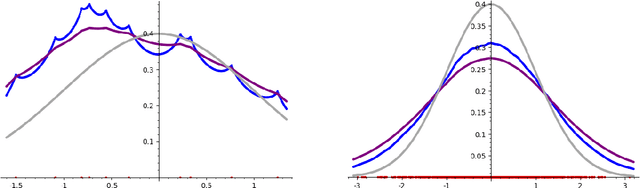
The Mondrian process is a stochastic process that produces a recursive partition of space with random axis-aligned cuts. Random forests and Laplace kernel approximations built from the Mondrian process have led to efficient online learning methods and Bayesian optimization. By viewing the Mondrian process as a special case of the stable under iterated tessellation (STIT) process, we utilize tools from stochastic geometry to resolve three fundamental questions concern generalizability of the Mondrian process in machine learning. First, we show that the Mondrian process with general cut directions can be efficiently simulated, but it is unlikely to give rise to better classification or regression algorithms. Second, we characterize all possible kernels that generalizations of the Mondrian process can approximate. This includes, for instance, various forms of the weighted Laplace kernel and the exponential kernel. Third, we give an explicit formula for the density estimator arising from a Mondrian forest. This allows for precise comparisons between the Mondrian forest, the Mondrian kernel and the Laplace kernel in density estimation. Our paper calls for further developments at the novel intersection of stochastic geometry and machine learning.