Single Point-Based Distributed Zeroth-Order Optimization with a Non-Convex Stochastic Objective Function

Zero-order (ZO) optimization is a powerful tool for dealing with realistic constraints. On the other hand, the gradient-tracking (GT) technique proved to be an efficient method for distributed optimization aiming to achieve consensus. However, it is a first-order (FO) method that requires knowledge of the gradient, which is not always possible in practice. In this work, we introduce a zero-order distributed optimization method based on a one-point estimate of the gradient tracking technique. We prove that this new technique converges with a single noisy function query at a time in the non-convex setting. We then establish a convergence rate of $O(\frac{1}{\sqrt[3]{K}})$ after a number of iterations K, which competes with that of $O(\frac{1}{\sqrt[4]{K}})$ of its centralized counterparts. Finally, a numerical example validates our theoretical results.

Communication and Energy Efficient Federated Learning using Zero-Order Optimization Technique

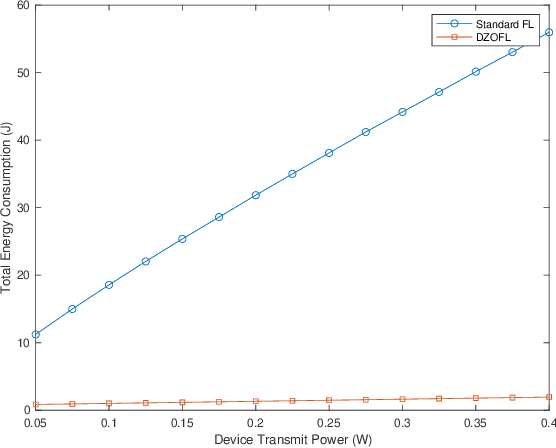
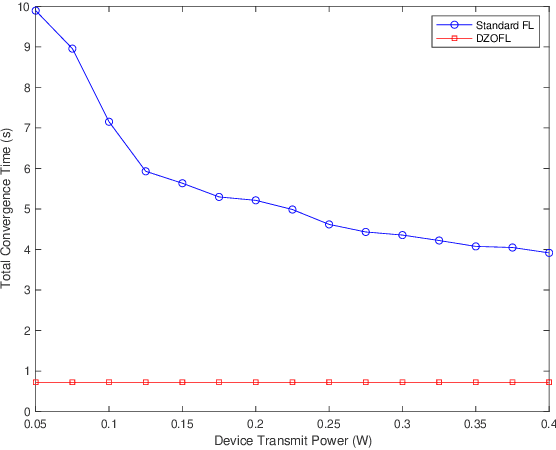
Federated learning (FL) is a popular machine learning technique that enables multiple users to collaboratively train a model while maintaining the user data privacy. A significant challenge in FL is the communication bottleneck in the upload direction, and thus the corresponding energy consumption of the devices, attributed to the increasing size of the model/gradient. In this paper, we address this issue by proposing a zero-order (ZO) optimization method that requires the upload of a quantized single scalar per iteration by each device instead of the whole gradient vector. We prove its theoretical convergence and find an upper bound on its convergence rate in the non-convex setting, and we discuss its implementation in practical scenarios. Our FL method and the corresponding convergence analysis take into account the impact of quantization and packet dropping due to wireless errors. We show also the superiority of our method, in terms of communication overhead and energy consumption, as compared to standard gradient-based FL methods.

Rendering Wireless Environments Useful for Gradient Estimators: A Zero-Order Stochastic Federated Learning Method

Federated learning (FL) is a novel approach to machine learning that allows multiple edge devices to collaboratively train a model without disclosing their raw data. However, several challenges hinder the practical implementation of this approach, especially when devices and the server communicate over wireless channels, as it suffers from communication and computation bottlenecks in this case. By utilizing a communication-efficient framework, we propose a novel zero-order (ZO) method with a one-point gradient estimator that harnesses the nature of the wireless communication channel without requiring the knowledge of the channel state coefficient. It is the first method that includes the wireless channel in the learning algorithm itself instead of wasting resources to analyze it and remove its impact. The two main difficulties of this work are that in FL, the objective function is usually not convex, which makes the extension of FL to ZO methods challenging, and that including the impact of wireless channels requires extra attention. However, we overcome these difficulties and comprehensively analyze the proposed zero-order federated learning (ZOFL) framework. We establish its convergence theoretically, and we prove a convergence rate of $O(\frac{1}{\sqrt[3]{K}})$ in the nonconvex setting. We further demonstrate the potential of our algorithm with experimental results, taking into account independent and identically distributed (IID) and non-IID device data distributions.

Zero-Order One-Point Estimate with Distributed Stochastic Gradient-Tracking Technique

In this work, we consider a distributed multi-agent stochastic optimization problem, where each agent holds a local objective function that is smooth and convex, and that is subject to a stochastic process. The goal is for all agents to collaborate to find a common solution that optimizes the sum of these local functions. With the practical assumption that agents can only obtain noisy numerical function queries at exactly one point at a time, we extend the distributed stochastic gradient-tracking method to the bandit setting where we don't have an estimate of the gradient, and we introduce a zero-order (ZO) one-point estimate (1P-DSGT). We analyze the convergence of this novel technique for smooth and convex objectives using stochastic approximation tools, and we prove that it converges almost surely to the optimum. We then study the convergence rate for when the objectives are additionally strongly convex. We obtain a rate of $O(\frac{1}{\sqrt{k}})$ after a sufficient number of iterations $k > K_2$ which is usually optimal for techniques utilizing one-point estimators. We also provide a regret bound of $O(\sqrt{k})$, which is exceptionally good compared to the aforementioned techniques. We further illustrate the usefulness of the proposed technique using numerical experiments.