EARL: Entropy-Aware RL Alignment of LLMs for Reliable RTL Code Generation

Recent advances in large language models (LLMs) have demonstrated significant potential in hardware design automation, particularly in using natural language to synthesize Register-Transfer Level (RTL) code. Despite this progress, a gap remains between model capability and the demands of real-world RTL design, including syntax errors, functional hallucinations, and weak alignment to designer intent. Reinforcement Learning with Verifiable Rewards (RLVR) offers a promising approach to bridge this gap, as hardware provides executable and formally checkable signals that can be used to further align model outputs with design intent. However, in long, structured RTL code sequences, not all tokens contribute equally to functional correctness, and naïvely spreading gradients across all tokens dilutes learning signals. A key insight from our entropy analysis in RTL generation is that only a small fraction of tokens (e.g., always, if, assign, posedge) exhibit high uncertainty and largely influence control flow and module structure. To address these challenges, we present EARL, an Entropy-Aware Reinforcement Learning framework for Verilog generation. EARL performs policy optimization using verifiable reward signals and introduces entropy-guided selective updates that gate policy gradients to high-entropy tokens. This approach preserves training stability and concentrates gradient updates on functionally important regions of code. Our experiments on VerilogEval and RTLLM show that EARL improves functional pass rates over prior LLM baselines by up to 14.7%, while reducing unnecessary updates and improving training stability. These results indicate that focusing RL on critical, high-uncertainty tokens enables more reliable and targeted policy improvement for structured RTL code generation.

Robust Reinforcement Learning on State Observations with Learned Optimal Adversary

We study the robustness of reinforcement learning (RL) with adversarially perturbed state observations, which aligns with the setting of many adversarial attacks to deep reinforcement learning (DRL) and is also important for rolling out real-world RL agent under unpredictable sensing noise. With a fixed agent policy, we demonstrate that an optimal adversary to perturb state observations can be found, which is guaranteed to obtain the worst case agent reward. For DRL settings, this leads to a novel empirical adversarial attack to RL agents via a learned adversary that is much stronger than previous ones. To enhance the robustness of an agent, we propose a framework of alternating training with learned adversaries (ATLA), which trains an adversary online together with the agent using policy gradient following the optimal adversarial attack framework. Additionally, inspired by the analysis of state-adversarial Markov decision process (SA-MDP), we show that past states and actions (history) can be useful for learning a robust agent, and we empirically find a LSTM based policy can be more robust under adversaries. Empirical evaluations on a few continuous control environments show that ATLA achieves state-of-the-art performance under strong adversaries. Our code is available at https://github.com/huanzhang12/ATLA_robust_RL.

On $\ell_p$-norm Robustness of Ensemble Stumps and Trees

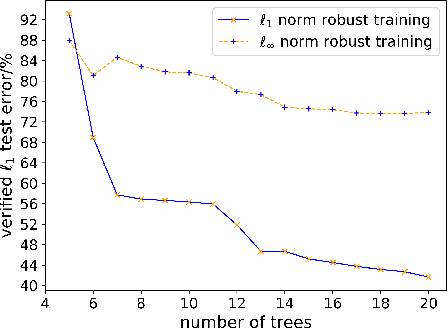
Recent papers have demonstrated that ensemble stumps and trees could be vulnerable to small input perturbations, so robustness verification and defense for those models have become an important research problem. However, due to the structure of decision trees, where each node makes decision purely based on one feature value, all the previous works only consider the $\ell_\infty$ norm perturbation. To study robustness with respect to a general $\ell_p$ norm perturbation, one has to consider the correlation between perturbations on different features, which has not been handled by previous algorithms. In this paper, we study the problem of robustness verification and certified defense with respect to general $\ell_p$ norm perturbations for ensemble decision stumps and trees. For robustness verification of ensemble stumps, we prove that complete verification is NP-complete for $p\in(0, \infty)$ while polynomial time algorithms exist for $p=0$ or $\infty$. For $p\in(0, \infty)$ we develop an efficient dynamic programming based algorithm for sound verification of ensemble stumps. For ensemble trees, we generalize the previous multi-level robustness verification algorithm to $\ell_p$ norm. We demonstrate the first certified defense method for training ensemble stumps and trees with respect to $\ell_p$ norm perturbations, and verify its effectiveness empirically on real datasets.

Multi-Stage Influence Function

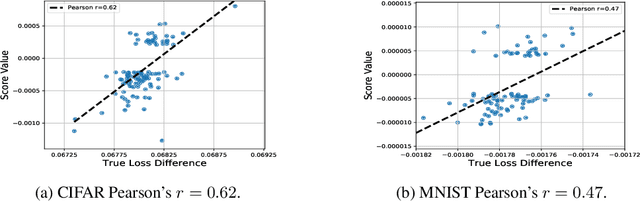
Multi-stage training and knowledge transfer, from a large-scale pretraining task to various finetuning tasks, have revolutionized natural language processing and computer vision resulting in state-of-the-art performance improvements. In this paper, we develop a multi-stage influence function score to track predictions from a finetuned model all the way back to the pretraining data. With this score, we can identify the pretraining examples in the pretraining task that contribute most to a prediction in the finetuning task. The proposed multi-stage influence function generalizes the original influence function for a single model in (Koh & Liang, 2017), thereby enabling influence computation through both pretrained and finetuned models. We study two different scenarios with the pretrained embeddings fixed or updated in the finetuning tasks. We test our proposed method in various experiments to show its effectiveness and potential applications.

Robust Deep Reinforcement Learning against Adversarial Perturbations on Observations

Deep Reinforcement Learning (DRL) is vulnerable to small adversarial perturbations on state observations. These perturbations do not alter the environment directly but can mislead the agent into making suboptimal decisions. We analyze the Markov Decision Process (MDP) under this threat model and utilize tools from the neural net-work verification literature to enable robust train-ing for DRL under observational perturbations. Our techniques are general and can be applied to both Deep Q Networks (DQN) and Deep Deterministic Policy Gradient (DDPG) algorithms for discrete and continuous action control problems. We demonstrate that our proposed training procedure significantly improves the robustness of DQN and DDPG agents under a suite of strong white-box attacks on observations, including a few novel attacks we specifically craft. Additionally, our training procedure can produce provable certificates for the robustness of a Deep RL agent.

Robustness Verification of Tree-based Models

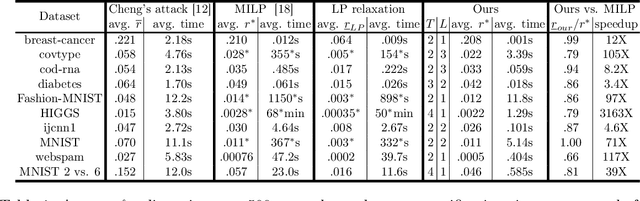
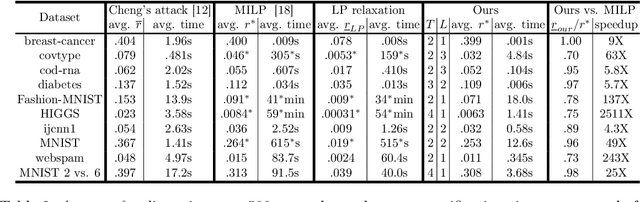
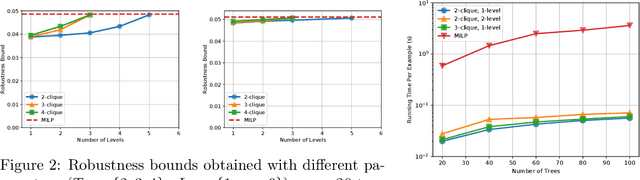
We study the robustness verification problem for tree-based models, including decision trees, random forests (RFs) and gradient boosted decision trees (GBDTs). Formal robustness verification of decision tree ensembles involves finding the exact minimal adversarial perturbation or a guaranteed lower bound of it. Existing approaches find the minimal adversarial perturbation by a mixed integer linear programming (MILP) problem, which takes exponential time so is impractical for large ensembles. Although this verification problem is NP-complete in general, we give a more precise complexity characterization. We show that there is a simple linear time algorithm for verifying a single tree, and for tree ensembles, the verification problem can be cast as a max-clique problem on a multi-partite graph with bounded boxicity. For low dimensional problems when boxicity can be viewed as constant, this reformulation leads to a polynomial time algorithm. For general problems, by exploiting the boxicity of the graph, we develop an efficient multi-level verification algorithm that can give tight lower bounds on the robustness of decision tree ensembles, while allowing iterative improvement and any-time termination. OnRF/GBDT models trained on 10 datasets, our algorithm is hundreds of times faster than the previous approach that requires solving MILPs, and is able to give tight robustness verification bounds on large GBDTs with hundreds of deep trees.

Towards Stable and Efficient Training of Verifiably Robust Neural Networks

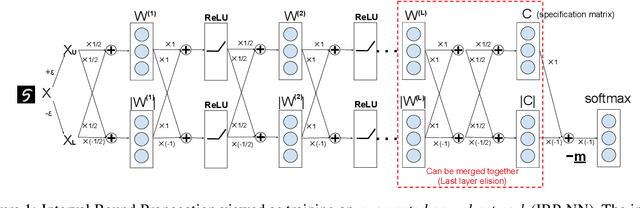
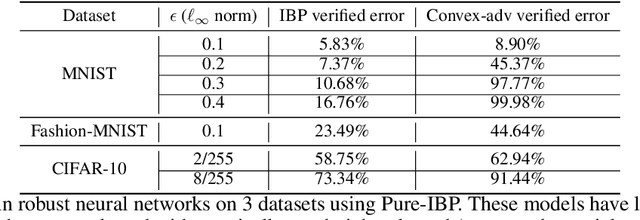
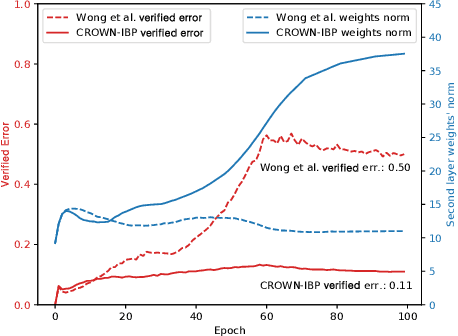
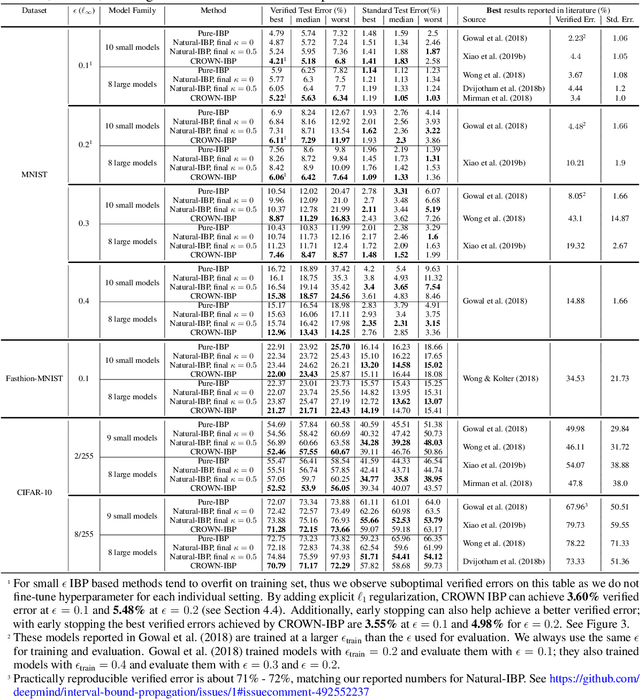
Training neural networks with verifiable robustness guarantees is challenging. Several existing successful approaches utilize relatively tight linear relaxation based bounds of neural network outputs, but they can slow down training by a factor of hundreds and over-regularize the network. Meanwhile, interval bound propagation (IBP) based training is efficient and significantly outperform linear relaxation based methods on some tasks, yet it suffers from stability issues since the bounds are much looser. In this paper, we first interpret IBP training as training an augmented network which computes non-linear bounds, thus explaining its good performance. We then propose a new certified adversarial training method, CROWN-IBP, by combining the fast IBP bounds in the forward pass and a tight linear relaxation based bound, CROWN, in the backward pass. The proposed method is computationally efficient and consistently outperforms IBP baselines on training verifiably robust neural networks. We conduct large scale experiments using 53 models on MNIST, Fashion-MNIST and CIFAR datasets. On MNIST with $\epsilon=0.3$ and $\epsilon=0.4$ ($\ell_\infty$ norm distortion) we achieve 7.46\% and 12.96\% verified error on test set, respectively, outperforming previous certified defense methods.

Robust Decision Trees Against Adversarial Examples

Although adversarial examples and model robustness have been extensively studied in the context of linear models and neural networks, research on this issue in tree-based models and how to make tree-based models robust against adversarial examples is still limited. In this paper, we show that tree based models are also vulnerable to adversarial examples and develop a novel algorithm to learn robust trees. At its core, our method aims to optimize the performance under the worst-case perturbation of input features, which leads to a max-min saddle point problem. Incorporating this saddle point objective into the decision tree building procedure is non-trivial due to the discrete nature of trees --- a naive approach to finding the best split according to this saddle point objective will take exponential time. To make our approach practical and scalable, we propose efficient tree building algorithms by approximating the inner minimizer in this saddle point problem, and present efficient implementations for classical information gain based trees as well as state-of-the-art tree boosting models such as XGBoost. Experimental results on real world datasets demonstrate that the proposed algorithms can substantially improve the robustness of tree-based models against adversarial examples.

The Limitations of Adversarial Training and the Blind-Spot Attack

The adversarial training procedure proposed by Madry et al. (2018) is one of the most effective methods to defend against adversarial examples in deep neural networks (DNNs). In our paper, we shed some lights on the practicality and the hardness of adversarial training by showing that the effectiveness (robustness on test set) of adversarial training has a strong correlation with the distance between a test point and the manifold of training data embedded by the network. Test examples that are relatively far away from this manifold are more likely to be vulnerable to adversarial attacks. Consequentially, an adversarial training based defense is susceptible to a new class of attacks, the "blind-spot attack", where the input images reside in "blind-spots" (low density regions) of the empirical distribution of training data but is still on the ground-truth data manifold. For MNIST, we found that these blind-spots can be easily found by simply scaling and shifting image pixel values. Most importantly, for large datasets with high dimensional and complex data manifold (CIFAR, ImageNet, etc), the existence of blind-spots in adversarial training makes defending on any valid test examples difficult due to the curse of dimensionality and the scarcity of training data. Additionally, we find that blind-spots also exist on provable defenses including (Wong & Kolter, 2018) and (Sinha et al., 2018) because these trainable robustness certificates can only be practically optimized on a limited set of training data.

Towards Fast Computation of Certified Robustness for ReLU Networks

Verifying the robustness property of a general Rectified Linear Unit (ReLU) network is an NP-complete problem [Katz, Barrett, Dill, Julian and Kochenderfer CAV17]. Although finding the exact minimum adversarial distortion is hard, giving a certified lower bound of the minimum distortion is possible. Current available methods of computing such a bound are either time-consuming or delivering low quality bounds that are too loose to be useful. In this paper, we exploit the special structure of ReLU networks and provide two computationally efficient algorithms Fast-Lin and Fast-Lip that are able to certify non-trivial lower bounds of minimum distortions, by bounding the ReLU units with appropriate linear functions Fast-Lin, or by bounding the local Lipschitz constant Fast-Lip. Experiments show that (1) our proposed methods deliver bounds close to (the gap is 2-3X) exact minimum distortion found by Reluplex in small MNIST networks while our algorithms are more than 10,000 times faster; (2) our methods deliver similar quality of bounds (the gap is within 35% and usually around 10%; sometimes our bounds are even better) for larger networks compared to the methods based on solving linear programming problems but our algorithms are 33-14,000 times faster; (3) our method is capable of solving large MNIST and CIFAR networks up to 7 layers with more than 10,000 neurons within tens of seconds on a single CPU core. In addition, we show that, in fact, there is no polynomial time algorithm that can approximately find the minimum $\ell_1$ adversarial distortion of a ReLU network with a $0.99\ln n$ approximation ratio unless $\mathsf{NP}$=$\mathsf{P}$, where $n$ is the number of neurons in the network.