Lookahead Sample Reward Guidance for Test-Time Scaling of Diffusion Models

Diffusion models have demonstrated strong generative performance; however, generated samples often fail to fully align with human intent. This paper studies a test-time scaling method that enables sampling from regions with higher human-aligned reward values. Existing gradient guidance methods approximate the expected future reward (EFR) at an intermediate particle $\mathbf{x}_t$ using a Taylor approximation, but this approximation at each time step incurs high computational cost due to sequential neural backpropagation. We show that the EFR at any $\mathbf{x}_t$ can be computed using only marginal samples from a pre-trained diffusion model. The proposed EFR formulation detaches the neural dependency between $\mathbf{x}_t$ and the EFR, enabling closed-form guidance computation without neural backpropagation. To further improve efficiency, we introduce lookahead sampling to collect marginal samples. For final sample generation, we use an accurate solver that guides particles toward high-reward lookahead samples. We refer to this sampling scheme as LiDAR sampling. LiDAR achieves substantial performance improvements using only three samples with a 3-step lookahead solver, exhibiting steep performance gains as lookahead accuracy and sample count increase; notably, it reaches the same GenEval performance as the latest gradient guidance method for SDXL with a 9.5x speedup.

Distilling Dataset into Neural Field

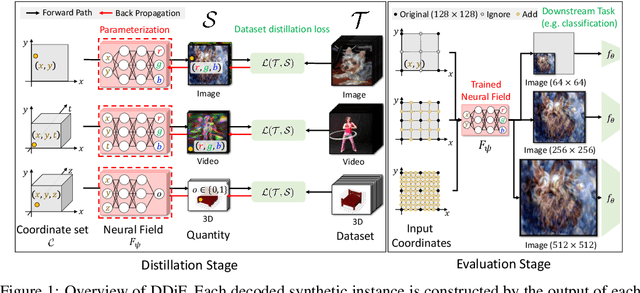
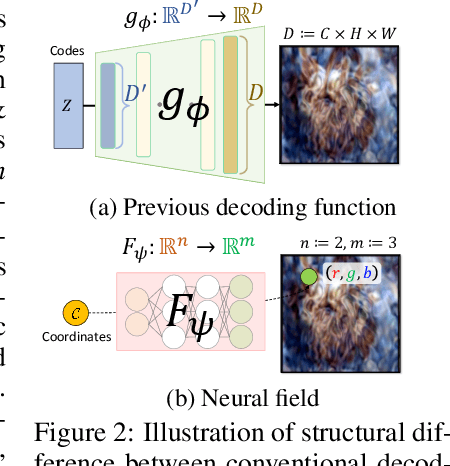
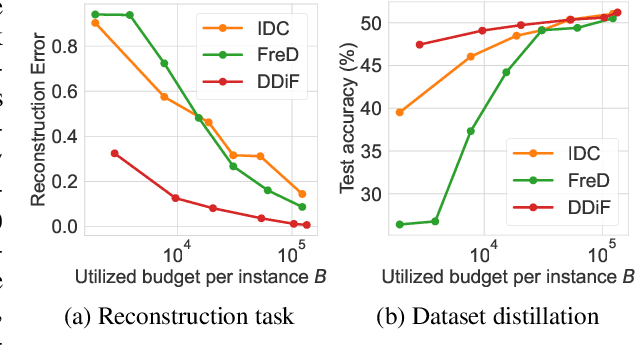
Utilizing a large-scale dataset is essential for training high-performance deep learning models, but it also comes with substantial computation and storage costs. To overcome these challenges, dataset distillation has emerged as a promising solution by compressing the large-scale dataset into a smaller synthetic dataset that retains the essential information needed for training. This paper proposes a novel parameterization framework for dataset distillation, coined Distilling Dataset into Neural Field (DDiF), which leverages the neural field to store the necessary information of the large-scale dataset. Due to the unique nature of the neural field, which takes coordinates as input and output quantity, DDiF effectively preserves the information and easily generates various shapes of data. We theoretically confirm that DDiF exhibits greater expressiveness than some previous literature when the utilized budget for a single synthetic instance is the same. Through extensive experiments, we demonstrate that DDiF achieves superior performance on several benchmark datasets, extending beyond the image domain to include video, audio, and 3D voxel. We release the code at https://github.com/aailab-kaist/DDiF.

Diffusion Rejection Sampling

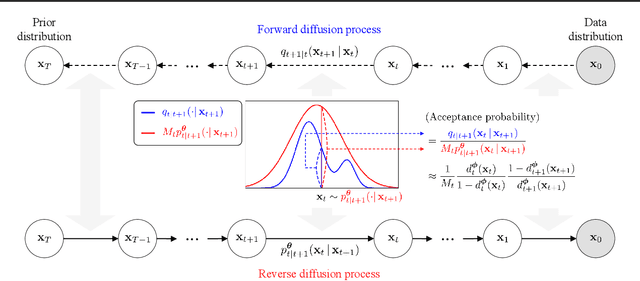
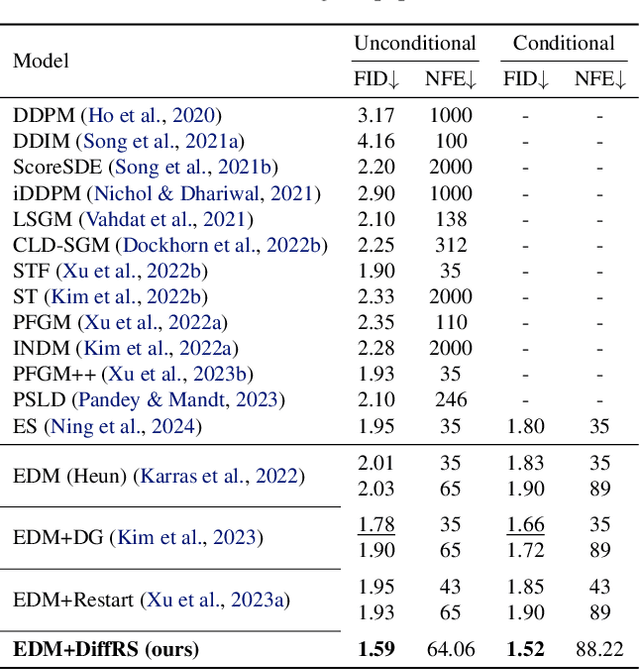
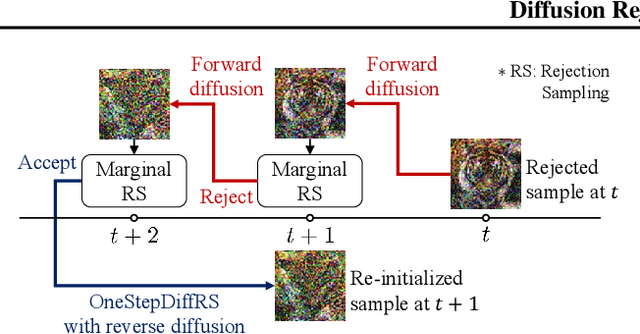
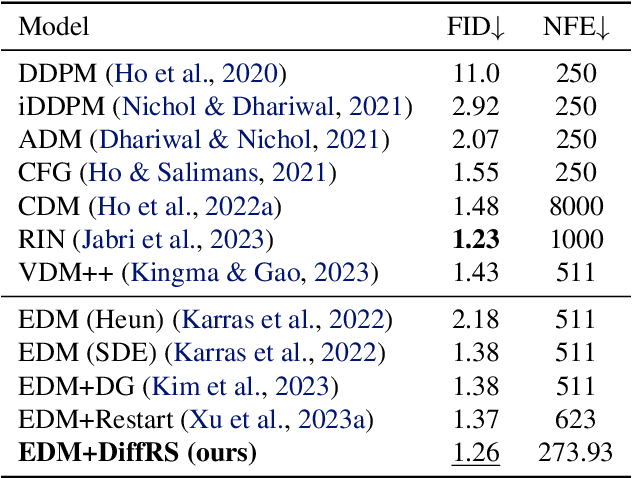
Recent advances in powerful pre-trained diffusion models encourage the development of methods to improve the sampling performance under well-trained diffusion models. This paper introduces Diffusion Rejection Sampling (DiffRS), which uses a rejection sampling scheme that aligns the sampling transition kernels with the true ones at each timestep. The proposed method can be viewed as a mechanism that evaluates the quality of samples at each intermediate timestep and refines them with varying effort depending on the sample. Theoretical analysis shows that DiffRS can achieve a tighter bound on sampling error compared to pre-trained models. Empirical results demonstrate the state-of-the-art performance of DiffRS on the benchmark datasets and the effectiveness of DiffRS for fast diffusion samplers and large-scale text-to-image diffusion models. Our code is available at https://github.com/aailabkaist/DiffRS.

Frequency Domain-based Dataset Distillation

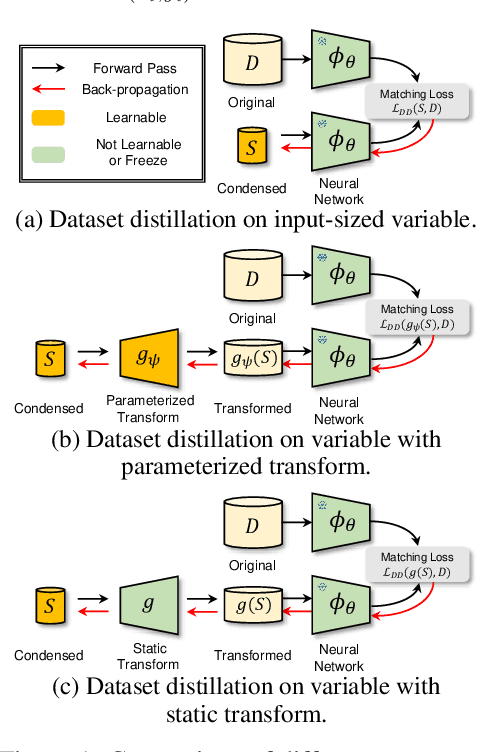
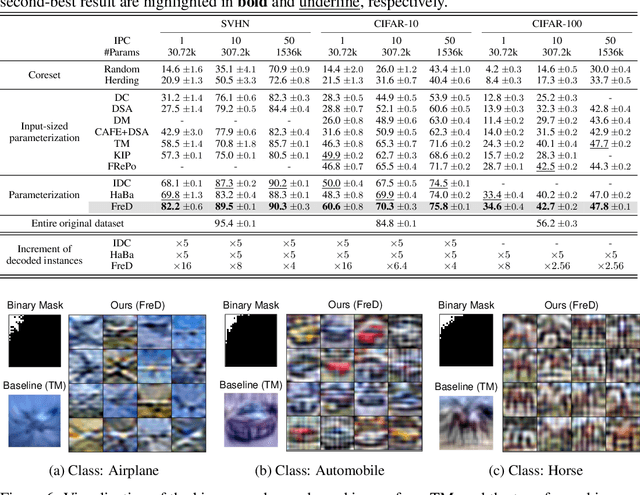
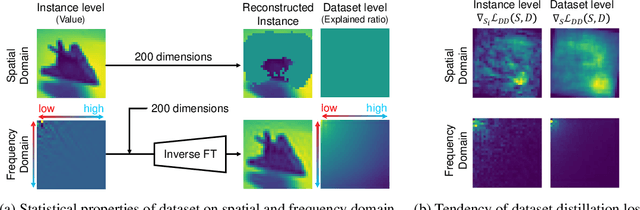
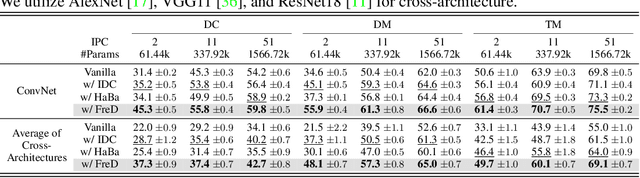
This paper presents FreD, a novel parameterization method for dataset distillation, which utilizes the frequency domain to distill a small-sized synthetic dataset from a large-sized original dataset. Unlike conventional approaches that focus on the spatial domain, FreD employs frequency-based transforms to optimize the frequency representations of each data instance. By leveraging the concentration of spatial domain information on specific frequency components, FreD intelligently selects a subset of frequency dimensions for optimization, leading to a significant reduction in the required budget for synthesizing an instance. Through the selection of frequency dimensions based on the explained variance, FreD demonstrates both theoretical and empirical evidence of its ability to operate efficiently within a limited budget, while better preserving the information of the original dataset compared to conventional parameterization methods. Furthermore, based on the orthogonal compatibility of FreD with existing methods, we confirm that FreD consistently improves the performances of existing distillation methods over the evaluation scenarios with different benchmark datasets. We release the code at https://github.com/sdh0818/FreD.

Loss-Curvature Matching for Dataset Selection and Condensation

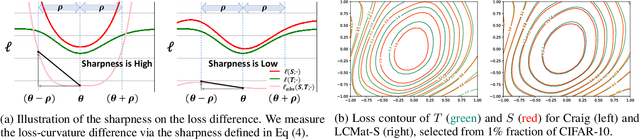
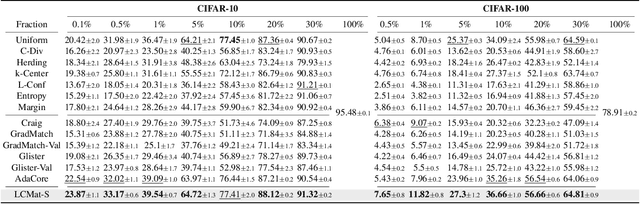
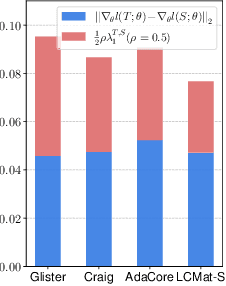
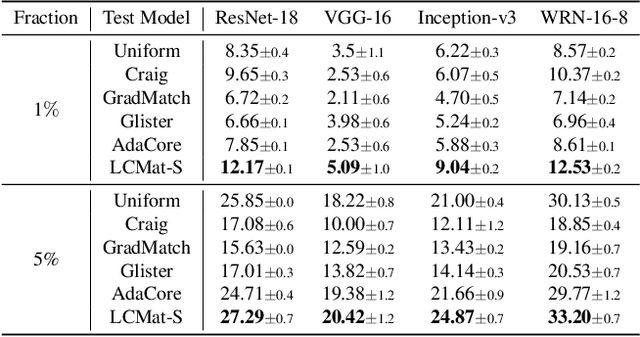
Training neural networks on a large dataset requires substantial computational costs. Dataset reduction selects or synthesizes data instances based on the large dataset, while minimizing the degradation in generalization performance from the full dataset. Existing methods utilize the neural network during the dataset reduction procedure, so the model parameter becomes important factor in preserving the performance after reduction. By depending upon the importance of parameters, this paper introduces a new reduction objective, coined LCMat, which Matches the Loss Curvatures of the original dataset and reduced dataset over the model parameter space, more than the parameter point. This new objective induces a better adaptation of the reduced dataset on the perturbed parameter region than the exact point matching. Particularly, we identify the worst case of the loss curvature gap from the local parameter region, and we derive the implementable upper bound of such worst-case with theoretical analyses. Our experiments on both coreset selection and condensation benchmarks illustrate that LCMat shows better generalization performances than existing baselines.