Learning Coordinate-based Convolutional Kernels for Continuous SE(3) Equivariant and Efficient Point Cloud Analysis

A symmetry on rigid motion is one of the salient factors in efficient learning of 3D point cloud problems. Group convolution has been a representative method to extract equivariant features, but its realizations have struggled to retain both rigorous symmetry and scalability simultaneously. We advocate utilizing the intertwiner framework to resolve this trade-off, but previous works on it, which did not achieve complete SE(3) symmetry or scalability to large-scale problems, necessitate a more advanced kernel architecture. We present Equivariant Coordinate-based Kernel Convolution, or ECKConv. It acquires SE(3) equivariance from the kernel domain defined in a double coset space, and its explicit kernel design using coordinate-based networks enhances its learning capability and memory efficiency. The experiments on diverse point cloud tasks, e.g., classification, pose registration, part segmentation, and large-scale semantic segmentation, validate the rigid equivariance, memory scalability, and outstanding performance of ECKConv compared to state-of-the-art equivariant methods.

Voronoi-based Second-order Descriptor with Whitened Metric in LiDAR Place Recognition

The pooling layer plays a vital role in aggregating local descriptors into the metrizable global descriptor in the LiDAR Place Recognition (LPR). In particular, the second-order pooling is capable of capturing higher-order interactions among local descriptors. However, its existing methods in the LPR adhere to conventional implementations and post-normalization, and incur the descriptor unsuitable for Euclidean distancing. Based on the recent interpretation that associates NetVLAD with the second-order statistics, we propose to integrate second-order pooling with the inductive bias from Voronoi cells. Our novel pooling method aggregates local descriptors to form the second-order matrix and whitens the global descriptor to implicitly measure the Mahalanobis distance while conserving the cluster property from Voronoi cells, addressing its numerical instability during learning with diverse techniques. We demonstrate its performance gains through the experiments conducted on the Oxford Robotcar and Wild-Places benchmarks and analyze the numerical effect of the proposed whitening algorithm.

Variational Online Mirror Descent for Robust Learning in Schrödinger Bridge

Sch\"odinger bridge (SB) has evolved into a universal class of probabilistic generative models. In practice, however, estimated learning signals are often uncertain, and the reliability promised by existing methods is often based on speculative optimal-case scenarios. Recent studies regarding the Sinkhorn algorithm through mirror descent (MD) have gained attention, revealing geometric insights into solution acquisition of the SB problems. In this paper, we propose a variational online MD (OMD) framework for the SB problems, which provides further stability to SB solvers. We formally prove convergence and a regret bound for the novel OMD formulation of SB acquisition. As a result, we propose a simulation-free SB algorithm called Variational Mirrored Schr\"odinger Bridge (VMSB) by utilizing the Wasserstein-Fisher-Rao geometry of the Gaussian mixture parameterization for Schr\"odinger potentials. Based on the Wasserstein gradient flow theory, the algorithm offers tractable learning dynamics that precisely approximate each OMD step. In experiments, we validate the performance of the proposed VMSB algorithm across an extensive suite of benchmarks. VMSB consistently outperforms contemporary SB solvers on a range of SB problems, demonstrating the robustness predicted by our theory.

DUEL: Duplicate Elimination on Active Memory for Self-Supervised Class-Imbalanced Learning

Recent machine learning algorithms have been developed using well-curated datasets, which often require substantial cost and resources. On the other hand, the direct use of raw data often leads to overfitting towards frequently occurring class information. To address class imbalances cost-efficiently, we propose an active data filtering process during self-supervised pre-training in our novel framework, Duplicate Elimination (DUEL). This framework integrates an active memory inspired by human working memory and introduces distinctiveness information, which measures the diversity of the data in the memory, to optimize both the feature extractor and the memory. The DUEL policy, which replaces the most duplicated data with new samples, aims to enhance the distinctiveness information in the memory and thereby mitigate class imbalances. We validate the effectiveness of the DUEL framework in class-imbalanced environments, demonstrating its robustness and providing reliable results in downstream tasks. We also analyze the role of the DUEL policy in the training process through various metrics and visualizations.

EXOT: Exit-aware Object Tracker for Safe Robotic Manipulation of Moving Object

Current robotic hand manipulation narrowly operates with objects in predictable positions in limited environments. Thus, when the location of the target object deviates severely from the expected location, a robot sometimes responds in an unexpected way, especially when it operates with a human. For safe robot operation, we propose the EXit-aware Object Tracker (EXOT) on a robot hand camera that recognizes an object's absence during manipulation. The robot decides whether to proceed by examining the tracker's bounding box output containing the target object. We adopt an out-of-distribution classifier for more accurate object recognition since trackers can mistrack a background as a target object. To the best of our knowledge, our method is the first approach of applying an out-of-distribution classification technique to a tracker output. We evaluate our method on the first-person video benchmark dataset, TREK-150, and on the custom dataset, RMOT-223, that we collect from the UR5e robot. Then we test our tracker on the UR5e robot in real-time with a conveyor-belt sushi task, to examine the tracker's ability to track target dishes and to determine the exit status. Our tracker shows 38% higher exit-aware performance than a baseline method. The dataset and the code will be released at https://github.com/hskAlena/EXOT.

DUEL: Adaptive Duplicate Elimination on Working Memory for Self-Supervised Learning

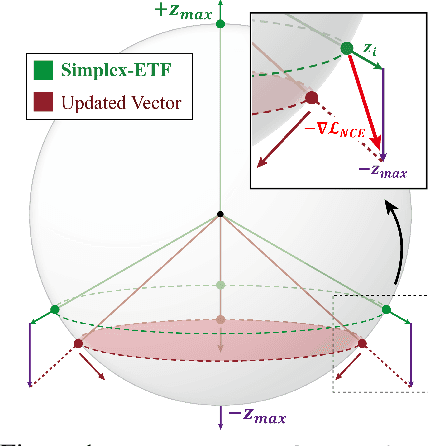
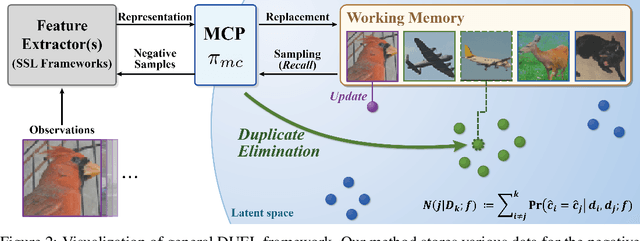
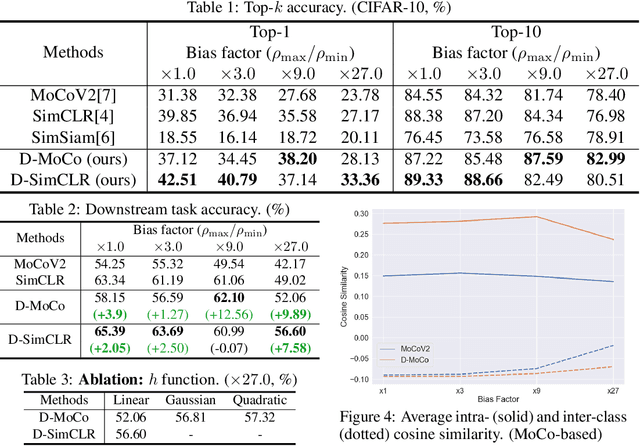
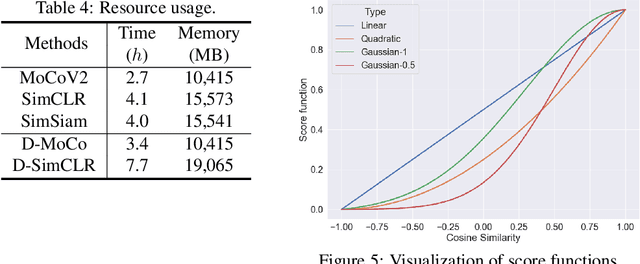
In Self-Supervised Learning (SSL), it is known that frequent occurrences of the collision in which target data and its negative samples share the same class can decrease performance. Especially in real-world data such as crawled data or robot-gathered observations, collisions may occur more often due to the duplicates in the data. To deal with this problem, we claim that sampling negative samples from the adaptively debiased distribution in the memory makes the model more stable than sampling from a biased dataset directly. In this paper, we introduce a novel SSL framework with adaptive Duplicate Elimination (DUEL) inspired by the human working memory. The proposed framework successfully prevents the downstream task performance from degradation due to a dramatic inter-class imbalance.

Robust Imitation via Mirror Descent Inverse Reinforcement Learning

Recently, adversarial imitation learning has shown a scalable reward acquisition method for inverse reinforcement learning (IRL) problems. However, estimated reward signals often become uncertain and fail to train a reliable statistical model since the existing methods tend to solve hard optimization problems directly. Inspired by a first-order optimization method called mirror descent, this paper proposes to predict a sequence of reward functions, which are iterative solutions for a constrained convex problem. IRL solutions derived by mirror descent are tolerant to the uncertainty incurred by target density estimation since the amount of reward learning is regulated with respect to local geometric constraints. We prove that the proposed mirror descent update rule ensures robust minimization of a Bregman divergence in terms of a rigorous regret bound of $\mathcal{O}(1/T)$ for step sizes $\{\eta_t\}_{t=1}^{T}$. Our IRL method was applied on top of an adversarial framework, and it outperformed existing adversarial methods in an extensive suite of benchmarks.