A Knowledge-Informed Deep Learning Paradigm for Generalizable and Stability-Optimized Car-Following Models

Car-following models (CFMs) are fundamental to traffic flow analysis and autonomous driving. Although calibrated physics-based and trained data-driven CFMs can replicate human driving behavior, their reliance on specific datasets limits generalization across diverse scenarios and reduces reliability in real-world deployment. Moreover, these models typically focus on behavioral fidelity and do not support the explicit optimization of local and string stability, which are increasingly important for the safe and efficient operation of autonomous vehicles (AVs). To address these limitations, we propose a Knowledge-Informed Deep Learning (KIDL) paradigm that distills the generalization capabilities of pre-trained Large Language Models (LLMs) into a lightweight and stability-aware neural architecture. LLMs are used to extract fundamental car-following knowledge beyond dataset-specific patterns, and this knowledge is transferred to a reliable, tractable, and computationally efficient model through knowledge distillation. KIDL also incorporates stability constraints directly into its training objective, ensuring that the resulting model not only emulates human-like behavior but also satisfies the local and string stability requirements essential for real-world AV deployment. We evaluate KIDL on the real-world NGSIM and HighD datasets, comparing its performance with representative physics-based, data-driven, and hybrid CFMs. Both empirical and theoretical results consistently demonstrate KIDL's superior behavioral generalization and traffic flow stability, offering a robust and scalable solution for next-generation traffic systems.

Knowledge-data fusion oriented traffic state estimation: A stochastic physics-informed deep learning approach

Physics-informed deep learning (PIDL)-based models have recently garnered remarkable success in traffic state estimation (TSE). However, the prior knowledge used to guide regularization training in current mainstream architectures is based on deterministic physical models. The drawback is that a solely deterministic model fails to capture the universally observed traffic flow dynamic scattering effect, thereby yielding unreliable outcomes for traffic control. This study, for the first time, proposes stochastic physics-informed deep learning (SPIDL) for traffic state estimation. The idea behind such SPIDL is simple and is based on the fact that a stochastic fundamental diagram provides the entire range of possible speeds for any given density with associated probabilities. Specifically, we select percentile-based fundamental diagram and distribution-based fundamental diagram as stochastic physics knowledge, and design corresponding physics-uninformed neural networks for effective fusion, thereby realizing two specific SPIDL models, namely \text{$\alpha$}-SPIDL and \text{$\cal B$}-SPIDL. The main contribution of SPIDL lies in addressing the "overly centralized guidance" caused by the one-to-one speed-density relationship in deterministic models during neural network training, enabling the network to digest more reliable knowledge-based constraints.Experiments on the real-world dataset indicate that proposed SPIDL models achieve accurate traffic state estimation in sparse data scenarios. More importantly, as expected, SPIDL models reproduce well the scattering effect of field observations, demonstrating the effectiveness of fusing stochastic physics model knowledge with deep learning frameworks.

Inferring Heterogeneous Treatment Effects of Crashes on Highway Traffic: A Doubly Robust Causal Machine Learning Approach

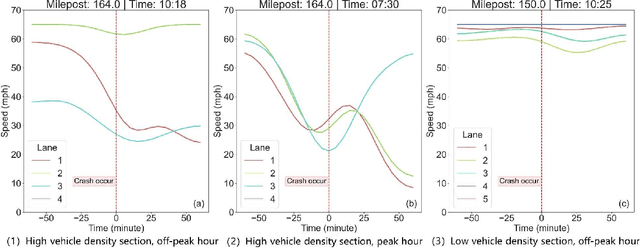
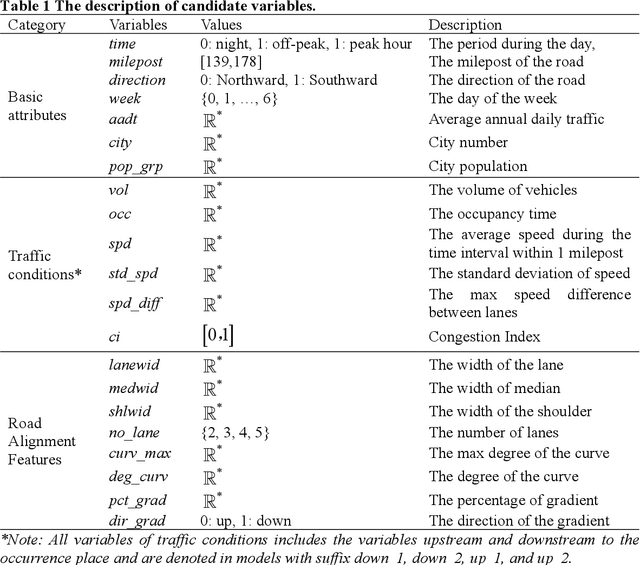
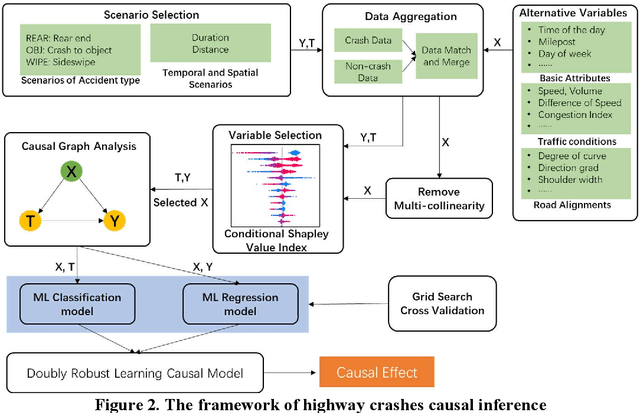
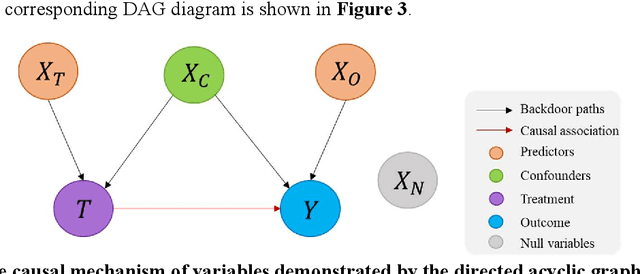
Highway traffic crashes exert a considerable impact on both transportation systems and the economy. In this context, accurate and dependable emergency responses are crucial for effective traffic management. However, the influence of crashes on traffic status varies across diverse factors and may be biased due to selection bias. Therefore, there arises a necessity to accurately estimate the heterogeneous causal effects of crashes, thereby providing essential insights to facilitate individual-level emergency decision-making. This paper proposes a novel causal machine learning framework to estimate the causal effect of different types of crashes on highway speed. The Neyman-Rubin Causal Model (RCM) is employed to formulate this problem from a causal perspective. The Conditional Shapley Value Index (CSVI) is proposed based on causal graph theory to filter adverse variables, and the Structural Causal Model (SCM) is then adopted to define the statistical estimand for causal effects. The treatment effects are estimated by Doubly Robust Learning (DRL) methods, which combine doubly robust causal inference with classification and regression machine learning models. Experimental results from 4815 crashes on Highway Interstate 5 in Washington State reveal the heterogeneous treatment effects of crashes at varying distances and durations. The rear-end crashes cause more severe congestion and longer durations than other types of crashes, and the sideswipe crashes have the longest delayed impact. Additionally, the findings show that rear-end crashes affect traffic greater at night, while crash to objects has the most significant influence during peak hours. Statistical hypothesis tests, error metrics based on matched "counterfactual outcomes", and sensitive analyses are employed for assessment, and the results validate the accuracy and effectiveness of our method.