Finding Low-Rank Solutions via Non-Convex Matrix Factorization, Efficiently and Provably

A rank-$r$ matrix $X \in \mathbb{R}^{m \times n}$ can be written as a product $U V^\top$, where $U \in \mathbb{R}^{m \times r}$ and $V \in \mathbb{R}^{n \times r}$. One could exploit this observation in optimization: e.g., consider the minimization of a convex function $f(X)$ over rank-$r$ matrices, where the set of rank-$r$ matrices is modeled via the factorization $UV^\top$. Though such parameterization reduces the number of variables, and is more computationally efficient (of particular interest is the case $r \ll \min\{m, n\}$), it comes at a cost: $f(UV^\top)$ becomes a non-convex function w.r.t. $U$ and $V$. We study such parameterization for optimization of generic convex objectives $f$, and focus on first-order, gradient descent algorithmic solutions. We propose the Bi-Factored Gradient Descent (BFGD) algorithm, an efficient first-order method that operates on the $U, V$ factors. We show that when $f$ is (restricted) smooth, BFGD has local sublinear convergence, and linear convergence when $f$ is both (restricted) smooth and (restricted) strongly convex. For several key applications, we provide simple and efficient initialization schemes that provide approximate solutions good enough for the above convergence results to hold.

Provable Burer-Monteiro factorization for a class of norm-constrained matrix problems

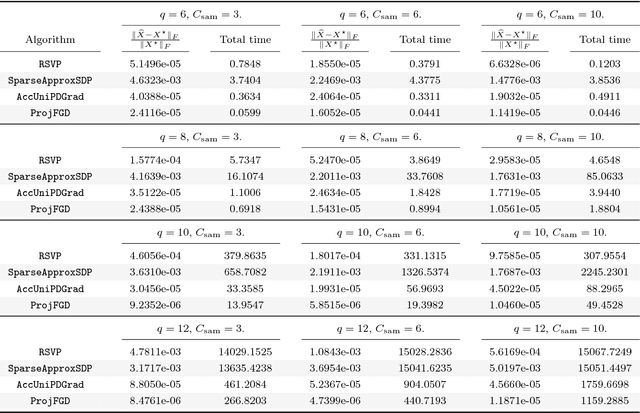
We study the projected gradient descent method on low-rank matrix problems with a strongly convex objective. We use the Burer-Monteiro factorization approach to implicitly enforce low-rankness; such factorization introduces non-convexity in the objective. We focus on constraint sets that include both positive semi-definite (PSD) constraints and specific matrix norm-constraints. Such criteria appear in quantum state tomography and phase retrieval applications. We show that non-convex projected gradient descent favors local linear convergence in the factored space. We build our theory on a novel descent lemma, that non-trivially extends recent results on the unconstrained problem. The resulting algorithm is Projected Factored Gradient Descent, abbreviated as ProjFGD, and shows superior performance compared to state of the art on quantum state tomography and sparse phase retrieval applications.

Non-square matrix sensing without spurious local minima via the Burer-Monteiro approach

We consider the non-square matrix sensing problem, under restricted isometry property (RIP) assumptions. We focus on the non-convex formulation, where any rank-$r$ matrix $X \in \mathbb{R}^{m \times n}$ is represented as $UV^\top$, where $U \in \mathbb{R}^{m \times r}$ and $V \in \mathbb{R}^{n \times r}$. In this paper, we complement recent findings on the non-convex geometry of the analogous PSD setting [5], and show that matrix factorization does not introduce any spurious local minima, under RIP.

Fast Algorithms for Robust PCA via Gradient Descent

We consider the problem of Robust PCA in the fully and partially observed settings. Without corruptions, this is the well-known matrix completion problem. From a statistical standpoint this problem has been recently well-studied, and conditions on when recovery is possible (how many observations do we need, how many corruptions can we tolerate) via polynomial-time algorithms is by now understood. This paper presents and analyzes a non-convex optimization approach that greatly reduces the computational complexity of the above problems, compared to the best available algorithms. In particular, in the fully observed case, with $r$ denoting rank and $d$ dimension, we reduce the complexity from $\mathcal{O}(r^2d^2\log(1/\varepsilon))$ to $\mathcal{O}(rd^2\log(1/\varepsilon))$ -- a big savings when the rank is big. For the partially observed case, we show the complexity of our algorithm is no more than $\mathcal{O}(r^4d \log d \log(1/\varepsilon))$. Not only is this the best-known run-time for a provable algorithm under partial observation, but in the setting where $r$ is small compared to $d$, it also allows for near-linear-in-$d$ run-time that can be exploited in the fully-observed case as well, by simply running our algorithm on a subset of the observations.

Preference Completion: Large-scale Collaborative Ranking from Pairwise Comparisons

In this paper we consider the collaborative ranking setting: a pool of users each provides a small number of pairwise preferences between $d$ possible items; from these we need to predict preferences of the users for items they have not yet seen. We do so by fitting a rank $r$ score matrix to the pairwise data, and provide two main contributions: (a) we show that an algorithm based on convex optimization provides good generalization guarantees once each user provides as few as $O(r\log^2 d)$ pairwise comparisons -- essentially matching the sample complexity required in the related matrix completion setting (which uses actual numerical as opposed to pairwise information), and (b) we develop a large-scale non-convex implementation, which we call AltSVM, that trains a factored form of the matrix via alternating minimization (which we show reduces to alternating SVM problems), and scales and parallelizes very well to large problem settings. It also outperforms common baselines on many moderately large popular collaborative filtering datasets in both NDCG and in other measures of ranking performance.

Greedy Subspace Clustering

We consider the problem of subspace clustering: given points that lie on or near the union of many low-dimensional linear subspaces, recover the subspaces. To this end, one first identifies sets of points close to the same subspace and uses the sets to estimate the subspaces. As the geometric structure of the clusters (linear subspaces) forbids proper performance of general distance based approaches such as K-means, many model-specific methods have been proposed. In this paper, we provide new simple and efficient algorithms for this problem. Our statistical analysis shows that the algorithms are guaranteed exact (perfect) clustering performance under certain conditions on the number of points and the affinity between subspaces. These conditions are weaker than those considered in the standard statistical literature. Experimental results on synthetic data generated from the standard unions of subspaces model demonstrate our theory. We also show that our algorithm performs competitively against state-of-the-art algorithms on real-world applications such as motion segmentation and face clustering, with much simpler implementation and lower computational cost.