Structure-Preserving 3D Garment Modeling with Neural Sewing Machines

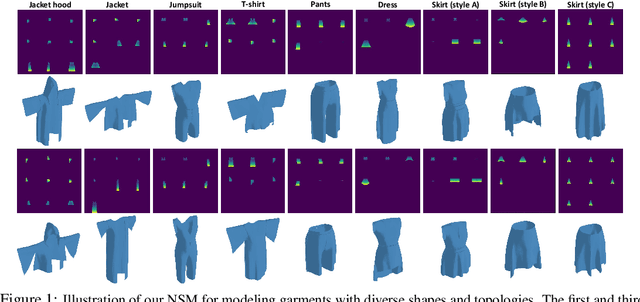
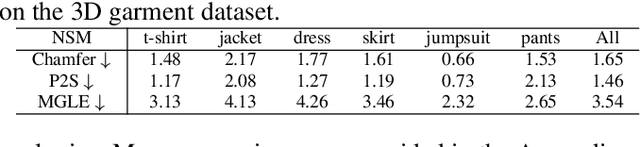
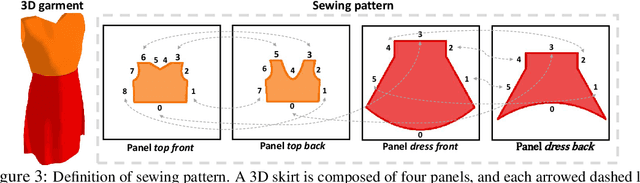
3D Garment modeling is a critical and challenging topic in the area of computer vision and graphics, with increasing attention focused on garment representation learning, garment reconstruction, and controllable garment manipulation, whereas existing methods were constrained to model garments under specific categories or with relatively simple topologies. In this paper, we propose a novel Neural Sewing Machine (NSM), a learning-based framework for structure-preserving 3D garment modeling, which is capable of learning representations for garments with diverse shapes and topologies and is successfully applied to 3D garment reconstruction and controllable manipulation. To model generic garments, we first obtain sewing pattern embedding via a unified sewing pattern encoding module, as the sewing pattern can accurately describe the intrinsic structure and the topology of the 3D garment. Then we use a 3D garment decoder to decode the sewing pattern embedding into a 3D garment using the UV-position maps with masks. To preserve the intrinsic structure of the predicted 3D garment, we introduce an inner-panel structure-preserving loss, an inter-panel structure-preserving loss, and a surface-normal loss in the learning process of our framework. We evaluate NSM on the public 3D garment dataset with sewing patterns with diverse garment shapes and categories. Extensive experiments demonstrate that the proposed NSM is capable of representing 3D garments under diverse garment shapes and topologies, realistically reconstructing 3D garments from 2D images with the preserved structure, and accurately manipulating the 3D garment categories, shapes, and topologies, outperforming the state-of-the-art methods by a clear margin.

Least squares surface reconstruction on arbitrary domains

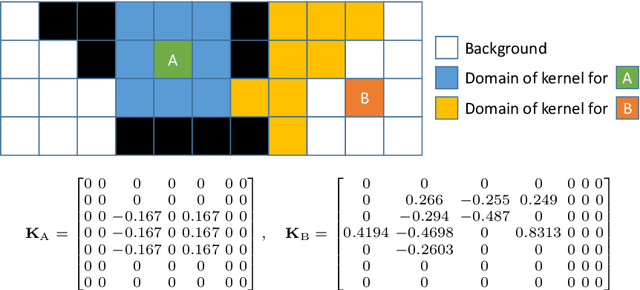
Almost universally in computer vision, when surface derivatives are required, they are computed using only first order accurate finite difference approximations. We propose a new method for computing numerical derivatives based on 2D Savitzky-Golay filters and K-nearest neighbour kernels. The resulting derivative matrices can be used for least squares surface reconstruction over arbitrary (even disconnected) domains in the presence of large noise and allowing for higher order polynomial local surface approximations. They are useful for a range of tasks including normal-from-depth (i.e. surface differentiation), height-from-normals (i.e. surface integration) and shape-from-x. We show how to write both orthographic or perspective height-from-normals as a linear least squares problem using the same formulation and avoiding a nonlinear change of variables in the perspective case. We demonstrate improved performance relative to state-of-the-art across these tasks on both synthetic and real data and make available an open source implementation of our method.

Depth from a polarisation + RGB stereo pair

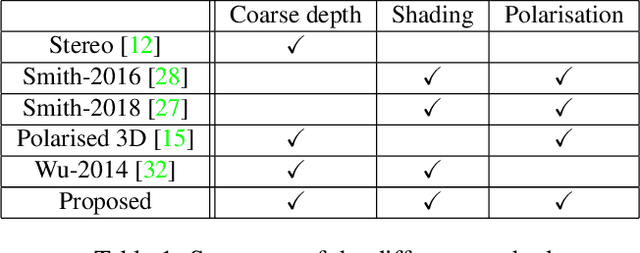
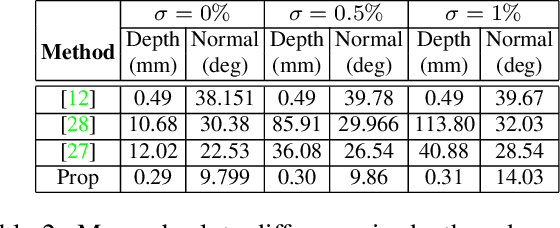
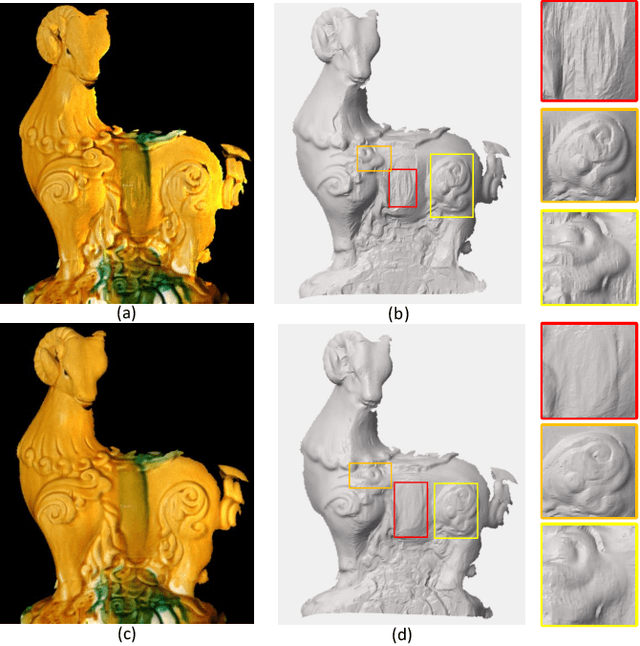
In this paper, we propose a hybrid depth imaging system in which a polarisation camera is augmented by a second image from a standard digital camera. For this modest increase in equipment complexity over conventional shape-from-polarisation, we obtain a number of benefits that enable us to overcome longstanding problems with the polarisation shape cue. The stereo cue provides a depth map which, although coarse, is metrically accurate. This is used as a guide surface for disambiguation of the polarisation surface normal estimates using a higher order graphical model. In turn, these are used to estimate diffuse albedo. By extending a previous shape-from-polarisation method to the perspective case, we show how to compute dense, detailed maps of absolute depth, while retaining a linear formulation. We show that our hybrid method is able to recover dense 3D geometry that is superior to state-of-the-art shape-from-polarisation or two view stereo alone.

Linear Differential Constraints for Photo-polarimetric Height Estimation

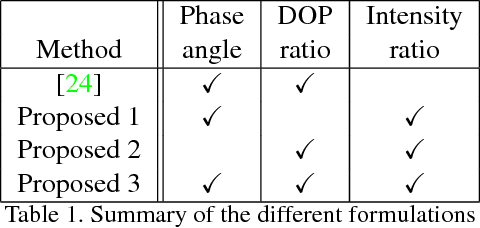
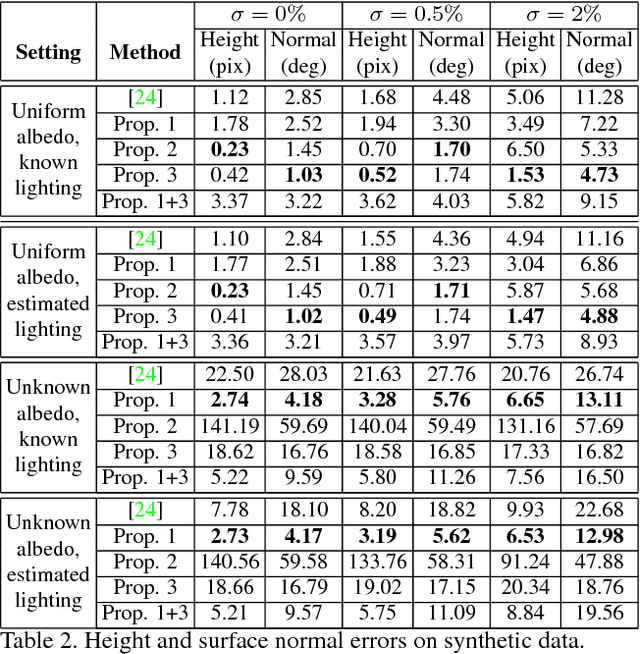
In this paper we present a differential approach to photo-polarimetric shape estimation. We propose several alternative differential constraints based on polarisation and photometric shading information and show how to express them in a unified partial differential system. Our method uses the image ratios technique to combine shading and polarisation information in order to directly reconstruct surface height, without first computing surface normal vectors. Moreover, we are able to remove the non-linearities so that the problem reduces to solving a linear differential problem. We also introduce a new method for estimating a polarisation image from multichannel data and, finally, we show it is possible to estimate the illumination directions in a two source setup, extending the method into an uncalibrated scenario. From a numerical point of view, we use a least-squares formulation of the discrete version of the problem. To the best of our knowledge, this is the first work to consider a unified differential approach to solve photo-polarimetric shape estimation directly for height. Numerical results on synthetic and real-world data confirm the effectiveness of our proposed method.