An overview of some mathematical techniques and problems linking 3D vision to 3D printing

Computer Vision and 3D printing have rapidly evolved in the last 10 years but interactions among them have been very limited so far, despite the fact that they share several mathematical techniques. We try to fill the gap presenting an overview of some techniques for Shape-from-Shading problems as well as for 3D printing with an emphasis on the approaches based on nonlinear partial differential equations and optimization. We also sketch possible couplings to complete the process of object manufacturing starting from one or more images of the object and ending with its final 3D print. We will give some practical examples of this procedure.

A High-Order Scheme for Image Segmentation via a modified Level-Set method

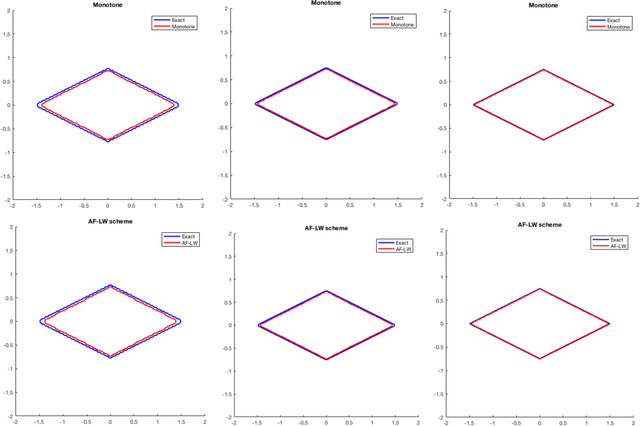
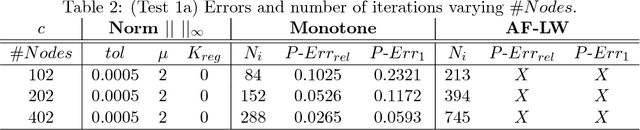
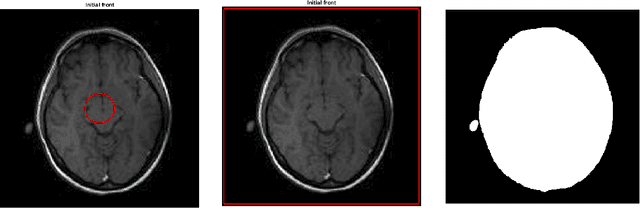
The method is based on an adaptive "filtered" scheme recently introduced by the authors. The main feature of the scheme is the possibility to stabilize an a priori unstable high-order scheme via a filter function which allows to combine a high-order scheme in the regularity regions and a monotone scheme elsewhere, in presence of singularities. The filtered scheme considered in this paper uses the local Lax-Friedrichs scheme as monotone scheme and the Lax-Wendroff scheme as high-order scheme but other couplings are possible. Moreover, we introduce also a modified velocity function for the level-set model used in segmentation, this velocity allows to obtain more accurate results with respect to other velocities proposed in the literature. Some numerical tests on synthetic and real images confirm the accuracy of the proposed method and the advantages given by the new velocity.

Linear Differential Constraints for Photo-polarimetric Height Estimation

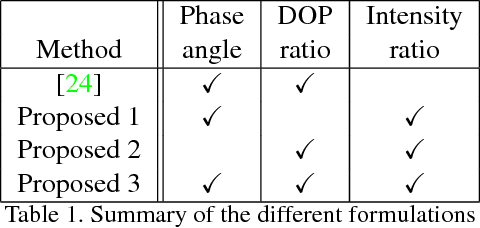
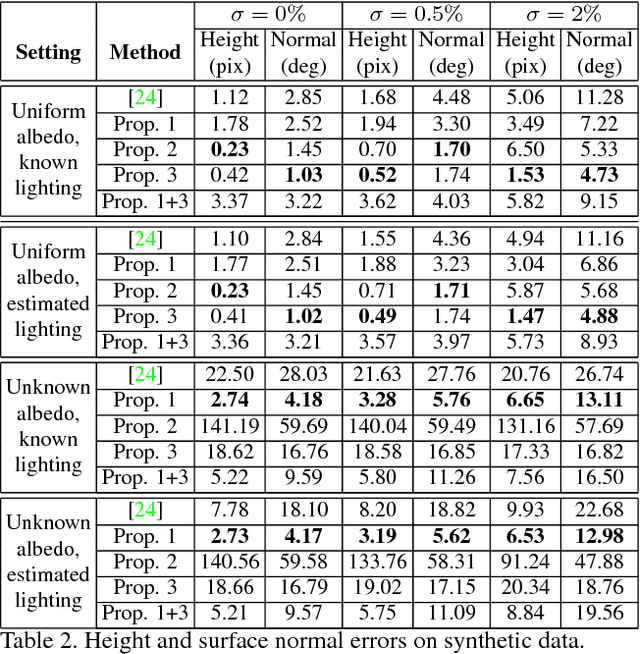
In this paper we present a differential approach to photo-polarimetric shape estimation. We propose several alternative differential constraints based on polarisation and photometric shading information and show how to express them in a unified partial differential system. Our method uses the image ratios technique to combine shading and polarisation information in order to directly reconstruct surface height, without first computing surface normal vectors. Moreover, we are able to remove the non-linearities so that the problem reduces to solving a linear differential problem. We also introduce a new method for estimating a polarisation image from multichannel data and, finally, we show it is possible to estimate the illumination directions in a two source setup, extending the method into an uncalibrated scenario. From a numerical point of view, we use a least-squares formulation of the discrete version of the problem. To the best of our knowledge, this is the first work to consider a unified differential approach to solve photo-polarimetric shape estimation directly for height. Numerical results on synthetic and real-world data confirm the effectiveness of our proposed method.

Analysis and approximation of some Shape-from-Shading models for non-Lambertian surfaces

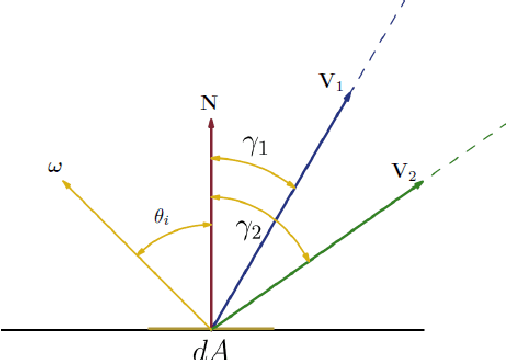
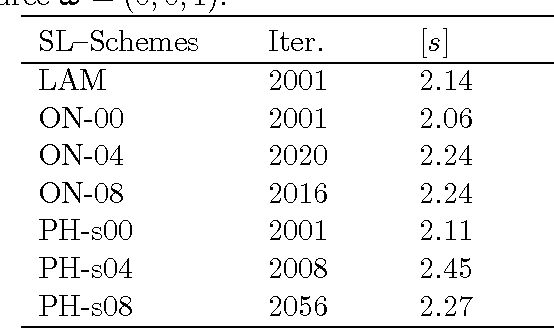
The reconstruction of a 3D object or a scene is a classical inverse problem in Computer Vision. In the case of a single image this is called the Shape-from-Shading (SfS) problem and it is known to be ill-posed even in a simplified version like the vertical light source case. A huge number of works deals with the orthographic SfS problem based on the Lambertian reflectance model, the most common and simplest model which leads to an eikonal type equation when the light source is on the vertical axis. In this paper we want to study non-Lambertian models since they are more realistic and suitable whenever one has to deal with different kind of surfaces, rough or specular. We will present a unified mathematical formulation of some popular orthographic non-Lambertian models, considering vertical and oblique light directions as well as different viewer positions. These models lead to more complex stationary nonlinear partial differential equations of Hamilton-Jacobi type which can be regarded as the generalization of the classical eikonal equation corresponding to the Lambertian case. However, all the equations corresponding to the models considered here (Oren-Nayar and Phong) have a similar structure so we can look for weak solutions to this class in the viscosity solution framework. Via this unified approach, we are able to develop a semi-Lagrangian approximation scheme for the Oren-Nayar and the Phong model and to prove a general convergence result. Numerical simulations on synthetic and real images will illustrate the effectiveness of this approach and the main features of the scheme, also comparing the results with previous results in the literature.