On the Interplay of Subset Selection and Informed Graph Neural Networks

Machine learning techniques paired with the availability of massive datasets dramatically enhance our ability to explore the chemical compound space by providing fast and accurate predictions of molecular properties. However, learning on large datasets is strongly limited by the availability of computational resources and can be infeasible in some scenarios. Moreover, the instances in the datasets may not yet be labelled and generating the labels can be costly, as in the case of quantum chemistry computations. Thus, there is a need to select small training subsets from large pools of unlabelled data points and to develop reliable ML methods that can effectively learn from small training sets. This work focuses on predicting the molecules atomization energy in the QM9 dataset. We investigate the advantages of employing domain knowledge-based data sampling methods for an efficient training set selection combined with informed ML techniques. In particular, we show how maximizing molecular diversity in the training set selection process increases the robustness of linear and nonlinear regression techniques such as kernel methods and graph neural networks. We also check the reliability of the predictions made by the graph neural network with a model-agnostic explainer based on the rate distortion explanation framework.

Learning Variational Models with Unrolling and Bilevel Optimization

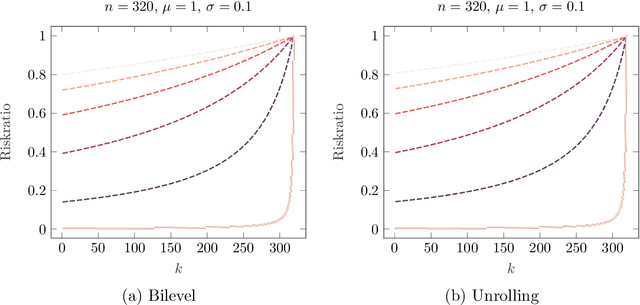
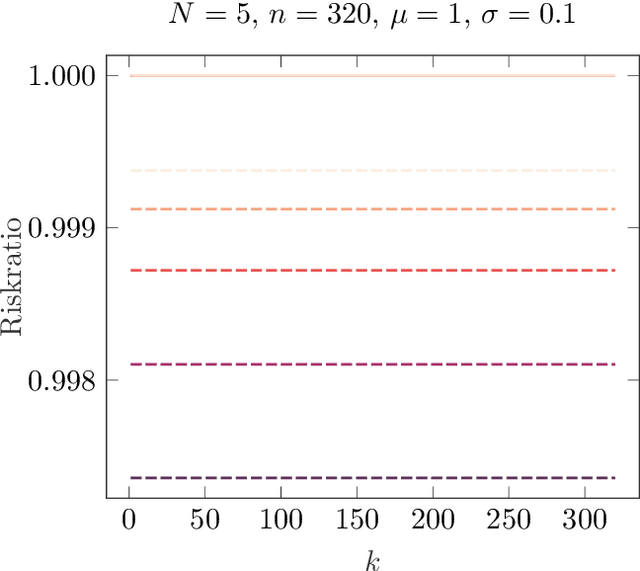
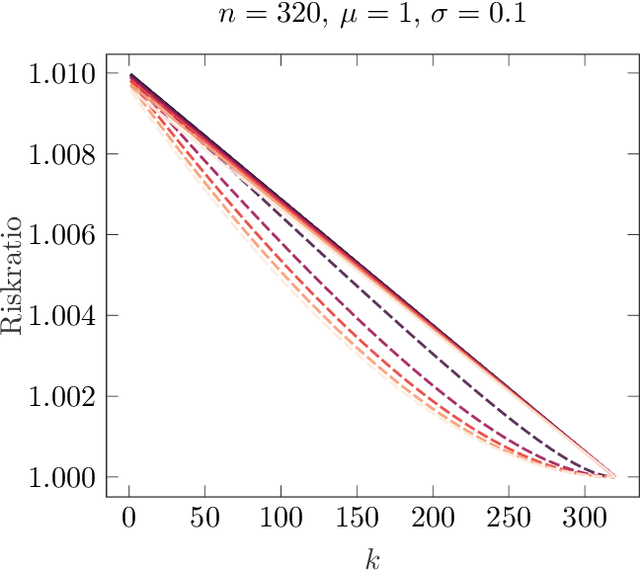
In this paper we consider the problem learning of variational models in the context of supervised learning via risk minimization. Our goal is to provide a deeper understanding of the two approaches of learning of variational models via bilevel optimization and via algorithm unrolling. The former considers the variational model as a lower level optimization problem below the risk minimization problem, while the latter replaces the lower level optimization problem by an algorithm that solves said problem approximately. Both approaches are used in practice, but, unrolling is much simpler from a computational point of view. To analyze and compare the two approaches, we consider a simple toy model, and compute all risks and the respective estimators explicitly. We show that unrolling can be better than the bilevel optimization approach, but also that the performance of unrolling can depend significantly on further parameters, sometimes in unexpected ways: While the stepsize of the unrolled algorithm matters a lot, the number of unrolled iterations only matters if the number is even or odd, and these two cases are notably different.

Non-stationary Douglas-Rachford and alternating direction method of multipliers: adaptive stepsizes and convergence

We revisit the classical Douglas-Rachford (DR) method for finding a zero of the sum of two maximal monotone operators. Since the practical performance of the DR method crucially depends on the stepsizes, we aim at developing an adaptive stepsize rule. To that end, we take a closer look at a linear case of the problem and use our findings to develop a stepsize strategy that eliminates the need for stepsize tuning. We analyze a general non-stationary DR scheme and prove its convergence for a convergent sequence of stepsizes with summable increments. This, in turn, proves the convergence of the method with the new adaptive stepsize rule. We also derive the related non-stationary alternating direction method of multipliers (ADMM) from such a non-stationary DR method. We illustrate the efficiency of the proposed methods on several numerical examples.

Denoising of image gradients and total generalized variation denoising

We revisit total variation denoising and study an augmented model where we assume that an estimate of the image gradient is available. We show that this increases the image reconstruction quality and derive that the resulting model resembles the total generalized variation denoising method, thus providing a new motivation for this model. Further, we propose to use a constraint denoising model and develop a variational denoising model that is basically parameter free, i.e. all model parameters are estimated directly from the noisy image. Moreover, we use Chambolle-Pock's primal dual method as well as the Douglas-Rachford method for the new models. For the latter one has to solve large discretizations of partial differential equations. We propose to do this in an inexact manner using the preconditioned conjugate gradients method and derive preconditioners for this. Numerical experiments show that the resulting method has good denoising properties and also that preconditioning does increase convergence speed significantly. Finally we analyze the duality gap of different formulations of the TGV denoising problem and derive a simple stopping criterion.

An extended Perona-Malik model based on probabilistic models

The Perona-Malik model has been very successful at restoring images from noisy input. In this paper, we reinterpret the Perona-Malik model in the language of Gaussian scale mixtures and derive some extensions of the model. Specifically, we show that the expectation-maximization (EM) algorithm applied to Gaussian scale mixtures leads to the lagged-diffusivity algorithm for computing stationary points of the Perona-Malik diffusion equations. Moreover, we show how mean field approximations to these Gaussian scale mixtures lead to a modification of the lagged-diffusivity algorithm that better captures the uncertainties in the restoration. Since this modification can be hard to compute in practice we propose relaxations to the mean field objective to make the algorithm computationally feasible. Our numerical experiments show that this modified lagged-diffusivity algorithm often performs better at restoring textured areas and fuzzy edges than the unmodified algorithm. As a second application of the Gaussian scale mixture framework, we show how an efficient sampling procedure can be obtained for the probabilistic model, making the computation of the conditional mean and other expectations algorithmically feasible. Again, the resulting algorithm has a strong resemblance to the lagged-diffusivity algorithm. Finally, we show that a probabilistic version of the Mumford-Shah segementation model can be obtained in the same framework with a discrete edge-prior.

An inertial forward-backward algorithm for monotone inclusions

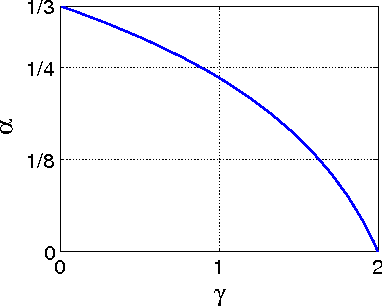
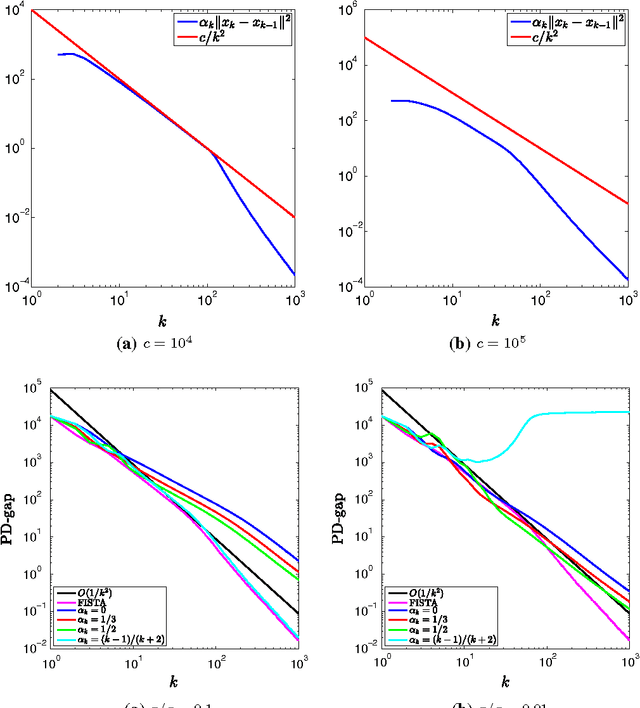
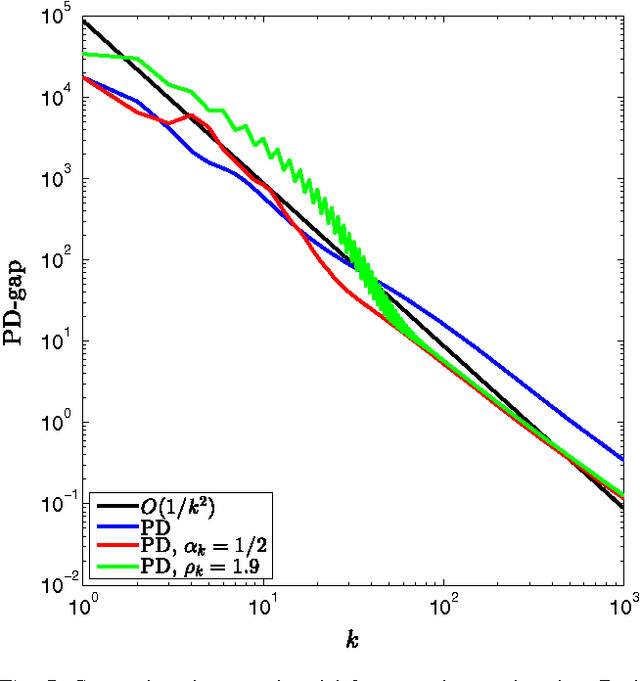
In this paper, we propose an inertial forward backward splitting algorithm to compute a zero of the sum of two monotone operators, with one of the two operators being co-coercive. The algorithm is inspired by the accelerated gradient method of Nesterov, but can be applied to a much larger class of problems including convex-concave saddle point problems and general monotone inclusions. We prove convergence of the algorithm in a Hilbert space setting and show that several recently proposed first-order methods can be obtained as special cases of the general algorithm. Numerical results show that the proposed algorithm converges faster than existing methods, while keeping the computational cost of each iteration basically unchanged.

Imaging with Kantorovich-Rubinstein discrepancy

We propose the use of the Kantorovich-Rubinstein norm from optimal transport in imaging problems. In particular, we discuss a variational regularisation model endowed with a Kantorovich-Rubinstein discrepancy term and total variation regularization in the context of image denoising and cartoon-texture decomposition. We point out connections of this approach to several other recently proposed methods such as total generalized variation and norms capturing oscillating patterns. We also show that the respective optimization problem can be turned into a convex-concave saddle point problem with simple constraints and hence, can be solved by standard tools. Numerical examples exhibit interesting features and favourable performance for denoising and cartoon-texture decomposition.

A sparse Kaczmarz solver and a linearized Bregman method for online compressed sensing

An algorithmic framework to compute sparse or minimal-TV solutions of linear systems is proposed. The framework includes both the Kaczmarz method and the linearized Bregman method as special cases and also several new methods such as a sparse Kaczmarz solver. The algorithmic framework has a variety of applications and is especially useful for problems in which the linear measurements are slow and expensive to obtain. We present examples for online compressed sensing, TV tomographic reconstruction and radio interferometry.

The Linearized Bregman Method via Split Feasibility Problems: Analysis and Generalizations

The linearized Bregman method is a method to calculate sparse solutions to systems of linear equations. We formulate this problem as a split feasibility problem, propose an algorithmic framework based on Bregman projections and prove a general convergence result for this framework. Convergence of the linearized Bregman method will be obtained as a special case. Our approach also allows for several generalizations such as other objective functions, incremental iterations, incorporation of non-gaussian noise models or box constraints.

Image sequence interpolation using optimal control

The problem of the generation of an intermediate image between two given images in an image sequence is considered. The problem is formulated as an optimal control problem governed by a transport equation. This approach bears similarities with the Horn \& Schunck method for optical flow calculation but in fact the model is quite different. The images are modelled in $BV$ and an analysis of solutions of transport equations with values in $BV$ is included. Moreover, the existence of optimal controls is proven and necessary conditions are derived. Finally, two algorithms are given and numerical results are compared with existing methods. The new method is competitive with state-of-the-art methods and even outperforms several existing methods.