Development of Automated Neural Network Prediction for Echocardiographic Left ventricular Ejection Fraction

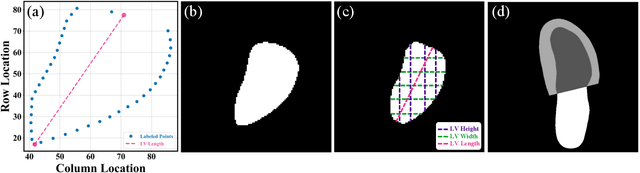
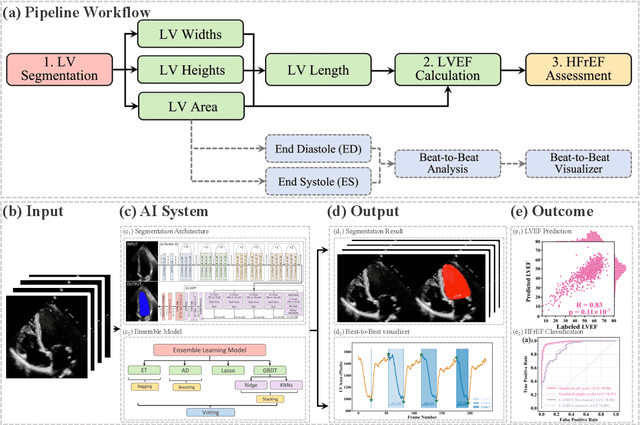
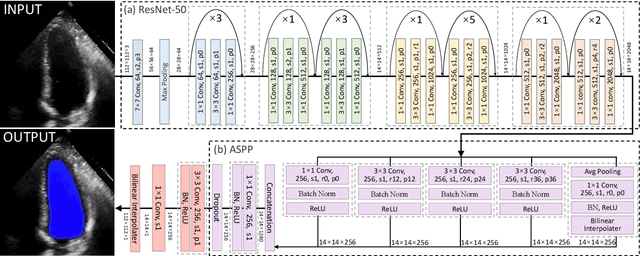
The echocardiographic measurement of left ventricular ejection fraction (LVEF) is fundamental to the diagnosis and classification of patients with heart failure (HF). In order to quantify LVEF automatically and accurately, this paper proposes a new pipeline method based on deep neural networks and ensemble learning. Within the pipeline, an Atrous Convolutional Neural Network (ACNN) was first trained to segment the left ventricle (LV), before employing the area-length formulation based on the ellipsoid single-plane model to calculate LVEF values. This formulation required inputs of LV area, derived from segmentation using an improved Jeffrey's method, as well as LV length, derived from a novel ensemble learning model. To further improve the pipeline's accuracy, an automated peak detection algorithm was used to identify end-diastolic and end-systolic frames, avoiding issues with human error. Subsequently, single-beat LVEF values were averaged across all cardiac cycles to obtain the final LVEF. This method was developed and internally validated in an open-source dataset containing 10,030 echocardiograms. The Pearson's correlation coefficient was 0.83 for LVEF prediction compared to expert human analysis (p<0.001), with a subsequent area under the receiver operator curve (AUROC) of 0.98 (95% confidence interval 0.97 to 0.99) for categorisation of HF with reduced ejection (HFrEF; LVEF<40%). In an external dataset with 200 echocardiograms, this method achieved an AUC of 0.90 (95% confidence interval 0.88 to 0.91) for HFrEF assessment. This study demonstrates that an automated neural network-based calculation of LVEF is comparable to expert clinicians performing time-consuming, frame-by-frame manual evaluation of cardiac systolic function.

Fourier-Net+: Leveraging Band-Limited Representation for Efficient 3D Medical Image Registration

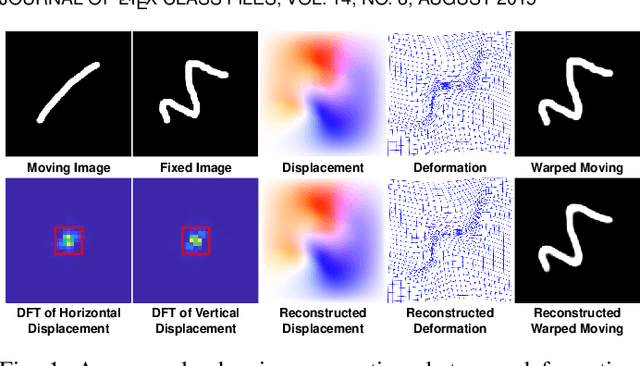
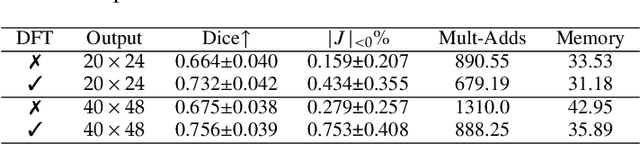
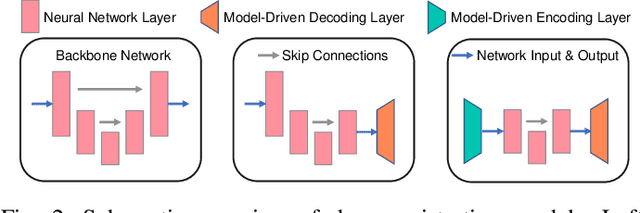
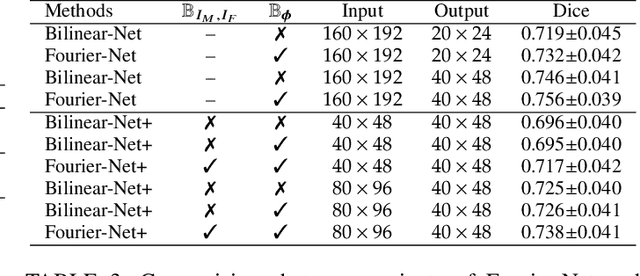
U-Net style networks are commonly utilized in unsupervised image registration to predict dense displacement fields, which for high-resolution volumetric image data is a resource-intensive and time-consuming task. To tackle this challenge, we first propose Fourier-Net, which replaces the costly U-Net style expansive path with a parameter-free model-driven decoder. Instead of directly predicting a full-resolution displacement field, our Fourier-Net learns a low-dimensional representation of the displacement field in the band-limited Fourier domain which our model-driven decoder converts to a full-resolution displacement field in the spatial domain. Expanding upon Fourier-Net, we then introduce Fourier-Net+, which additionally takes the band-limited spatial representation of the images as input and further reduces the number of convolutional layers in the U-Net style network's contracting path. Finally, to enhance the registration performance, we propose a cascaded version of Fourier-Net+. We evaluate our proposed methods on three datasets, on which our proposed Fourier-Net and its variants achieve comparable results with current state-of-the art methods, while exhibiting faster inference speeds, lower memory footprint, and fewer multiply-add operations. With such small computational cost, our Fourier-Net+ enables the efficient training of large-scale 3D registration on low-VRAM GPUs. Our code is publicly available at \url{https://github.com/xi-jia/Fourier-Net}.

Nesterov Accelerated ADMM for Fast Diffeomorphic Image Registration

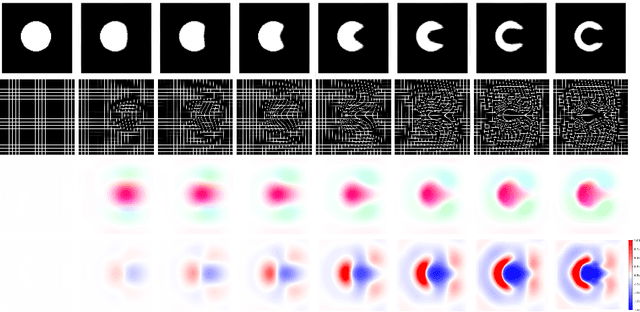
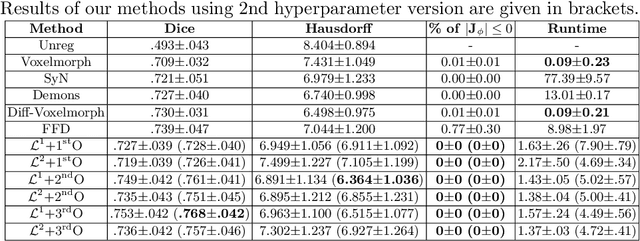
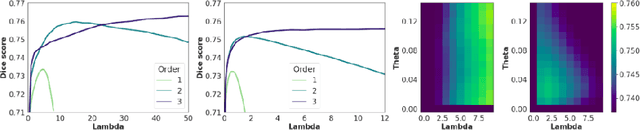
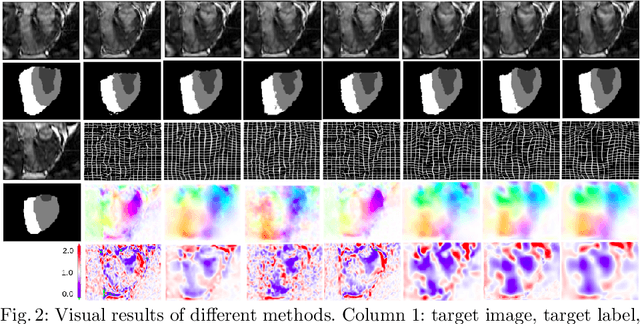
Deterministic approaches using iterative optimisation have been historically successful in diffeomorphic image registration (DiffIR). Although these approaches are highly accurate, they typically carry a significant computational burden. Recent developments in stochastic approaches based on deep learning have achieved sub-second runtimes for DiffIR with competitive registration accuracy, offering a fast alternative to conventional iterative methods. In this paper, we attempt to reduce this difference in speed whilst retaining the performance advantage of iterative approaches in DiffIR. We first propose a simple iterative scheme that functionally composes intermediate non-stationary velocity fields to handle large deformations in images whilst guaranteeing diffeomorphisms in the resultant deformation. We then propose a convex optimisation model that uses a regularisation term of arbitrary order to impose smoothness on these velocity fields and solve this model with a fast algorithm that combines Nesterov gradient descent and the alternating direction method of multipliers (ADMM). Finally, we leverage the computational power of GPU to implement this accelerated ADMM solver on a 3D cardiac MRI dataset, further reducing runtime to less than 2 seconds. In addition to producing strictly diffeomorphic deformations, our methods outperform both state-of-the-art deep learning-based and iterative DiffIR approaches in terms of dice and Hausdorff scores, with speed approaching the inference time of deep learning-based methods.