Karina Bunting
Nesterov Accelerated ADMM for Fast Diffeomorphic Image Registration
Sep 26, 2021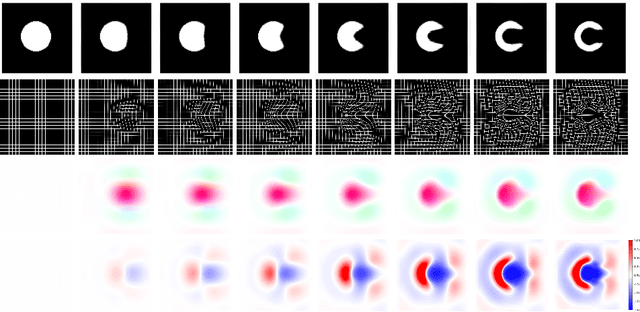
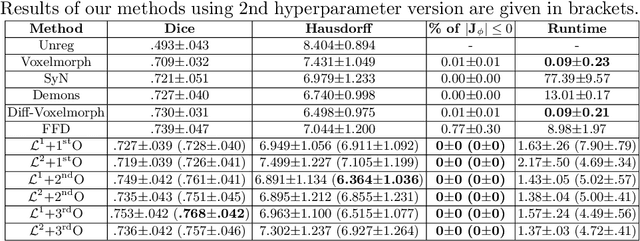
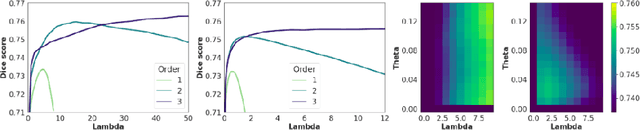
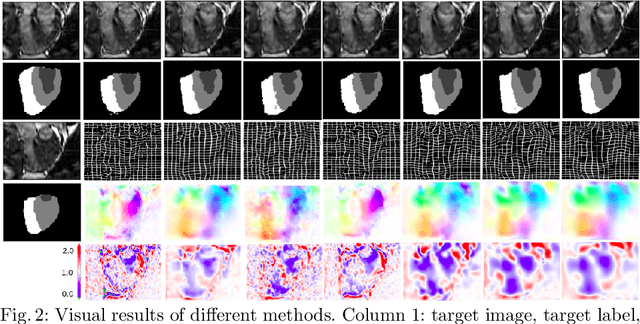
Abstract:Deterministic approaches using iterative optimisation have been historically successful in diffeomorphic image registration (DiffIR). Although these approaches are highly accurate, they typically carry a significant computational burden. Recent developments in stochastic approaches based on deep learning have achieved sub-second runtimes for DiffIR with competitive registration accuracy, offering a fast alternative to conventional iterative methods. In this paper, we attempt to reduce this difference in speed whilst retaining the performance advantage of iterative approaches in DiffIR. We first propose a simple iterative scheme that functionally composes intermediate non-stationary velocity fields to handle large deformations in images whilst guaranteeing diffeomorphisms in the resultant deformation. We then propose a convex optimisation model that uses a regularisation term of arbitrary order to impose smoothness on these velocity fields and solve this model with a fast algorithm that combines Nesterov gradient descent and the alternating direction method of multipliers (ADMM). Finally, we leverage the computational power of GPU to implement this accelerated ADMM solver on a 3D cardiac MRI dataset, further reducing runtime to less than 2 seconds. In addition to producing strictly diffeomorphic deformations, our methods outperform both state-of-the-art deep learning-based and iterative DiffIR approaches in terms of dice and Hausdorff scores, with speed approaching the inference time of deep learning-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge