Generalized Proof-Number Monte-Carlo Tree Search

This paper presents Generalized Proof-Number Monte-Carlo Tree Search: a generalization of recently proposed combinations of Proof-Number Search (PNS) with Monte-Carlo Tree Search (MCTS), which use (dis)proof numbers to bias UCB1-based Selection strategies towards parts of the search that are expected to be easily (dis)proven. We propose three core modifications of prior combinations of PNS with MCTS. First, we track proof numbers per player. This reduces code complexity in the sense that we no longer need disproof numbers, and generalizes the technique to be applicable to games with more than two players. Second, we propose and extensively evaluate different methods of using proof numbers to bias the selection strategy, achieving strong performance with strategies that are simpler to implement and compute. Third, we merge our technique with Score Bounded MCTS, enabling the algorithm to prove and leverage upper and lower bounds on scores - as opposed to only proving wins or not-wins. Experiments demonstrate substantial performance increases, reaching the range of 80% for 8 out of the 11 tested board games.

Environment Descriptions for Usability and Generalisation in Reinforcement Learning

The majority of current reinforcement learning (RL) research involves training and deploying agents in environments that are implemented by engineers in general-purpose programming languages and more advanced frameworks such as CUDA or JAX. This makes the application of RL to novel problems of interest inaccessible to small organisations or private individuals with insufficient engineering expertise. This position paper argues that, to enable more widespread adoption of RL, it is important for the research community to shift focus towards methodologies where environments are described in user-friendly domain-specific or natural languages. Aside from improving the usability of RL, such language-based environment descriptions may also provide valuable context and boost the ability of trained agents to generalise to unseen environments within the set of all environments that can be described in any language of choice.

Anytime Sequential Halving in Monte-Carlo Tree Search

Monte-Carlo Tree Search (MCTS) typically uses multi-armed bandit (MAB) strategies designed to minimize cumulative regret, such as UCB1, as its selection strategy. However, in the root node of the search tree, it is more sensible to minimize simple regret. Previous work has proposed using Sequential Halving as selection strategy in the root node, as, in theory, it performs better with respect to simple regret. However, Sequential Halving requires a budget of iterations to be predetermined, which is often impractical. This paper proposes an anytime version of the algorithm, which can be halted at any arbitrary time and still return a satisfactory result, while being designed such that it approximates the behavior of Sequential Halving. Empirical results in synthetic MAB problems and ten different board games demonstrate that the algorithm's performance is competitive with Sequential Halving and UCB1 (and their analogues in MCTS).

Exploring RL-based LLM Training for Formal Language Tasks with Programmed Rewards

Proximal Policy Optimization (PPO) is commonly used in Reinforcement Learning from Human Feedback to align large language models (LLMs) with downstream tasks. This paper investigates the feasibility of using PPO for direct reinforcement learning (RL) from explicitly programmed reward signals, as opposed to indirect learning from human feedback via an intermediary reward model. We focus on tasks expressed through formal languages, such as mathematics and programming, where explicit reward functions can be programmed to automatically assess the quality of generated outputs. We apply this approach to a sentiment alignment task, a simple arithmetic task, and a more complex game synthesis task. The sentiment alignment task replicates prior research and serves to validate our experimental setup. Our results show that pure RL-based training for the two formal language tasks is challenging, with success being limited even for the simple arithmetic task. We propose a novel batch-entropy regularization term to aid exploration, although training is not yet entirely stable. Our findings suggest that direct RL training of LLMs may be more suitable for relatively minor changes, such as alignment, than for learning new tasks altogether, even if an informative reward signal can be expressed programmatically.

GAVEL: Generating Games Via Evolution and Language Models

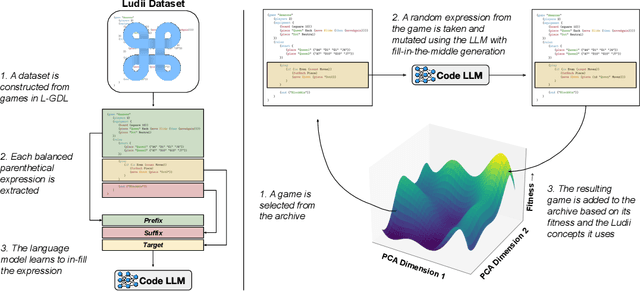
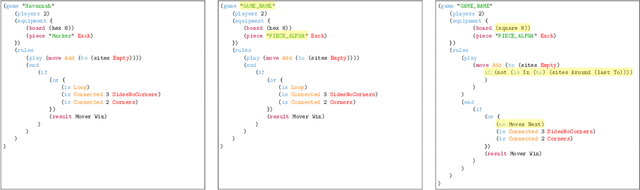
Automatically generating novel and interesting games is a complex task. Challenges include representing game rules in a computationally workable form, searching through the large space of potential games under most such representations, and accurately evaluating the originality and quality of previously unseen games. Prior work in automated game generation has largely focused on relatively restricted rule representations and relied on domain-specific heuristics. In this work, we explore the generation of novel games in the comparatively expansive Ludii game description language, which encodes the rules of over 1000 board games in a variety of styles and modes of play. We draw inspiration from recent advances in large language models and evolutionary computation in order to train a model that intelligently mutates and recombines games and mechanics expressed as code. We demonstrate both quantitatively and qualitatively that our approach is capable of generating new and interesting games, including in regions of the potential rules space not covered by existing games in the Ludii dataset. A sample of the generated games are available to play online through the Ludii portal.

Enhancements for Real-Time Monte-Carlo Tree Search in General Video Game Playing

General Video Game Playing (GVGP) is a field of Artificial Intelligence where agents play a variety of real-time video games that are unknown in advance. This limits the use of domain-specific heuristics. Monte-Carlo Tree Search (MCTS) is a search technique for game playing that does not rely on domain-specific knowledge. This paper discusses eight enhancements for MCTS in GVGP; Progressive History, N-Gram Selection Technique, Tree Reuse, Breadth-First Tree Initialization, Loss Avoidance, Novelty-Based Pruning, Knowledge-Based Evaluations, and Deterministic Game Detection. Some of these are known from existing literature, and are either extended or introduced in the context of GVGP, and some are novel enhancements for MCTS. Most enhancements are shown to provide statistically significant increases in win percentages when applied individually. When combined, they increase the average win percentage over sixty different games from 31.0% to 48.4% in comparison to a vanilla MCTS implementation, approaching a level that is competitive with the best agents of the GVG-AI competition in 2015.

Games of Knightian Uncertainty as AGI testbeds

Arguably, for the latter part of the late 20th and early 21st centuries, games have been seen as the drosophila of AI. Games are a set of exciting testbeds, whose solutions (in terms of identifying optimal players) would lead to machines that would possess some form of general intelligence, or at the very least help us gain insights toward building intelligent machines. Following impressive successes in traditional board games like Go, Chess, and Poker, but also video games like the Atari 2600 collection, it is clear that this is not the case. Games have been attacked successfully, but we are nowhere near AGI developments (or, as harsher critics might say, useful AI developments!). In this short vision paper, we argue that for game research to become again relevant to the AGI pathway, we need to be able to address \textit{Knightian uncertainty} in the context of games, i.e. agents need to be able to adapt to rapid changes in game rules on the fly with no warning, no previous data, and no model access.

Towards a Characterisation of Monte-Carlo Tree Search Performance in Different Games

Many enhancements to Monte-Carlo Tree Search (MCTS) have been proposed over almost two decades of general game playing and other artificial intelligence research. However, our ability to characterise and understand which variants work well or poorly in which games is still lacking. This paper describes work on an initial dataset that we have built to make progress towards such an understanding: 268,386 plays among 61 different agents across 1494 distinct games. We describe a preliminary analysis and work on training predictive models on this dataset, as well as lessons learned and future plans for a new and improved version of the dataset.

Proof Number Based Monte-Carlo Tree Search

This paper proposes a new game search algorithm, PN-MCTS, that combines Monte-Carlo Tree Search (MCTS) and Proof-Number Search (PNS). These two algorithms have been successfully applied for decision making in a range of domains. We define three areas where the additional knowledge provided by the proof and disproof numbers gathered in MCTS trees might be used: final move selection, solving subtrees, and the UCT formula. We test all possible combinations on different time settings, playing against vanilla UCT MCTS on several games: Lines of Action ($7$$\times$$7$ and $8$$\times$$8$), MiniShogi, Knightthrough, Awari, and Gomoku. Furthermore, we extend this new algorithm to properly address games with draws, like Awari, by adding an additional layer of PNS on top of the MCTS tree. The experiments show that PN-MCTS confidently outperforms MCTS in 5 out of 6 game domains (all except Gomoku), achieving win rates up to 96.2% for Lines of Action.

Measuring Board Game Distance

This paper presents a general approach for measuring distances between board games within the Ludii general game system. These distances are calculated using a previously published set of general board game concepts, each of which represents a common game idea or shared property. Our results compare and contrast two different measures of distance, highlighting the subjective nature of such metrics and discussing the different ways that they can be interpreted.