Generalized Proof-Number Monte-Carlo Tree Search

This paper presents Generalized Proof-Number Monte-Carlo Tree Search: a generalization of recently proposed combinations of Proof-Number Search (PNS) with Monte-Carlo Tree Search (MCTS), which use (dis)proof numbers to bias UCB1-based Selection strategies towards parts of the search that are expected to be easily (dis)proven. We propose three core modifications of prior combinations of PNS with MCTS. First, we track proof numbers per player. This reduces code complexity in the sense that we no longer need disproof numbers, and generalizes the technique to be applicable to games with more than two players. Second, we propose and extensively evaluate different methods of using proof numbers to bias the selection strategy, achieving strong performance with strategies that are simpler to implement and compute. Third, we merge our technique with Score Bounded MCTS, enabling the algorithm to prove and leverage upper and lower bounds on scores - as opposed to only proving wins or not-wins. Experiments demonstrate substantial performance increases, reaching the range of 80% for 8 out of the 11 tested board games.

Towards Explaining Monte-Carlo Tree Search by Using Its Enhancements

Typically, research on Explainable Artificial Intelligence (XAI) focuses on black-box models within the context of a general policy in a known, specific domain. This paper advocates for the need for knowledge-agnostic explainability applied to the subfield of XAI called Explainable Search, which focuses on explaining the choices made by intelligent search techniques. It proposes Monte-Carlo Tree Search (MCTS) enhancements as a solution to obtaining additional data and providing higher-quality explanations while remaining knowledge-free, and analyzes the most popular enhancements in terms of the specific types of explainability they introduce. So far, no other research has considered the explainability of MCTS enhancements. We present a proof-of-concept that demonstrates the advantages of utilizing enhancements.

Quantum Circuit Design using a Progressive Widening Monte Carlo Tree Search

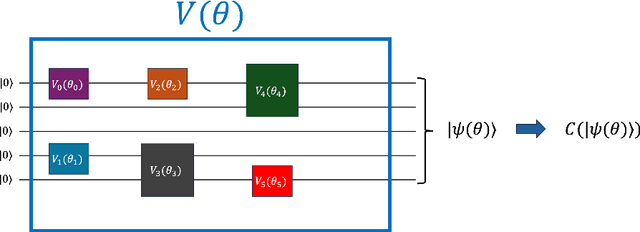
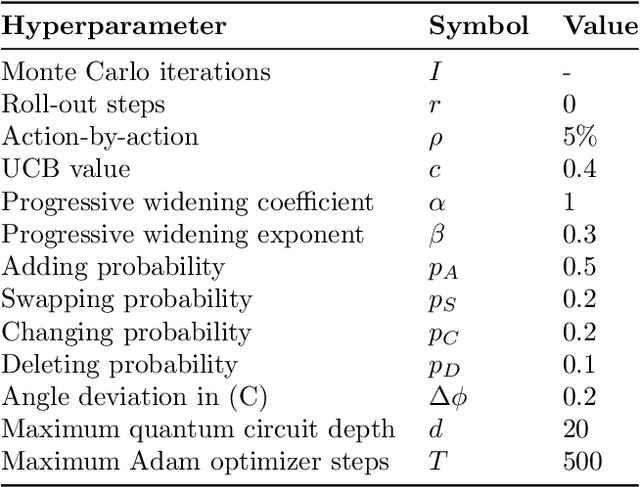
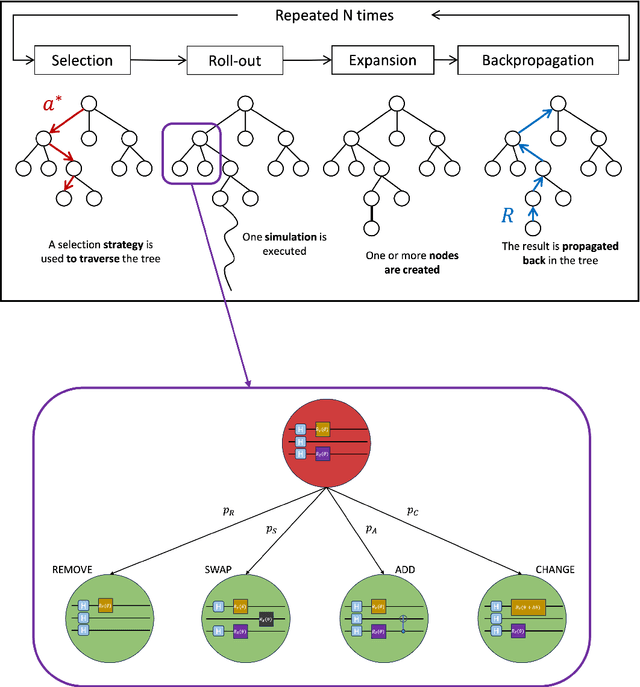
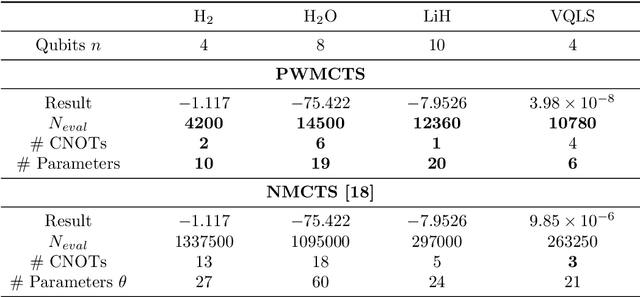
The performance of Variational Quantum Algorithms (VQAs) strongly depends on the choice of the parameterized quantum circuit to optimize. One of the biggest challenges in VQAs is designing quantum circuits tailored to the particular problem and to the quantum hardware. This article proposes a gradient-free Monte Carlo Tree Search (MCTS) technique to automate the process of quantum circuit design. It introduces a novel formulation of the action space based on a sampling scheme and a progressive widening technique to explore the space dynamically. When testing our MCTS approach on the domain of random quantum circuits, MCTS approximates unstructured circuits under different values of stabilizer R\'enyi entropy. It turns out that MCTS manages to approximate the benchmark quantum states independently from their degree of nonstabilizerness. Next, our technique exhibits robustness across various application domains, including quantum chemistry and systems of linear equations. Compared to previous MCTS research, our technique reduces the number of quantum circuit evaluations by a factor of 10 to 100 while achieving equal or better results. In addition, the resulting quantum circuits have up to three times fewer CNOT gates.

Environment Descriptions for Usability and Generalisation in Reinforcement Learning

The majority of current reinforcement learning (RL) research involves training and deploying agents in environments that are implemented by engineers in general-purpose programming languages and more advanced frameworks such as CUDA or JAX. This makes the application of RL to novel problems of interest inaccessible to small organisations or private individuals with insufficient engineering expertise. This position paper argues that, to enable more widespread adoption of RL, it is important for the research community to shift focus towards methodologies where environments are described in user-friendly domain-specific or natural languages. Aside from improving the usability of RL, such language-based environment descriptions may also provide valuable context and boost the ability of trained agents to generalise to unseen environments within the set of all environments that can be described in any language of choice.

Anytime Sequential Halving in Monte-Carlo Tree Search

Monte-Carlo Tree Search (MCTS) typically uses multi-armed bandit (MAB) strategies designed to minimize cumulative regret, such as UCB1, as its selection strategy. However, in the root node of the search tree, it is more sensible to minimize simple regret. Previous work has proposed using Sequential Halving as selection strategy in the root node, as, in theory, it performs better with respect to simple regret. However, Sequential Halving requires a budget of iterations to be predetermined, which is often impractical. This paper proposes an anytime version of the algorithm, which can be halted at any arbitrary time and still return a satisfactory result, while being designed such that it approximates the behavior of Sequential Halving. Empirical results in synthetic MAB problems and ten different board games demonstrate that the algorithm's performance is competitive with Sequential Halving and UCB1 (and their analogues in MCTS).

Enhancements for Real-Time Monte-Carlo Tree Search in General Video Game Playing

General Video Game Playing (GVGP) is a field of Artificial Intelligence where agents play a variety of real-time video games that are unknown in advance. This limits the use of domain-specific heuristics. Monte-Carlo Tree Search (MCTS) is a search technique for game playing that does not rely on domain-specific knowledge. This paper discusses eight enhancements for MCTS in GVGP; Progressive History, N-Gram Selection Technique, Tree Reuse, Breadth-First Tree Initialization, Loss Avoidance, Novelty-Based Pruning, Knowledge-Based Evaluations, and Deterministic Game Detection. Some of these are known from existing literature, and are either extended or introduced in the context of GVGP, and some are novel enhancements for MCTS. Most enhancements are shown to provide statistically significant increases in win percentages when applied individually. When combined, they increase the average win percentage over sixty different games from 31.0% to 48.4% in comparison to a vanilla MCTS implementation, approaching a level that is competitive with the best agents of the GVG-AI competition in 2015.

Towards a Characterisation of Monte-Carlo Tree Search Performance in Different Games

Many enhancements to Monte-Carlo Tree Search (MCTS) have been proposed over almost two decades of general game playing and other artificial intelligence research. However, our ability to characterise and understand which variants work well or poorly in which games is still lacking. This paper describes work on an initial dataset that we have built to make progress towards such an understanding: 268,386 plays among 61 different agents across 1494 distinct games. We describe a preliminary analysis and work on training predictive models on this dataset, as well as lessons learned and future plans for a new and improved version of the dataset.

Proof Number Based Monte-Carlo Tree Search

This paper proposes a new game search algorithm, PN-MCTS, that combines Monte-Carlo Tree Search (MCTS) and Proof-Number Search (PNS). These two algorithms have been successfully applied for decision making in a range of domains. We define three areas where the additional knowledge provided by the proof and disproof numbers gathered in MCTS trees might be used: final move selection, solving subtrees, and the UCT formula. We test all possible combinations on different time settings, playing against vanilla UCT MCTS on several games: Lines of Action ($7$$\times$$7$ and $8$$\times$$8$), MiniShogi, Knightthrough, Awari, and Gomoku. Furthermore, we extend this new algorithm to properly address games with draws, like Awari, by adding an additional layer of PNS on top of the MCTS tree. The experiments show that PN-MCTS confidently outperforms MCTS in 5 out of 6 game domains (all except Gomoku), achieving win rates up to 96.2% for Lines of Action.

Monte-Carlo Tree-Search for Leveraging Performance of Blackbox Job-Shop Scheduling Heuristics

In manufacturing, the production is often done on out-of-the-shelf manufacturing lines, whose underlying scheduling heuristics are not known due to the intellectual property. We consider such a setting with a black-box job-shop system and an unknown scheduling heuristic that, for a given permutation of jobs, schedules the jobs for the black-box job-shop with the goal of minimizing the makespan. Here, the jobs need to enter the job-shop in the given order of the permutation, but may take different paths within the job shop, which depends on the black-box heuristic. The performance of the black-box heuristic depends on the order of the jobs, and the natural problem for the manufacturer is to find an optimum ordering of the jobs. Facing a real-world scenario as described above, we engineer the Monte-Carlo tree-search for finding a close-to-optimum ordering of jobs. To cope with a large solutions-space in planning scenarios, a hierarchical Monte-Carlo tree search (H-MCTS) is proposed based on abstraction of jobs. On synthetic and real-life problems, H-MCTS with integrated abstraction significantly outperforms pure heuristic-based techniques as well as other Monte-Carlo search variants. We furthermore show that, by modifying the evaluation metric in H-MCTS, it is possible to achieve other optimization objectives than what the scheduling heuristics are designed for -- e.g., minimizing the total completion time instead of the makespan. Our experimental observations have been also validated in real-life cases, and our H-MCTS approach has been implemented in a production plant's controller.

Combining Monte-Carlo Tree Search with Proof-Number Search

Proof-Number Search (PNS) and Monte-Carlo Tree Search (MCTS) have been successfully applied for decision making in a range of games. This paper proposes a new approach called PN-MCTS that combines these two tree-search methods by incorporating the concept of proof and disproof numbers into the UCT formula of MCTS. Experimental results demonstrate that PN-MCTS outperforms basic MCTS in several games including Lines of Action, MiniShogi, Knightthrough, and Awari, achieving win rates up to 94.0%.