Towards Explaining Monte-Carlo Tree Search by Using Its Enhancements

Typically, research on Explainable Artificial Intelligence (XAI) focuses on black-box models within the context of a general policy in a known, specific domain. This paper advocates for the need for knowledge-agnostic explainability applied to the subfield of XAI called Explainable Search, which focuses on explaining the choices made by intelligent search techniques. It proposes Monte-Carlo Tree Search (MCTS) enhancements as a solution to obtaining additional data and providing higher-quality explanations while remaining knowledge-free, and analyzes the most popular enhancements in terms of the specific types of explainability they introduce. So far, no other research has considered the explainability of MCTS enhancements. We present a proof-of-concept that demonstrates the advantages of utilizing enhancements.

VFL-RPS: Relevant Participant Selection in Vertical Federated Learning

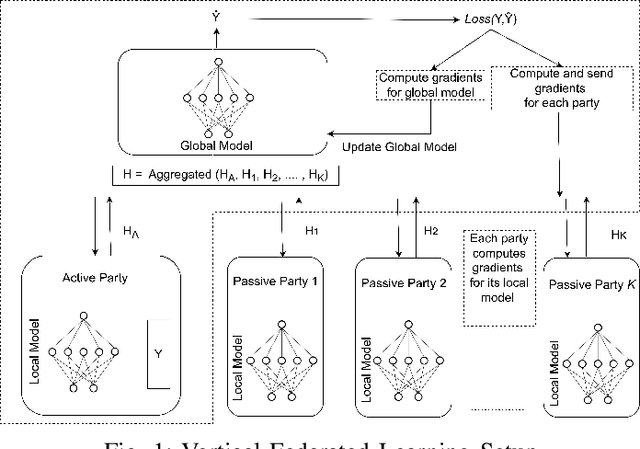
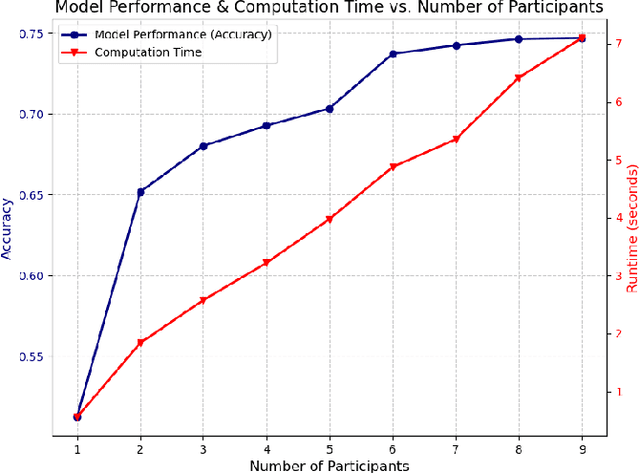
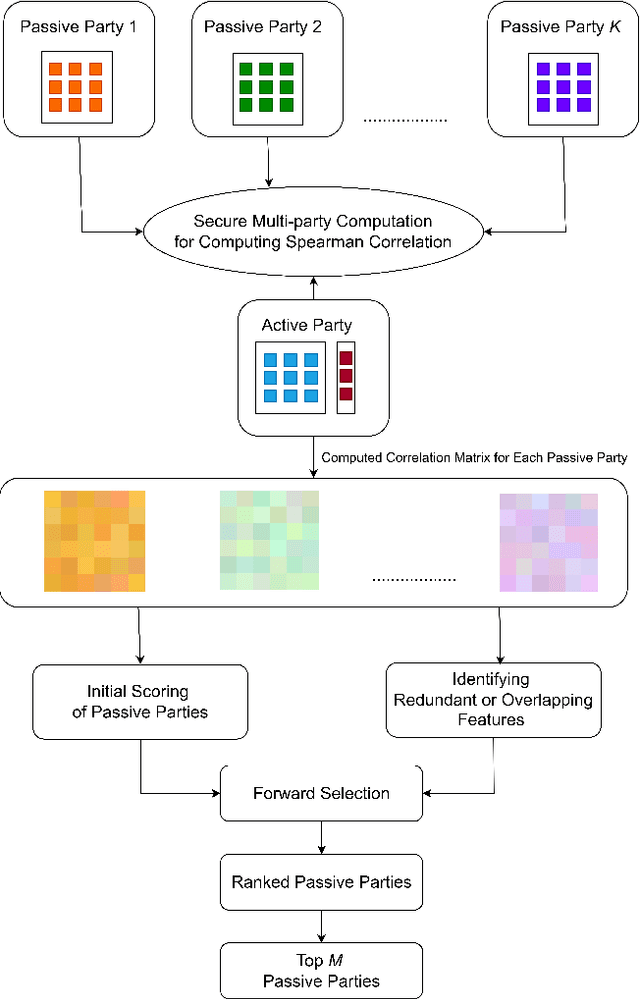
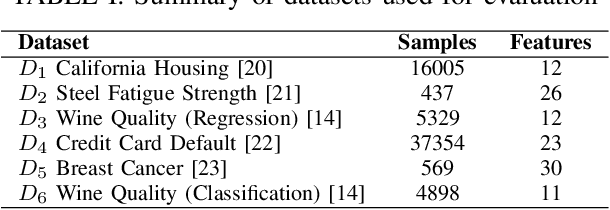
Federated Learning (FL) allows collaboration between different parties, while ensuring that the data across these parties is not shared. However, not every collaboration is helpful in terms of the resulting model performance. Therefore, it is an important challenge to select the correct participants in a collaboration. As it currently stands, most of the efforts in participant selection in the literature have focused on Horizontal Federated Learning (HFL), which assumes that all features are the same across all participants, disregarding the possibility of different features across participants which is captured in Vertical Federated Learning (VFL). To close this gap in the literature, we propose a novel method VFL-RPS for participant selection in VFL, as a pre-training step. We have tested our method on several data sets performing both regression and classification tasks, showing that our method leads to comparable results as using all data by only selecting a few participants. In addition, we show that our method outperforms existing methods for participant selection in VFL.

Hierarchical Blockmodelling for Knowledge Graphs

In this paper, we investigate the use of probabilistic graphical models, specifically stochastic blockmodels, for the purpose of hierarchical entity clustering on knowledge graphs. These models, seldom used in the Semantic Web community, decompose a graph into a set of probability distributions. The parameters of these distributions are then inferred allowing for their subsequent sampling to generate a random graph. In a non-parametric setting, this allows for the induction of hierarchical clusterings without prior constraints on the hierarchy's structure. Specifically, this is achieved by the integration of the Nested Chinese Restaurant Process and the Stick Breaking Process into the generative model. In this regard, we propose a model leveraging such integration and derive a collapsed Gibbs sampling scheme for its inference. To aid in understanding, we describe the steps in this derivation and provide an implementation for the sampler. We evaluate our model on synthetic and real-world datasets and quantitatively compare against benchmark models. We further evaluate our results qualitatively and find that our model is capable of inducing coherent cluster hierarchies in small scale settings. The work presented in this paper provides the first step for the further application of stochastic blockmodels for knowledge graphs on a larger scale. We conclude the paper with potential avenues for future work on more scalable inference schemes.

Empirical Capacity Model for Self-Attention Neural Networks

Large pretrained self-attention neural networks, or transformers, have been very successful in various tasks recently. The performance of a model on a given task depends on its ability to memorize and generalize the training data. Large transformer models, which may have billions of parameters, in theory have a huge capacity to memorize content. However, the current algorithms for the optimization fall short of the theoretical capacity, and the capacity is also highly dependent on the content. In this paper, we focus on the memory capacity of these models obtained using common training algorithms and synthetic training data. Based on the results, we derive an empirical capacity model (ECM) for a generic transformer. The ECM can be used to design task-specific transformer models with an optimal number of parameters in cases where the target memorization capability of the task can be defined.

Incentive Allocation in Vertical Federated Learning Based on Bankruptcy Problem

Vertical federated learning (VFL) is a promising approach for collaboratively training machine learning models using private data partitioned vertically across different parties. Ideally in a VFL setting, the active party (party possessing features of samples with labels) benefits by improving its machine learning model through collaboration with some passive parties (parties possessing additional features of the same samples without labels) in a privacy preserving manner. However, motivating passive parties to participate in VFL can be challenging. In this paper, we focus on the problem of allocating incentives to the passive parties by the active party based on their contributions to the VFL process. We formulate this problem as a variant of the Nucleolus game theory concept, known as the Bankruptcy Problem, and solve it using the Talmud's division rule. We evaluate our proposed method on synthetic and real-world datasets and show that it ensures fairness and stability in incentive allocation among passive parties who contribute their data to the federated model. Additionally, we compare our method to the existing solution of calculating Shapley values and show that our approach provides a more efficient solution with fewer computations.

Vertical Federated Learning: A Structured Literature Review

Federated Learning (FL) has emerged as a promising distributed learning paradigm with an added advantage of data privacy. With the growing interest in having collaboration among data owners, FL has gained significant attention of organizations. The idea of FL is to enable collaborating participants train machine learning (ML) models on decentralized data without breaching privacy. In simpler words, federated learning is the approach of ``bringing the model to the data, instead of bringing the data to the mode''. Federated learning, when applied to data which is partitioned vertically across participants, is able to build a complete ML model by combining local models trained only using the data with distinct features at the local sites. This architecture of FL is referred to as vertical federated learning (VFL), which differs from the conventional FL on horizontally partitioned data. As VFL is different from conventional FL, it comes with its own issues and challenges. In this paper, we present a structured literature review discussing the state-of-the-art approaches in VFL. Additionally, the literature review highlights the existing solutions to challenges in VFL and provides potential research directions in this domain.

Towards Federated Clustering: A Federated Fuzzy $c$-Means Algorithm (FFCM)

Federated Learning (FL) is a setting where multiple parties with distributed data collaborate in training a joint Machine Learning (ML) model while keeping all data local at the parties. Federated clustering is an area of research within FL that is concerned with grouping together data that is globally similar while keeping all data local. We describe how this area of research can be of interest in itself, or how it helps addressing issues like non-independently-identically-distributed (i.i.d.) data in supervised FL frameworks. The focus of this work, however, is an extension of the federated fuzzy $c$-means algorithm to the FL setting (FFCM) as a contribution towards federated clustering. We propose two methods to calculate global cluster centers and evaluate their behaviour through challenging numerical experiments. We observe that one of the methods is able to identify good global clusters even in challenging scenarios, but also acknowledge that many challenges remain open.