Hierarchical Blockmodelling for Knowledge Graphs

In this paper, we investigate the use of probabilistic graphical models, specifically stochastic blockmodels, for the purpose of hierarchical entity clustering on knowledge graphs. These models, seldom used in the Semantic Web community, decompose a graph into a set of probability distributions. The parameters of these distributions are then inferred allowing for their subsequent sampling to generate a random graph. In a non-parametric setting, this allows for the induction of hierarchical clusterings without prior constraints on the hierarchy's structure. Specifically, this is achieved by the integration of the Nested Chinese Restaurant Process and the Stick Breaking Process into the generative model. In this regard, we propose a model leveraging such integration and derive a collapsed Gibbs sampling scheme for its inference. To aid in understanding, we describe the steps in this derivation and provide an implementation for the sampler. We evaluate our model on synthetic and real-world datasets and quantitatively compare against benchmark models. We further evaluate our results qualitatively and find that our model is capable of inducing coherent cluster hierarchies in small scale settings. The work presented in this paper provides the first step for the further application of stochastic blockmodels for knowledge graphs on a larger scale. We conclude the paper with potential avenues for future work on more scalable inference schemes.

Path Based Hierarchical Clustering on Knowledge Graphs

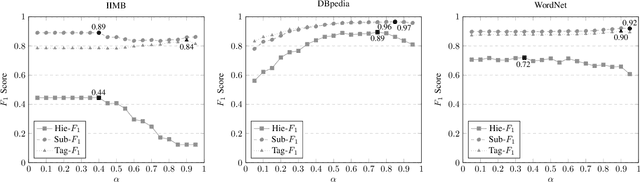
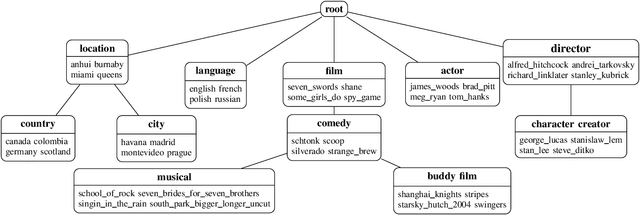
Knowledge graphs have emerged as a widely adopted medium for storing relational data, making methods for automatically reasoning with them highly desirable. In this paper, we present a novel approach for inducing a hierarchy of subject clusters, building upon our earlier work done in taxonomy induction. Our method first constructs a tag hierarchy before assigning subjects to clusters on this hierarchy. We quantitatively demonstrate our method's ability to induce a coherent cluster hierarchy on three real-world datasets.

Fragmentation Coagulation Based Mixed Membership Stochastic Blockmodel

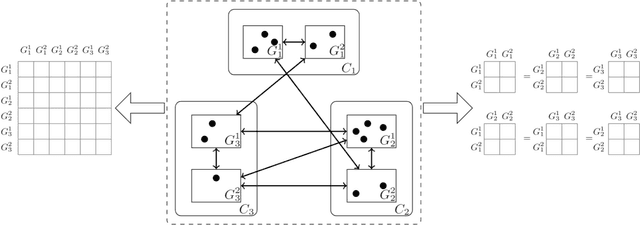
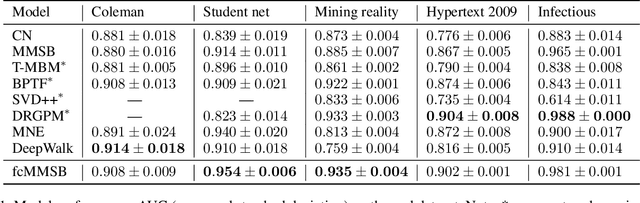
The Mixed-Membership Stochastic Blockmodel~(MMSB) is proposed as one of the state-of-the-art Bayesian relational methods suitable for learning the complex hidden structure underlying the network data. However, the current formulation of MMSB suffers from the following two issues: (1), the prior information~(e.g. entities' community structural information) can not be well embedded in the modelling; (2), community evolution can not be well described in the literature. Therefore, we propose a non-parametric fragmentation coagulation based Mixed Membership Stochastic Blockmodel (fcMMSB). Our model performs entity-based clustering to capture the community information for entities and linkage-based clustering to derive the group information for links simultaneously. Besides, the proposed model infers the network structure and models community evolution, manifested by appearances and disappearances of communities, using the discrete fragmentation coagulation process (DFCP). By integrating the community structure with the group compatibility matrix we derive a generalized version of MMSB. An efficient Gibbs sampling scheme with Polya Gamma (PG) approach is implemented for posterior inference. We validate our model on synthetic and real world data.

Identification of Pleonastic It Using the Web

In a significant minority of cases, certain pronouns, especially the pronoun it, can be used without referring to any specific entity. This phenomenon of pleonastic pronoun usage poses serious problems for systems aiming at even a shallow understanding of natural language texts. In this paper, a novel approach is proposed to identify such uses of it: the extrapositional cases are identified using a series of queries against the web, and the cleft cases are identified using a simple set of syntactic rules. The system is evaluated with four sets of news articles containing 679 extrapositional cases as well as 78 cleft constructs. The identification results are comparable to those obtained by human efforts.