Fragmentation Coagulation Based Mixed Membership Stochastic Blockmodel
Paper and Code
Jan 17, 2020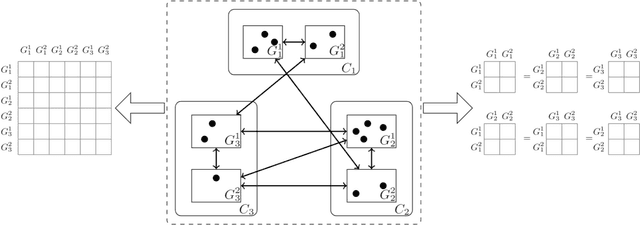
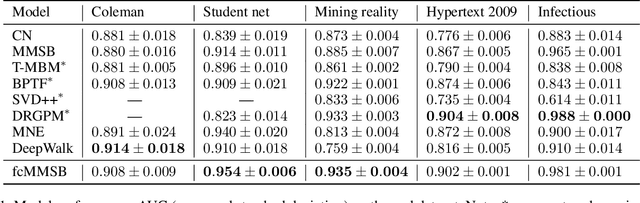
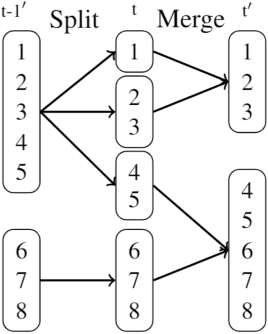
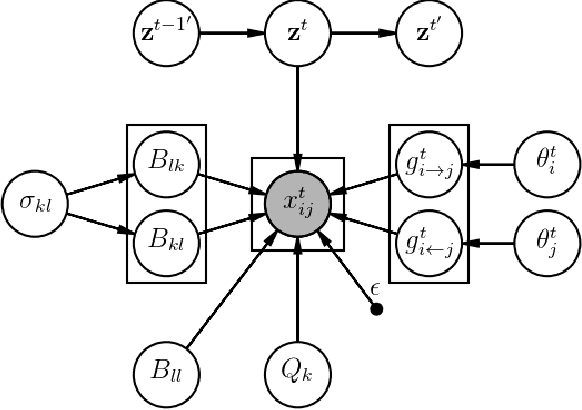
The Mixed-Membership Stochastic Blockmodel~(MMSB) is proposed as one of the state-of-the-art Bayesian relational methods suitable for learning the complex hidden structure underlying the network data. However, the current formulation of MMSB suffers from the following two issues: (1), the prior information~(e.g. entities' community structural information) can not be well embedded in the modelling; (2), community evolution can not be well described in the literature. Therefore, we propose a non-parametric fragmentation coagulation based Mixed Membership Stochastic Blockmodel (fcMMSB). Our model performs entity-based clustering to capture the community information for entities and linkage-based clustering to derive the group information for links simultaneously. Besides, the proposed model infers the network structure and models community evolution, manifested by appearances and disappearances of communities, using the discrete fragmentation coagulation process (DFCP). By integrating the community structure with the group compatibility matrix we derive a generalized version of MMSB. An efficient Gibbs sampling scheme with Polya Gamma (PG) approach is implemented for posterior inference. We validate our model on synthetic and real world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge