State-Reification Networks: Improving Generalization by Modeling the Distribution of Hidden Representations

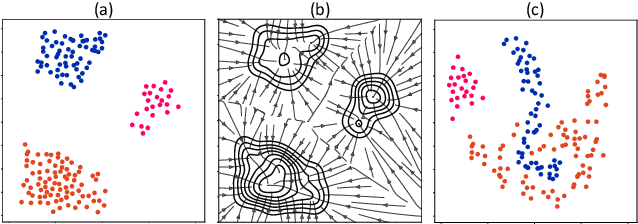
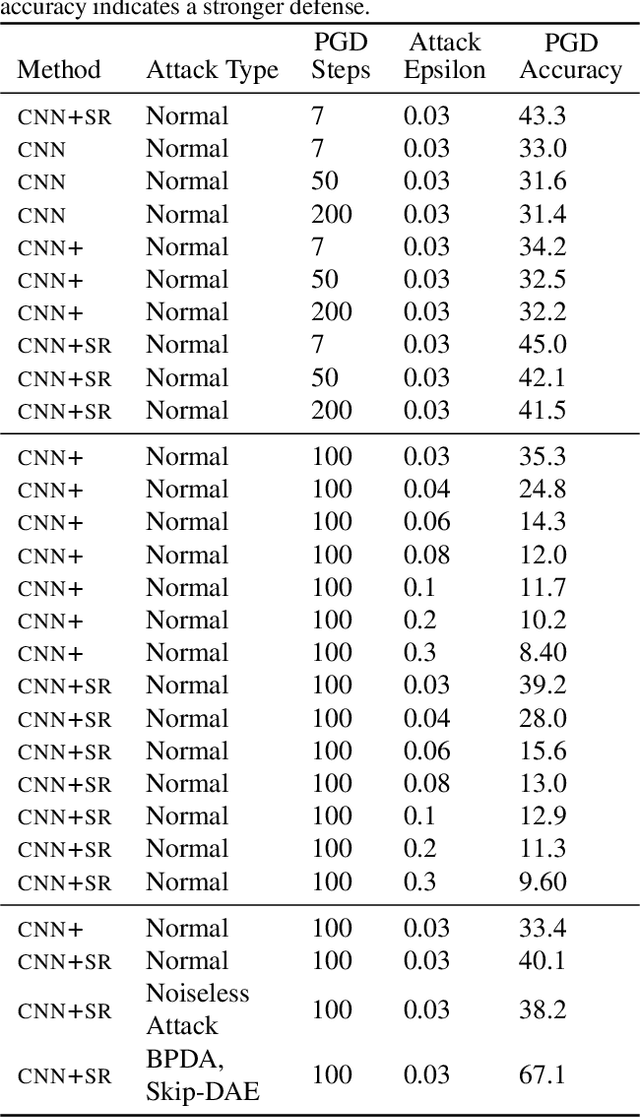
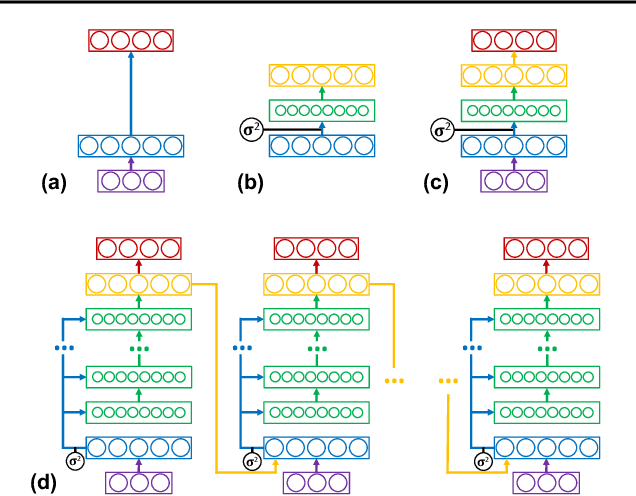
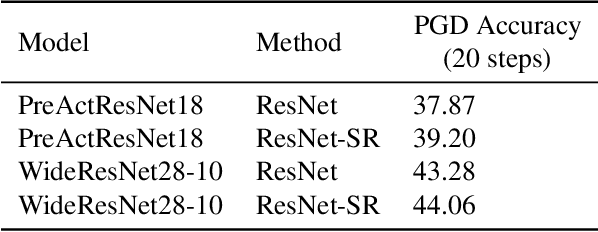
Machine learning promises methods that generalize well from finite labeled data. However, the brittleness of existing neural net approaches is revealed by notable failures, such as the existence of adversarial examples that are misclassified despite being nearly identical to a training example, or the inability of recurrent sequence-processing nets to stay on track without teacher forcing. We introduce a method, which we refer to as \emph{state reification}, that involves modeling the distribution of hidden states over the training data and then projecting hidden states observed during testing toward this distribution. Our intuition is that if the network can remain in a familiar manifold of hidden space, subsequent layers of the net should be well trained to respond appropriately. We show that this state-reification method helps neural nets to generalize better, especially when labeled data are sparse, and also helps overcome the challenge of achieving robust generalization with adversarial training.

State-Denoised Recurrent Neural Networks

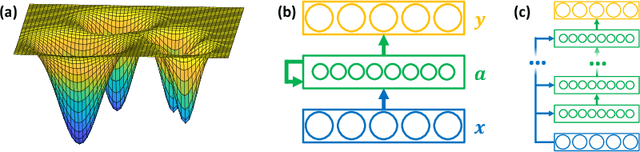
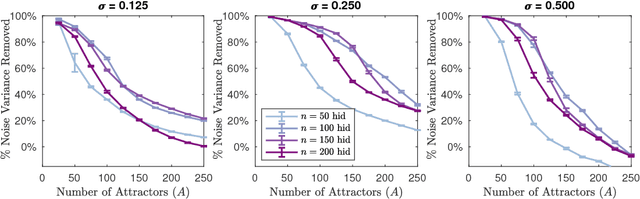
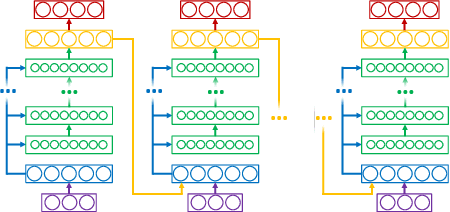
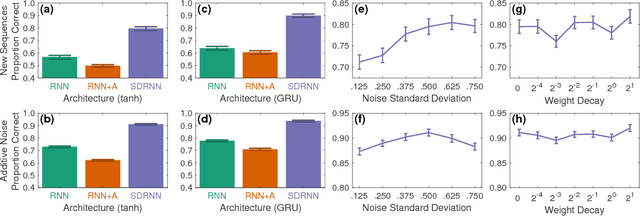
Recurrent neural networks (RNNs) are difficult to train on sequence processing tasks, not only because input noise may be amplified through feedback, but also because any inaccuracy in the weights has similar consequences as input noise. We describe a method for denoising the hidden state during training to achieve more robust representations thereby improving generalization performance. Attractor dynamics are incorporated into the hidden state to `clean up' representations at each step of a sequence. The attractor dynamics are trained through an auxillary denoising loss to recover previously experienced hidden states from noisy versions of those states. This state-denoised recurrent neural network {SDRNN} performs multiple steps of internal processing for each external sequence step. On a range of tasks, we show that the SDRNN outperforms a generic RNN as well as a variant of the SDRNN with attractor dynamics on the hidden state but without the auxillary loss. We argue that attractor dynamics---and corresponding connectivity constraints---are an essential component of the deep learning arsenal and should be invoked not only for recurrent networks but also for improving deep feedforward nets and intertask transfer.

Discrete Event, Continuous Time RNNs

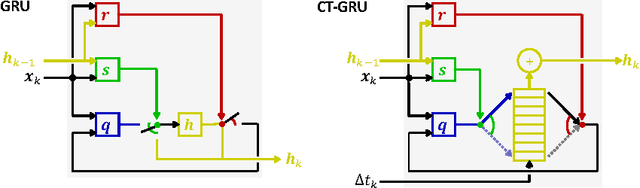
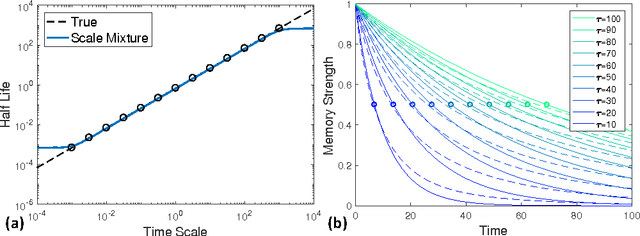
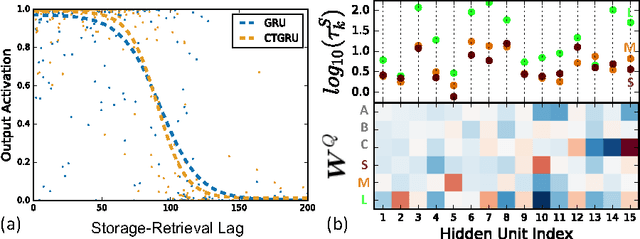
We investigate recurrent neural network architectures for event-sequence processing. Event sequences, characterized by discrete observations stamped with continuous-valued times of occurrence, are challenging due to the potentially wide dynamic range of relevant time scales as well as interactions between time scales. We describe four forms of inductive bias that should benefit architectures for event sequences: temporal locality, position and scale homogeneity, and scale interdependence. We extend the popular gated recurrent unit (GRU) architecture to incorporate these biases via intrinsic temporal dynamics, obtaining a continuous-time GRU. The CT-GRU arises by interpreting the gates of a GRU as selecting a time scale of memory, and the CT-GRU generalizes the GRU by incorporating multiple time scales of memory and performing context-dependent selection of time scales for information storage and retrieval. Event time-stamps drive decay dynamics of the CT-GRU, whereas they serve as generic additional inputs to the GRU. Despite the very different manner in which the two models consider time, their performance on eleven data sets we examined is essentially identical. Our surprising results point both to the robustness of GRU and LSTM architectures for handling continuous time, and to the potency of incorporating continuous dynamics into neural architectures.