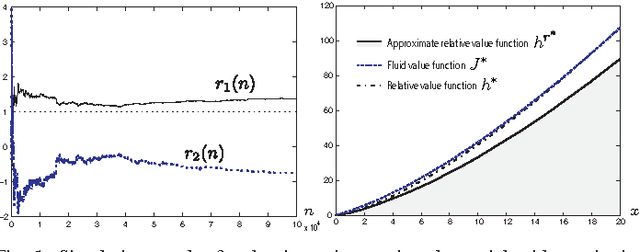
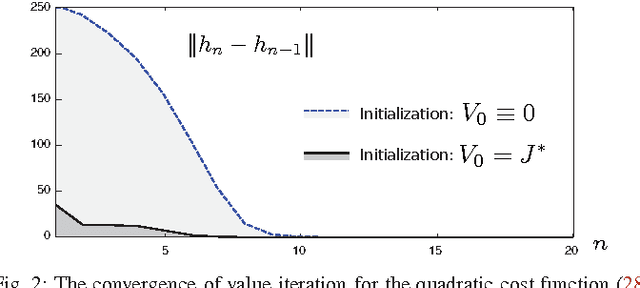
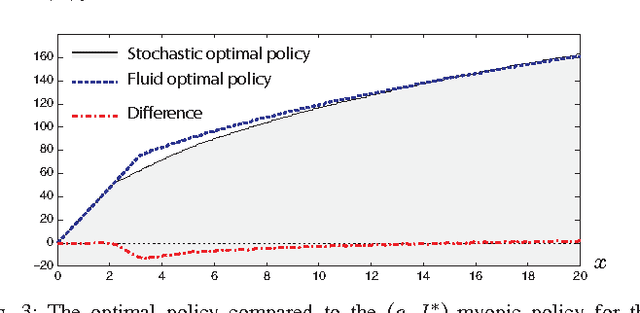
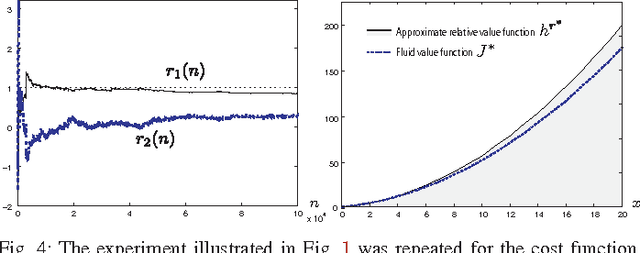
Approximate dynamic programming using fluid and diffusion approximations with applications to power management

Neuro-dynamic programming is a class of powerful techniques for approximating the solution to dynamic programming equations. In their most computationally attractive formulations, these techniques provide the approximate solution only within a prescribed finite-dimensional function class. Thus, the question that always arises is how should the function class be chosen? The goal of this paper is to propose an approach using the solutions to associated fluid and diffusion approximations. In order to illustrate this approach, the paper focuses on an application to dynamic speed scaling for power management in computer processors.

Universal and Composite Hypothesis Testing via Mismatched Divergence

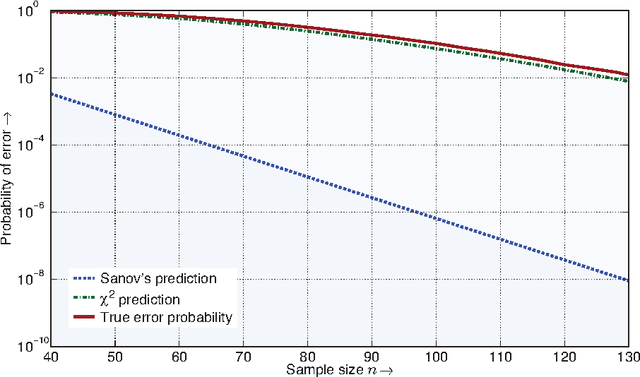
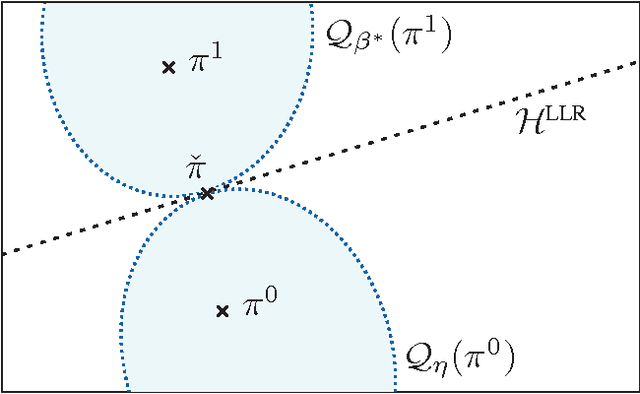
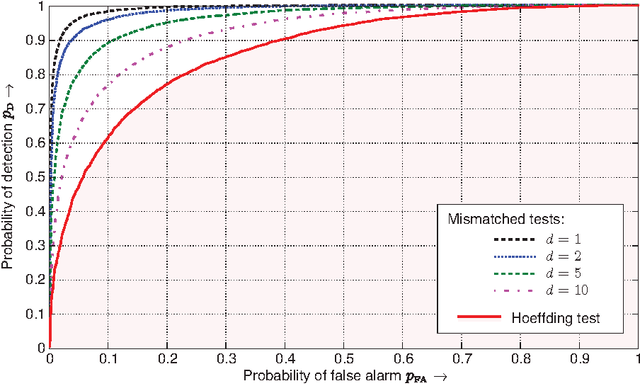
For the universal hypothesis testing problem, where the goal is to decide between the known null hypothesis distribution and some other unknown distribution, Hoeffding proposed a universal test in the nineteen sixties. Hoeffding's universal test statistic can be written in terms of Kullback-Leibler (K-L) divergence between the empirical distribution of the observations and the null hypothesis distribution. In this paper a modification of Hoeffding's test is considered based on a relaxation of the K-L divergence test statistic, referred to as the mismatched divergence. The resulting mismatched test is shown to be a generalized likelihood-ratio test (GLRT) for the case where the alternate distribution lies in a parametric family of the distributions characterized by a finite dimensional parameter, i.e., it is a solution to the corresponding composite hypothesis testing problem. For certain choices of the alternate distribution, it is shown that both the Hoeffding test and the mismatched test have the same asymptotic performance in terms of error exponents. A consequence of this result is that the GLRT is optimal in differentiating a particular distribution from others in an exponential family. It is also shown that the mismatched test has a significant advantage over the Hoeffding test in terms of finite sample size performance. This advantage is due to the difference in the asymptotic variances of the two test statistics under the null hypothesis. In particular, the variance of the K-L divergence grows linearly with the alphabet size, making the test impractical for applications involving large alphabet distributions. The variance of the mismatched divergence on the other hand grows linearly with the dimension of the parameter space, and can hence be controlled through a prudent choice of the function class defining the mismatched divergence.

Feature Extraction for Universal Hypothesis Testing via Rank-constrained Optimization

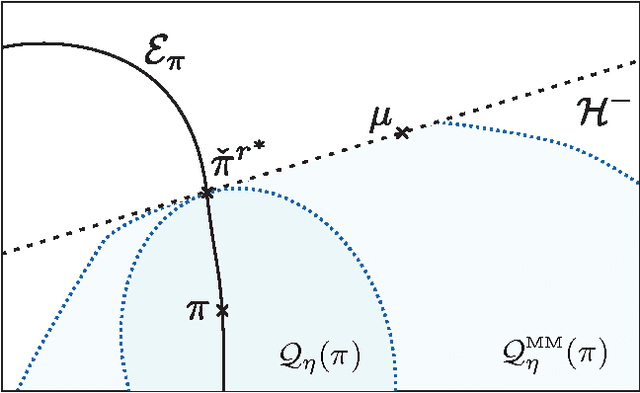
This paper concerns the construction of tests for universal hypothesis testing problems, in which the alternate hypothesis is poorly modeled and the observation space is large. The mismatched universal test is a feature-based technique for this purpose. In prior work it is shown that its finite-observation performance can be much better than the (optimal) Hoeffding test, and good performance depends crucially on the choice of features. The contributions of this paper include: 1) We obtain bounds on the number of \epsilon distinguishable distributions in an exponential family. 2) This motivates a new framework for feature extraction, cast as a rank-constrained optimization problem. 3) We obtain a gradient-based algorithm to solve the rank-constrained optimization problem and prove its local convergence.