Approximate dynamic programming using fluid and diffusion approximations with applications to power management
Paper and Code
Jul 09, 2013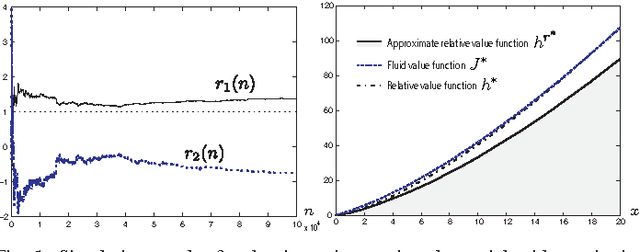
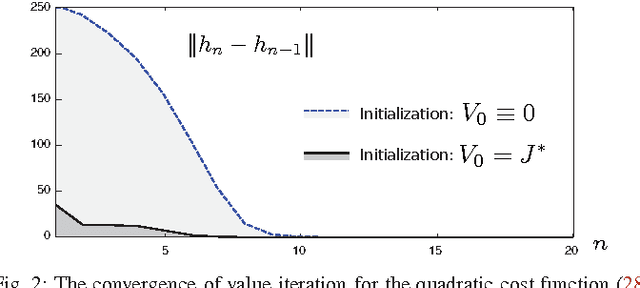
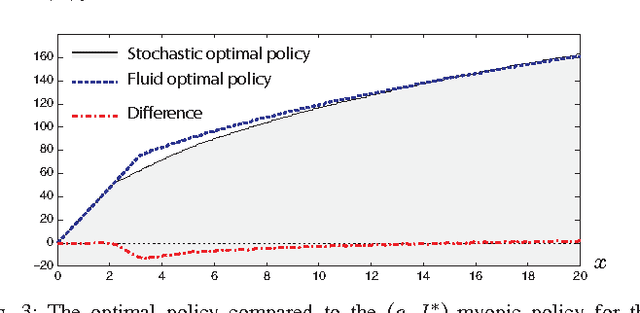
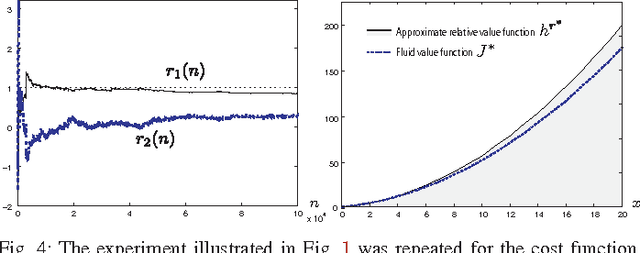
Neuro-dynamic programming is a class of powerful techniques for approximating the solution to dynamic programming equations. In their most computationally attractive formulations, these techniques provide the approximate solution only within a prescribed finite-dimensional function class. Thus, the question that always arises is how should the function class be chosen? The goal of this paper is to propose an approach using the solutions to associated fluid and diffusion approximations. In order to illustrate this approach, the paper focuses on an application to dynamic speed scaling for power management in computer processors.
* Submitted to SIAM Journal on Control and Optimization (SICON), July
2013
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge