Dimensionality Reduction of Affine Variational Inequalities Using Random Projections

We present a method for dimensionality reduction of an affine variational inequality (AVI) defined over a compact feasible region. Centered around the Johnson Lindenstrauss lemma, our method is a randomized algorithm that produces with high probability an approximate solution for the given AVI by solving a lower-dimensional AVI. The algorithm allows the lower dimension to be chosen based on the quality of approximation desired. The algorithm can also be used as a subroutine in an exact algorithm for generating an initial point close to the solution. The lower-dimensional AVI is obtained by appropriately projecting the original AVI on a randomly chosen subspace. The lower-dimensional AVI is solved using standard solvers and from this solution an approximate solution to the original AVI is recovered through an inexpensive process. Our numerical experiments corroborate the theoretical results and validate that the algorithm provides a good approximation at low dimensions and substantial savings in time for an exact solution.

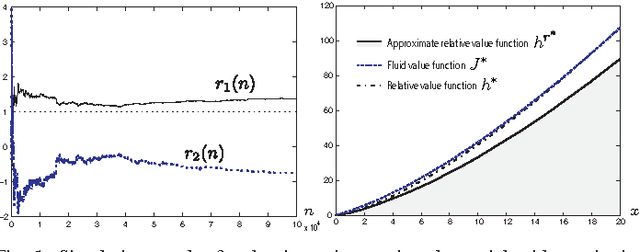
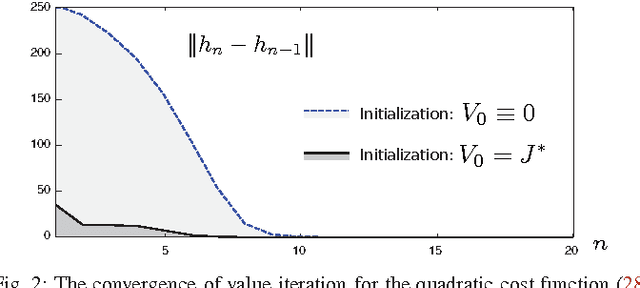
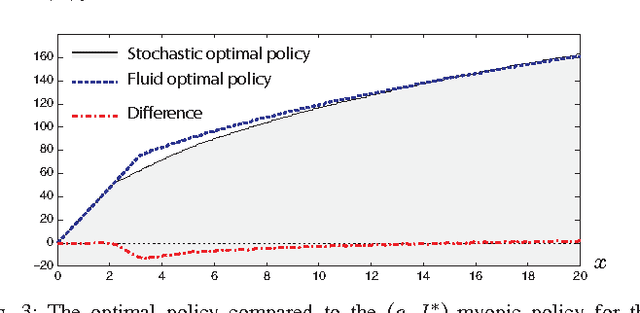
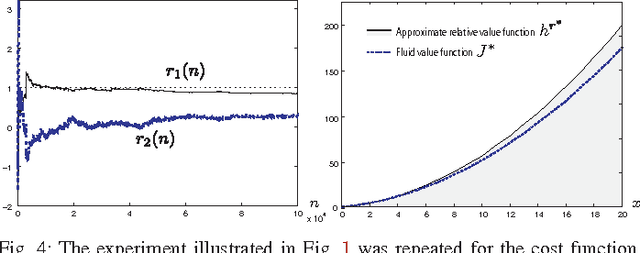
Approximate dynamic programming using fluid and diffusion approximations with applications to power management

Neuro-dynamic programming is a class of powerful techniques for approximating the solution to dynamic programming equations. In their most computationally attractive formulations, these techniques provide the approximate solution only within a prescribed finite-dimensional function class. Thus, the question that always arises is how should the function class be chosen? The goal of this paper is to propose an approach using the solutions to associated fluid and diffusion approximations. In order to illustrate this approach, the paper focuses on an application to dynamic speed scaling for power management in computer processors.